AVL树
什么是AVL树
AVL(Adelson-Velsky 和 Landis)树,是带有平衡条件的二叉查找树, 这个平衡条件必须要容易保持,并且它保证树的深度是\(O(LogN)\).
一颗AVL树是其每个节点的左右子树节点高度最多差1的二叉查找树。
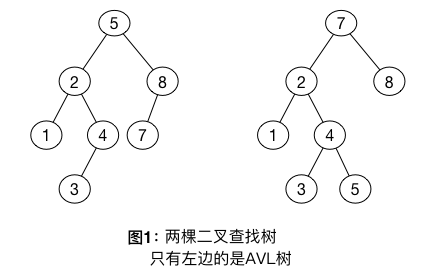
平衡条件
我门上面说,一颗AVL树是其每个节点的左右子树节点高度最多差1的二叉查找树。 左右子树的高度最多差1便是AVL树的平衡条件。
当进行插入操作时,我们需要更新通往根节点的所有节点的平衡信息。 而插入操作隐含困难的原因在于,可能会破坏AVL树的特性 (例如,考虑将6插入到图1的AVL树中将会破坏节点为8的平衡条件)。 如果发生这种情形,那么就要考虑在插入完成之后重新回复节点的平衡信息。 事实上,总可以通过对树进行简单的修正得到,我们称其为旋转(ratation).
在插入以后,只有那些从插入点到根节点的平衡条件可能变化, 因为只有这些节点的字数可能发生变化。当我们沿着这条路路径行进到根节点, 可以发现一个节点它的新平衡破坏了AVL树的特性。我们需要在这个节点重新平衡这棵树。
我们把必须重新平衡的节点叫做\(α\)。因为平衡条件是高度最多相差1, 那么出现不平衡就是\(α\)点的高度相差为2。容易看出这种不平衡可能出现在下面这四种情况下:
- 对\(α\)的左儿子的左子树进行一次插入
- 对\(α\)的左儿子的右子树进行一次插入
- 对\(α\)的右儿子的左子树进行一次插入
- 对\(α\)的右儿子的右子树进行一次插入
1和4,2和3 是关于α点的镜像对称。因此理论上讲只有两种情况,当然编程上还是四种情况。
第一种情况是插入发生在外边的情况(即左-左的情况或者右-右的情况), 该情况是通过对树的一次单旋转来完成操作。
第二种情况是插入发生在内部的情形(即左-右的情况或者右-左的情况), 该情况通过稍微复杂点的双旋转操作来处理。
单旋转
下图显示了单旋转如何调整情形1。旋转前的图在左边,旋转后的图在右边。
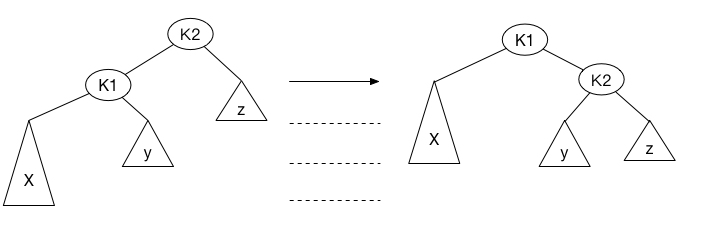
让我们来分析具体的做法。节点\(K2\)不满足平衡条件, 因为它的左子树比右子树深两层(图中的虚线表示树的各层).
为使树恢复平衡,我们把节点\(X\)向上移一层,并把Z像下移一层, 为此我们重新安排节点以形成一颗等价的树。如上图的右边部分。 抽象的形容就是,把把树想象成一棵柔软灵活的树,抓住子节点\(K1\), 闭上眼睛使劲的摇动它,这样由于重力的作用,\(K1\)就变成了新的根。 二叉树的性质告诉我们,在原树中\(K2 > K1\),这样在新树中,\(K2\)变成了\(K1\)的右儿子, \(Y\)变成了\(K2\)的左子树,而\(X\)、\(Z\)依然是\(K1\)的左子树和\(K2\)的右子树。
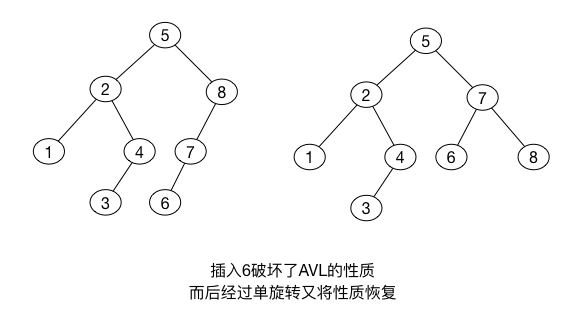
让我们演示一个更长的例子,假设从初始的空的AVL树开始依次插入\(3\)、\(2\)、\(1\), 然后再依次插入\(4-7\).
在插入关键字\(1\)的时候第一个问题就出现了,AVL性质在根处被破坏, 我们在根和其左儿子之间施加单旋转操作来修正问题。下图是旋转之前和之后的两棵树。
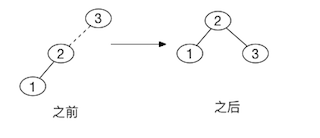
图中虚线连接的两个节点,它们是旋转的主体。下面我们插入关键字\(4\)这没有问题, 在我们插入关键字\(5\)的时候,问题又出现了,平衡条件在关键字\(3\)处被破坏, 而通过单旋转再次将问题修复。
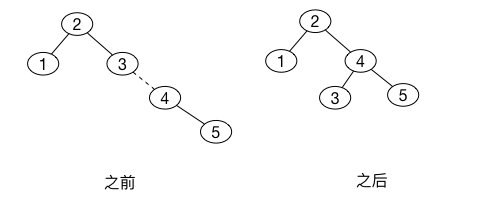
接下来插入\(6\),平衡条件在根节点处被打破,因此我们在根处, 在\(2\)、\(4\)之间施加一次单旋转操作。
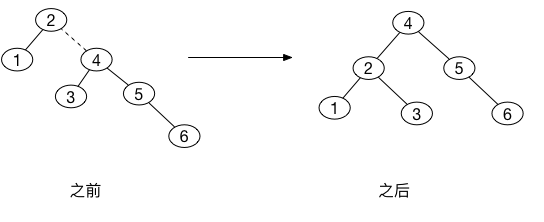
我们插入最后的关键字\(7\),它导致另外的旋转。
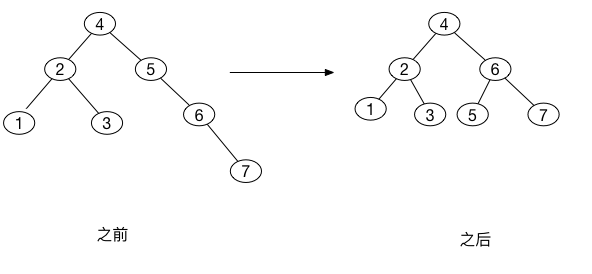
双旋转
单旋转对情形\(2\)、\(3\)无效愿因在于子树\(Y\)太深。单旋转没有降低它的深度。
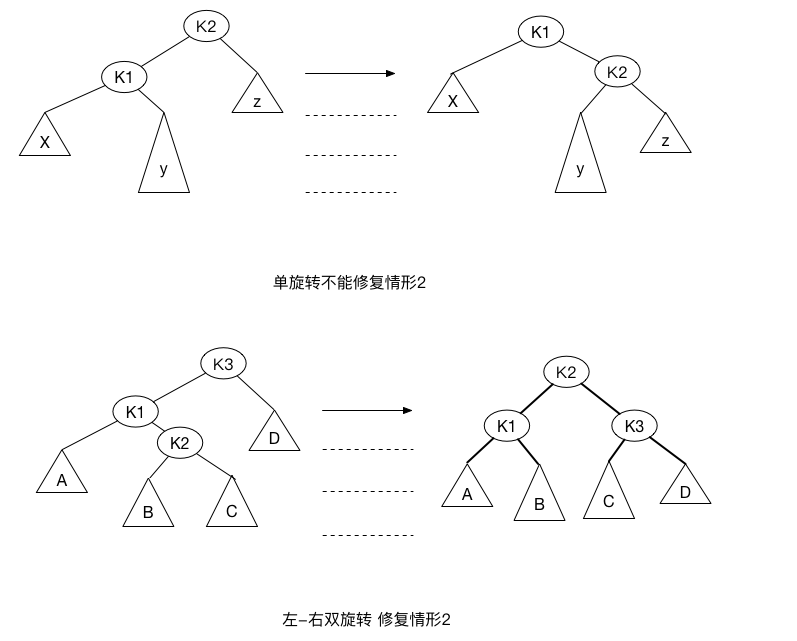
对于子树\(Y\)我们可以假设他有一个根和两棵子树(对应上图的\(K2\)、\(B\)、\(C\))。
为了平衡期间,我们不能再把\(K3\)当成根了, 而如上图所示\(K3\)和\(K1\)之间旋转又解决不了问题,唯一的选择是把\(K2\)当成根, 这迫\(K1\)成为\(K2\)的左子树,\(K3\)成为\(K1\)的右子树,而\(K2\)的左子树成为\(K1\)的右子树, \(K2\)的右子树成为\(K3\)的左子树。容易看出最后得到的树满足AVL树的特征。
我们继续在前面例子的基础上以倒序插入\(10-16\),接着插入\(8\),再插入\(9\)。 插入\(16\)很容易这并不破坏树的平衡,插入\(15\)会引起节点\(7\)处的高度不平衡, 这属于情形\(3\),需要通过右-左双旋转来解决。如图:
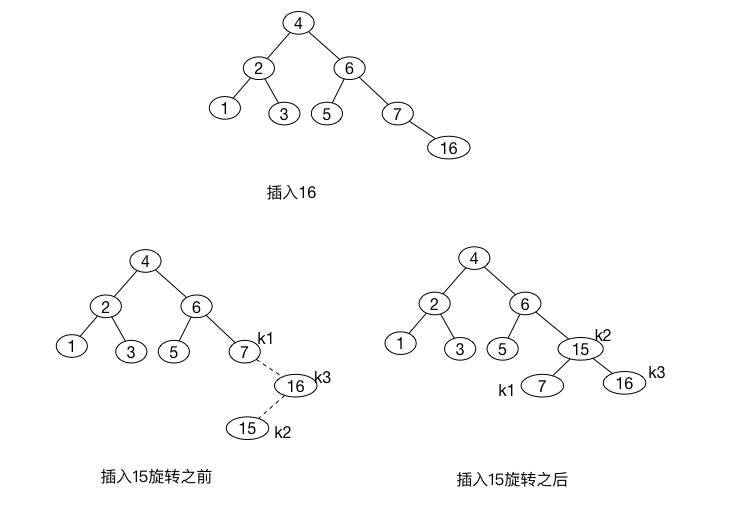
下面我们来插入\(14\),它也需要一个双旋转。此时修复树的旋转还是右-左双旋转
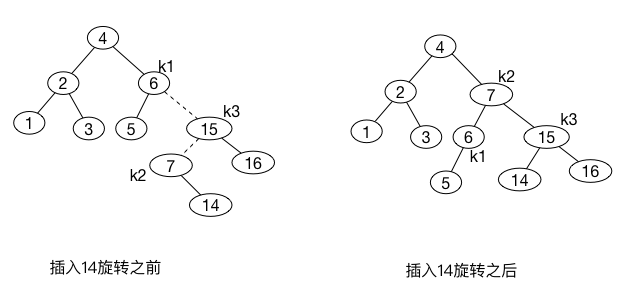
如果现在插入\(13\)那么在根处就会出现不平衡,由于\(13\)不在\(4-7\)之间, 我们知道只要一次单旋转就行.
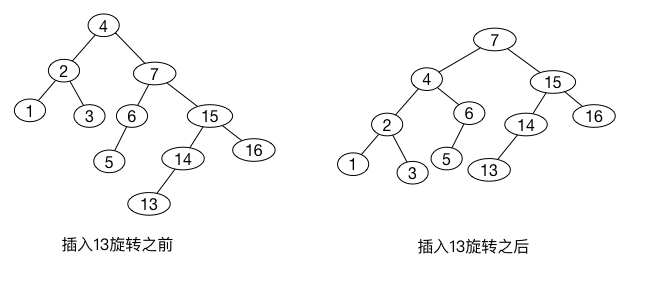
插入\(12\)也需要一次双旋转
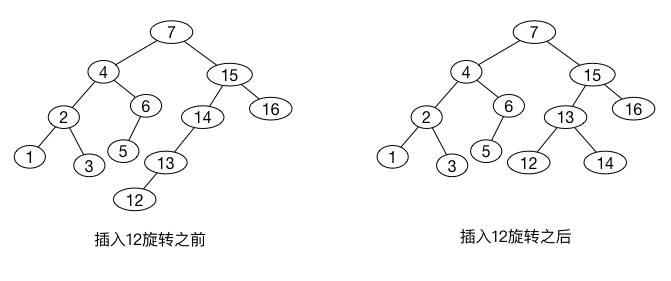
插入\(11\)、\(10\)都需要进行单旋转,接着我们插入\(8\)不需要进行旋转, 这样就建成了一颗近乎理想的平衡树
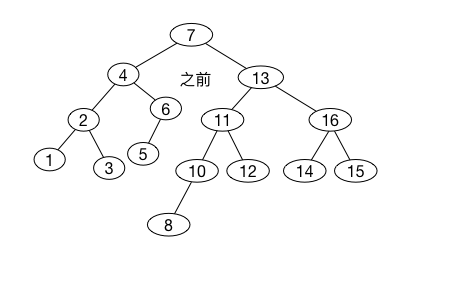
最后我们插入\(9\),在节点\(10\)发生不平衡,这里满足情形\(2\), 对左儿子的右子树进行一次,需要一次双旋转。
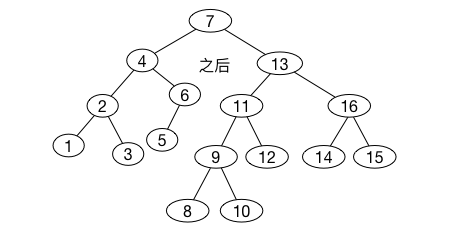
总结
现在让我们对上面的讨论做出总结,除几种情形外,编程的细节是相当简单的。 为将节点X插入AVL树T中,我们递归的将X插入到T的子树中。如果子树的高度不变, 那么插入完成;如果出现高度不平衡,那么找到不平衡点,做适当的单旋转或者双旋转, 更新这些高度,从而完成插入。
Scala实现
sealed trait AVLTree[+A] extends Serializable {
def balance: Int
def depth: Int
def contains[B >: A](x: B)(implicit ordering: Ordering[B]): Boolean
def insert[B >: A](x: B)(implicit ordering: Ordering[B]): AVLTree[B]
def rebalance[B >: A]: AVLTree[B]
}
/**
* 叶子节点
*/
case object Leaf extends AVLTree[Nothing] {
override val balance: Int = -1
override val depth: Int = 0
override def contains[B >: Nothing](x: B)(
implicit ordering: Ordering[B]): Boolean = false
override def insert[B >: Nothing](x: B)(
implicit ordering: Ordering[B]): AVLTree[B] = { Node(x, Leaf, Leaf) }
override def rebalance[B >: Nothing]: AVLTree[B] = this
}
case class Node[A](value: A, left: AVLTree[A], right: AVLTree[A]
) extends AVLTree[A]
{
override def balance: Int = right.depth - left.depth
override def depth: Int = math.max(left.depth, right.depth)
override def contains[B >: A](x: B)(
implicit ordering: Ordering[B]): Boolean = ???
override def insert[B >: A](x: B)(
implicit ordering: Ordering[B]): AVLTree[B] =
{
val cmp = ordering.compare(x,value)
if (cmp < 0){
Node(value, left.insert(x),right).rebalance
} else if (cmp > 0){
Node(value, left, right.insert(x)).rebalance
} else {
this
}
}
override def rebalance[B >: A] = {
if (-2 == balance){
if (1 == left.balance){
doubleRightRotation
} else {
rightRotation
}
} else if(2 == balance) {
if (-1 == right.balance){
doubleLeftRotation
}else {
leftRotation
}
} else {
this
}
}
/*
* 5
* \ 6
* 6 ---- 左单旋转 ---> / \
* \ 5 7
* 7
*
* 在节点5 发生不平衡 5的右节点成为新的根节点
*/
private def leftRotation[B >: A] = {
if (Leaf != right) {
val r = right.asInstanceOf[Node[A]]
Node(r.value, Node(value, left, r.left), r.right)
} else {
sys.error("should not happen.")
}
}
/*
* 7
* / 6
* 6 ---- 右单旋转 ---> / \
* / 5 7
* 5
*
* 在节点7 发生不平衡 7的左节点成为新的根节点
*/
private def rightRotation[B >: A] = {
if (Leaf != left) {
val l = left.asInstanceOf[Node[A]]
Node(l.value, l.left, Node(value, l.right, right))
} else {
sys.error("should not happen.")
}
}
/*
* 左双旋转
*
* 5 5
* \ \ 6
* 7 ----step1 ---> 6 ---step2---> / \
* / \ 5 7
* 6 7
*
* 在节点5处不平衡
* step1 : 节点5的右节点 做一次 右旋转
* step2 : 左旋转
*
*/
private def doubleLeftRotation[B >: A] = {
if (Leaf != right) {
val r = right.asInstanceOf[Node[A]]
val rightRotated = r.rightRotation
Node(rightRotated.value, Node(value, left, rightRotated.left),
rightRotated.right)
} else {
sys.error("should not happen.")
}
}
/*
* 右双旋转
*
* 7 7
* / / 6
* 5 ----step1 ---> 6 ---step2---> / \
* \ / 5 7
* 6 5
*
* 在节点7处不平衡
* step1 : 节点7的左节点 做一次 左旋转
* step2 : 右旋转
*
*/
private def doubleRightRotation[B >: A] = {
if (Leaf != left) {
val l: Node[A] = left.asInstanceOf[Node[A]]
val leftRotated = l.leftRotation
Node(leftRotated.value, leftRotated.left,
Node(value, leftRotated.right, right))
} else sys.error("Should not happen.")
}
}