字体栅格化的数学原理

贝赛尔曲线表示字体轮廓

贝赛尔曲线由一系列的点\(P_0 \cdots P_n\)组成，第一个点\(P_0\)与最后一点个\(P_N\)为起点与终点。 如果点的数量超过三个，那个中间的点都是控制曲线弯曲的「控制点」。

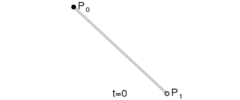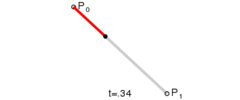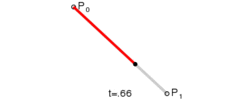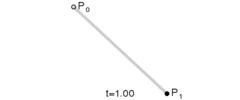
一次贝塞尔曲线用\(P_0\)和\(P_1\)表示，其实是一条直线

二次贝塞尔曲线\(P_0\)和\(P_2\)是起点和终点，\(P_1\)是控制点：

有了直线与曲线，则可以描述字体的轮廓了。

填充字体内部

判断点是否在轮廓内部

任意一点，向右作射线，计算射线与轮廓相交的次数：

• 0次表示在轮廓外。
• 大于0次：
  • 奇数次表示在轮廓内。
  • 双数次表示在轮廓外。

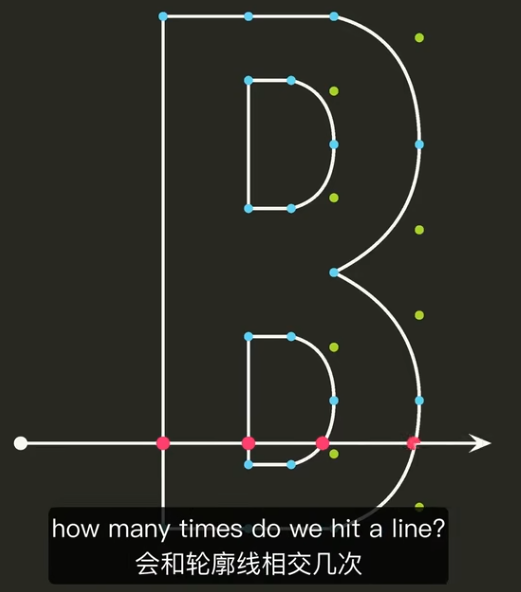
判断直线是否与贝赛尔曲线相交

如果要用函数\(P(t), t \in [0, 1]\) 来表示由\(P_0\)与\(P_1\)构成的贝塞尔曲线上的一点\(t\)， \(x=0\)时\(P(t) = P_0\)，\(x=1\)时\(P(t) = P_1\)，则有以下公式：

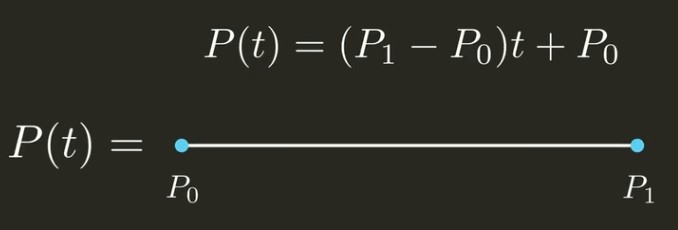
然后变化为：

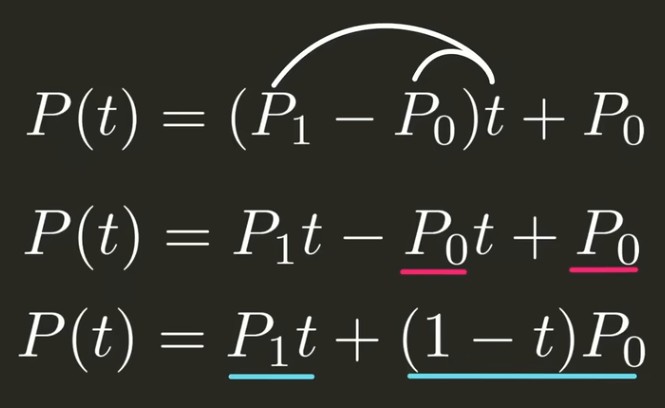
对于三个点的二次贝塞尔曲线，则可以把\(P_0, P_1\)和\(P_1, P_2\)代入之前的公式得到：

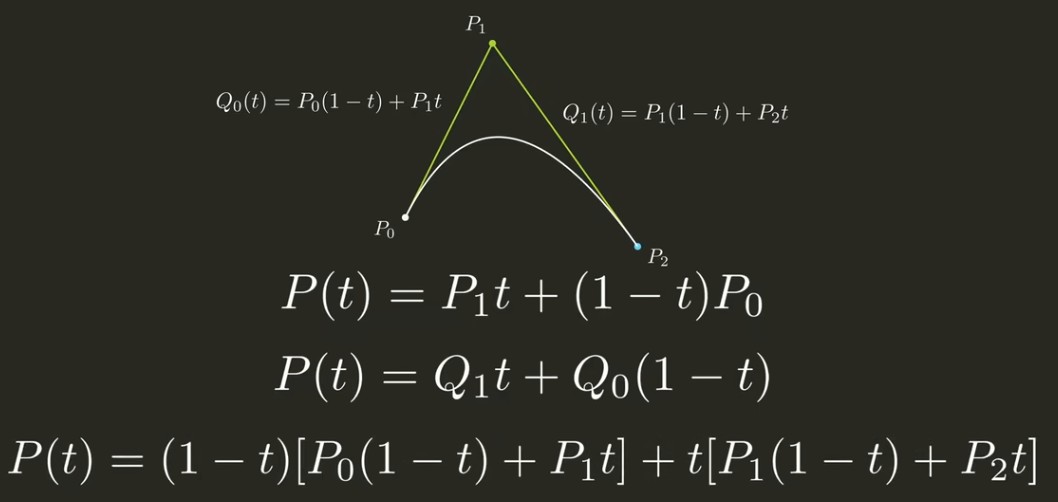
要判断一个点所在的水平射线是不是和贝寒尔曲线相交， 可以把这个点作为新坐标系的原点，判断曲线在新坐标系中是不是与X轴相交：

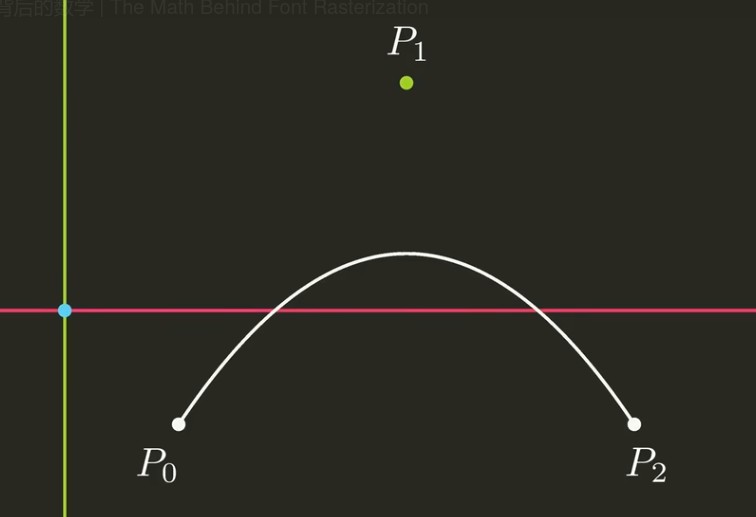
把之前的公式变形，变成一元二次方程的形式：

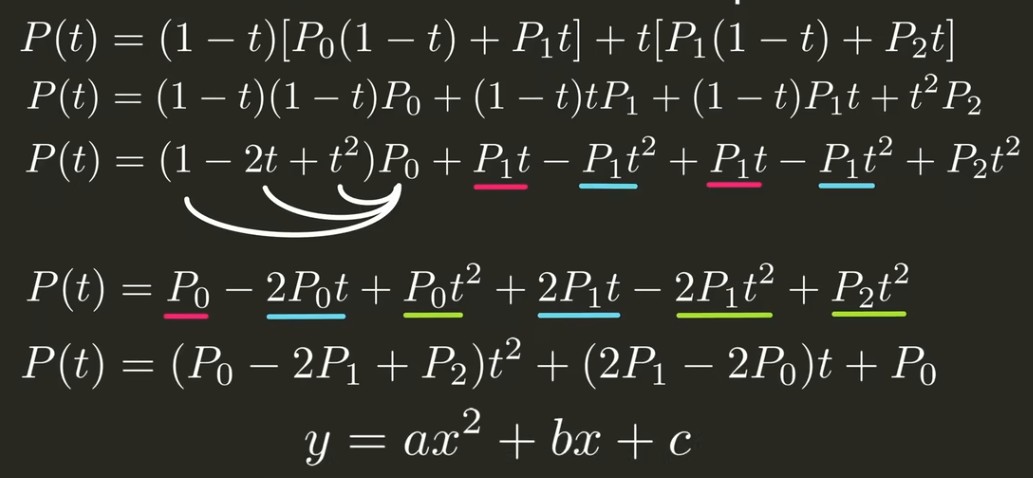
然后按一元二次方程是不是有解的方式来判断是不是与x轴相交：

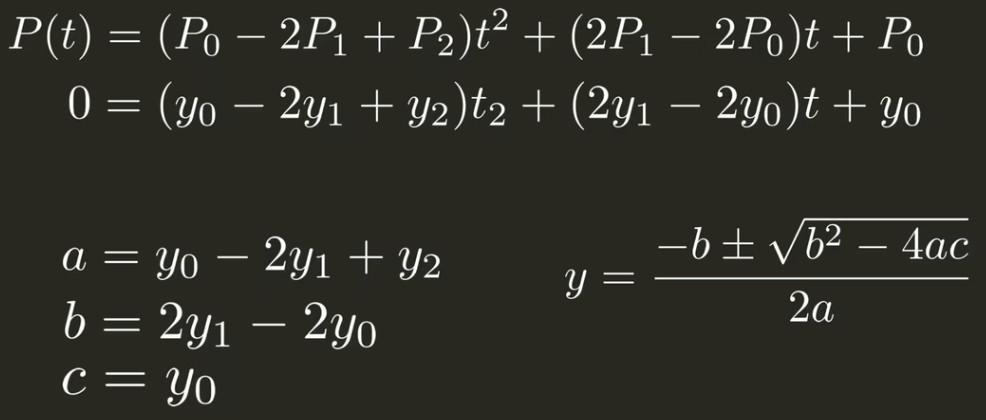
判别式：\(\Delta = b^2 -4ac\)

1. \(\Delta \gt 0\)，有两个不相等的实根
2. \(\Delta = 0\)，有两个相等的实根
3. \(\Delta \lt 0\)，无实根

\[ \begin{equation} \begin{split} \Delta &= (2y_1 - 2y_0)^2 - 4(y_0 - 2y_1 + y_2)y_0 \\ &= 4y_1^2 - 2 \times 2y_1 \times 2y_0 + 4y_0^2 - 4y_0(y_0 - 2y_1 + y_2) \\ &= 4y_1^2 - 8y_0 y_1 + 4y_0^2 - 4y_0^2 + 8y_0 y_1 - 4y_0 y_2 \\ &= 4y_1^2 - 4y_0 y_2 \end{split} \end{equation} \label{bzi_cross_pt} \]

更多边界状态

还有更多边界状态要处理，比如：

• 射线位于两个曲线的连接点上
• 射线与直线平行
• ……