gnuplot
系列教程:
http://blog.sciencenet.cn/blog-373392-518247.html
基本环境
命令gnuplot启动repl交互:
$ gnuplot
G N U P L O T
Version 4.6 patchlevel 4 last modified 2013-10-02
Build System: Linux x86_64
Copyright (C) 1986-1993, 1998, 2004, 2007-2013
Thomas Williams, Colin Kelley and many others
gnuplot home: http://www.gnuplot.info
faq, bugs, etc: type "help FAQ"
immediate help: type "help" (plot window: hit 'h')
Terminal type set to 'wxt'
gnuplot>
执行再有的脚本:
gnuplot> load 'plot.plt'
调用系统命令:
!vim plot.plt
绘制二维图像
plot指令可以用来绘制二维图像:
plot sin(x) linewidth 4
-
help plot查看帮助信息。 -
linewidth指定函数线条的粗细。 -
笛卡尔坐标系下默认的变量名为
x,默认的范围在\(-10 ~ 10\)。 -
如果变量名不用
x的话会报错,如plot sin(y)就报错「undefined varible: y」
保存图像
set term png # 定义图像格式 set output "sin.png" # 保存的文件名 plot sin(x)
查看所有支持的格式:
gnuplot> set term
Available terminal types:
cairolatex LaTeX picture environment using graphicx package and Cairo backend
canvas HTML Canvas object
cgm Computer Graphics Metafile
context ConTeXt with MetaFun (for PDF documents)
corel EPS format for CorelDRAW
dumb ascii art for anything that prints text
dxf dxf-file for AutoCad (default size 120x80)
eepic EEPIC -- extended LaTeX picture environment
emf Enhanced Metafile format
emtex LaTeX picture environment with emTeX specials
epscairo eps terminal based on cairo
epslatex LaTeX picture environment using graphicx package
fig FIG graphics language for XFIG graphics editor
gif GIF images using libgd and TrueType fonts
gpic GPIC -- Produce graphs in groff using the gpic preprocessor
hp2623A HP2623A and maybe others
hp2648 HP2648 and HP2647
hpgl HP7475 and relatives [number of pens] [eject]
imagen Imagen laser printer
jpeg JPEG images using libgd and TrueType fonts
latex LaTeX picture environment
Press return for more:
一般LaTeX中使用eps或是epslatex比较常见:
set term postscript set output "sin.eps"
Gnuplot基本程序结构
# Bipolar Transistor (NPN) Mutual Characteristic # comment Ie(Vbe) = Ies*exp(Vbe/kT_q) # defined functions Ic(Vbe) = alpha*Ie(Vbe)+Ico # and constants alpha = 0.99 Ies = 4e-14 Ico = 1e-09 kT_q = 0.025 set dummy Vbe # set plotting environment set grid set samples 160 set title "Mutual Characteristic of a Transistor" set xlabel "Vbe (base emmitter voltage)" set xrange [0 : 0.75] set ylabel "Ic (collector current)" set yrange [0 : 0.005] # set key 0.2,0.0045 set format y "%.4f" plot Ic(Vbe) # plotting set terminal postscript # output set output "npn.ps" replot
图像设置
设置图像大小
set term png size 600,400
字体设置
set term png size 600,400 enhanced font "Sans"
选项enhanced可以用来显示特殊符号,比如「\(\pi\)」
标题设置
set title 'sketch of sine function'
边框设置
unset border # 不显示外框
显示图例
set key off
配置坐标轴
设置范围
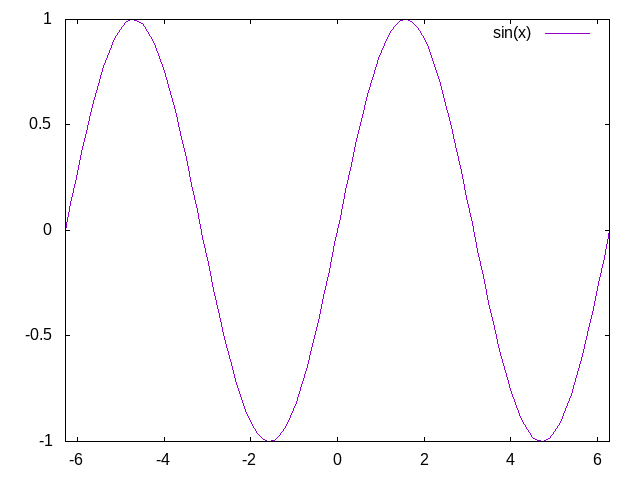
设置\(x\)轴\(y\)轴的范围:
set xrange [-2*pi : 2*pi] set yrange [-1 : 1] plot sin(x) title "sin(x)"
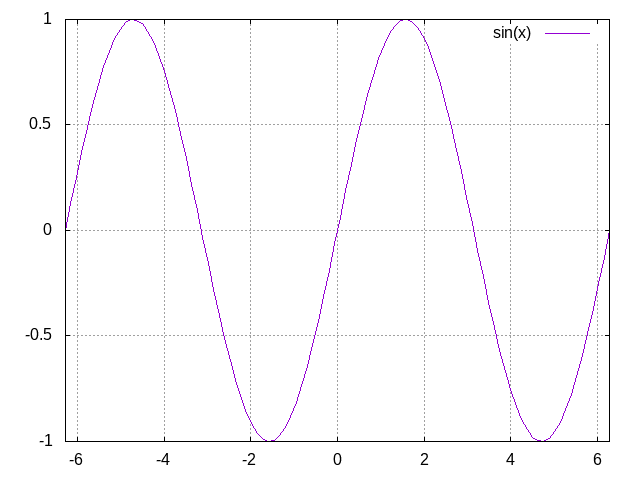
设置网络
set grid xtics set grid ytics
设置标签
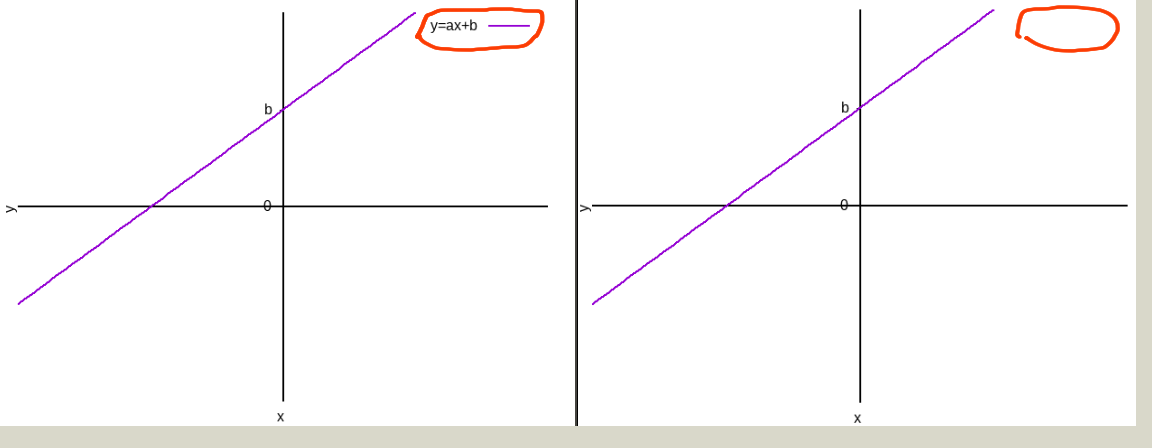
设置\(x\)轴与\(y\)轴的标注:
set xlabel "x" set ylabel "y"
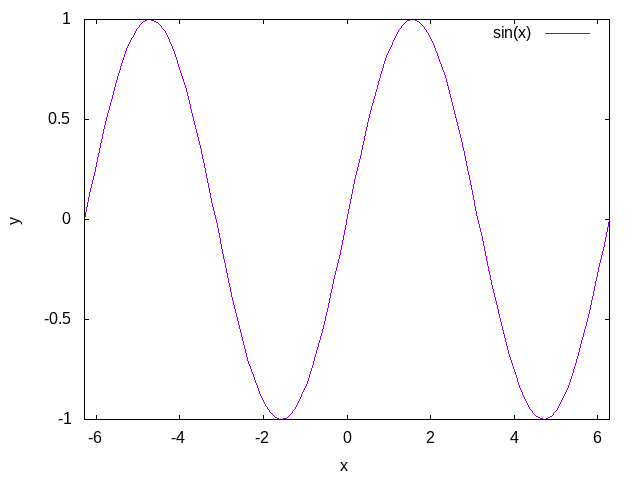
设置刻度
默认刻度
默认刻度会平均刻度的间距。
不显示刻度
unset xtics unset ytics
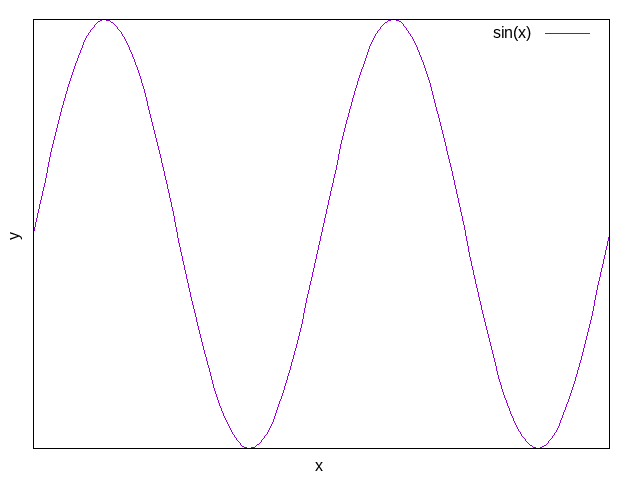
指定刻度
格式一:每一个刻度的值和标题
set xtics ('-2{/Symbol p}' -2 * pi, '-{/Symbol p}' -pi, '0' 0, '{/Symbol p}' pi, '2{/Symbol p}' 2 * pi)
格式二:最小,步长,最大
set ytics -1, 0.5, 1
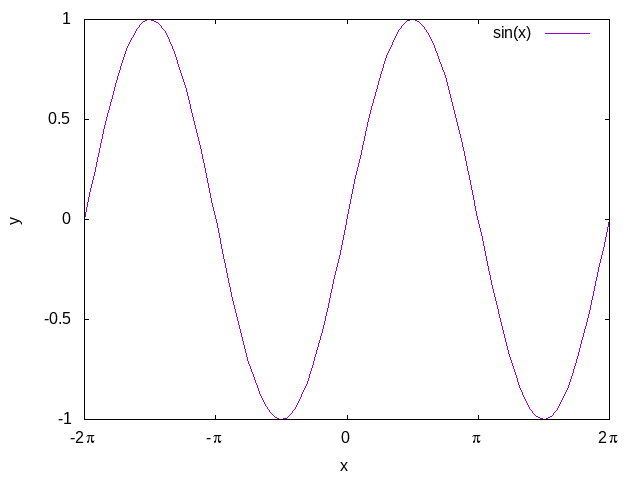
不显示外框
unset border # 不显示外框
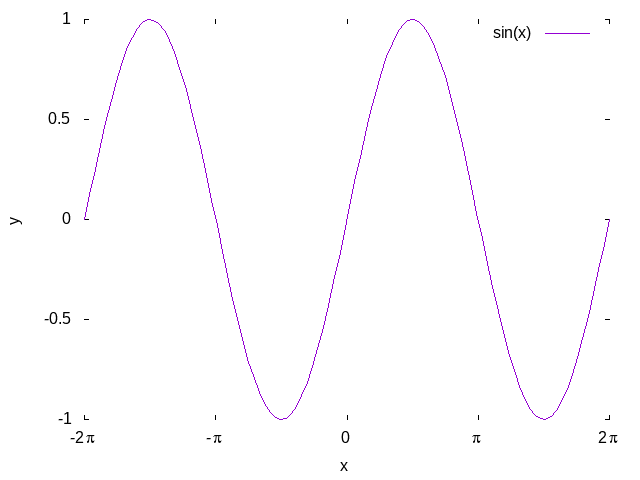
显示X轴与Y轴
set zeroaxis lt -1 lw 2 # 画出X轴与Y轴
set xtics axis ('-2{/Symbol p}' -2 * pi, '-{/Symbol p}' -pi, '0' 0, '{/Symbol p}' pi, '2{/Symbol p}' 2 * pi)
set ytics axis -1, 0.5, 1
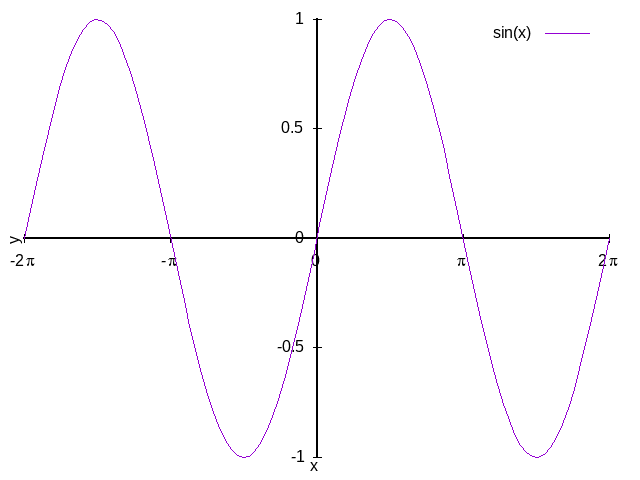
绘制函数
支持的函数
__________________________________________________________ Function Returns ----------- ------------------------------------------ abs(x) absolute value of x, |x| acos(x) arc-cosine of x asin(x) arc-sine of x atan(x) arc-tangent of x cos(x) cosine of x, x is in radians. cosh(x) hyperbolic cosine of x, x is in radians erf(x) error function of x exp(x) exponential function of x, base e inverf(x) inverse error function of x invnorm(x) inverse normal distribution of x log(x) log of x, base e log10(x) log of x, base 10 norm(x) normal Gaussian distribution function rand(x) pseudo-random number generator sgn(x) 1 if x > 0, -1 if x < 0, 0 if x=0 sin(x) sine of x, x is in radians sinh(x) hyperbolic sine of x, x is in radians sqrt(x) the square root of x tan(x) tangent of x, x is in radians tanh(x) hyperbolic tangent of x, x is in radians ___________________________________________________________ Bessel, gamma, ibeta, igamma, and lgamma functions are also supported. Many functions can take complex arguments. Binary and unary operators are also supported.
绘制多个函数
plot x**2 title "f(x)" , \
3*x - 2 title "(f(x+{/symbol D}x)-f(x))/{/symbol D}x" , \
2*x - 1 title "f'(x)"
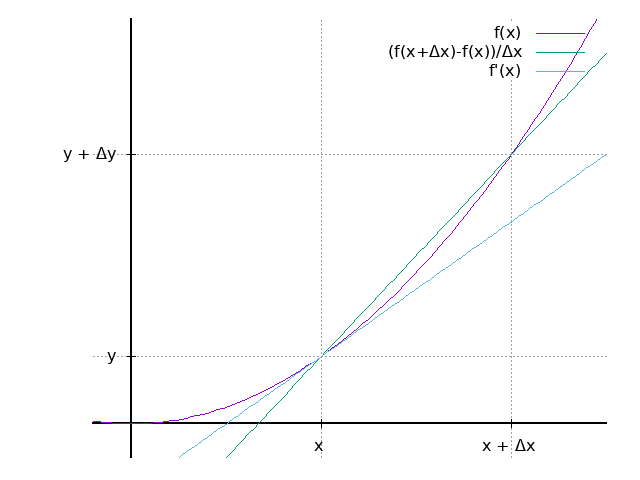
定义常量
e=2.7182818284
mu = 0
sgm = 1
x0 = mu - 3*sgm
x1 = mu - 2*sgm
x2 = mu - sgm
x3 = mu
x4 = mu + sgm
x5 = mu + 2*sgm
x6 = mu + 3*sgm
# 坐标轴上的刻度 σ μ
set xtics axis ( \
"μ{/symbol m}-3{/symbol s}" x0, \
"{/symbol m}-2{/symbol s}" x1, \
"{/symbol m}-{/symbol s}" x2, \
"{/symbol m}"x3, \
"{/symbol m}+{/symbol s}" x4, \
"{/symbol m}+2{/symbol s}" x5, \
"{/symbol m}+3{/symbol s}" x6)
set ytics axis
plot 1/(sqrt(2 * pi) * sgm) * e ** (-1 * (x - mu)**2 / (2 * sgm**2)) \
title "sigmoid(x)"
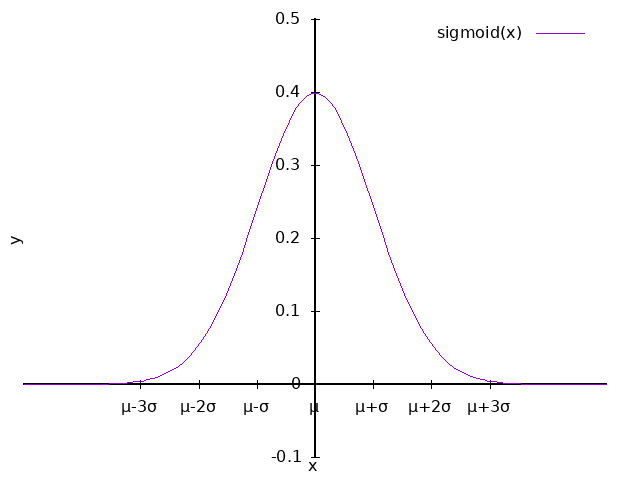
定义函数
f(x)= x>2.2 && x<10 ? \
(x-3) ** 3 + 25 : \
3*x**4 - 4*x**3 - 12*x**2 + 35
plot f(x)
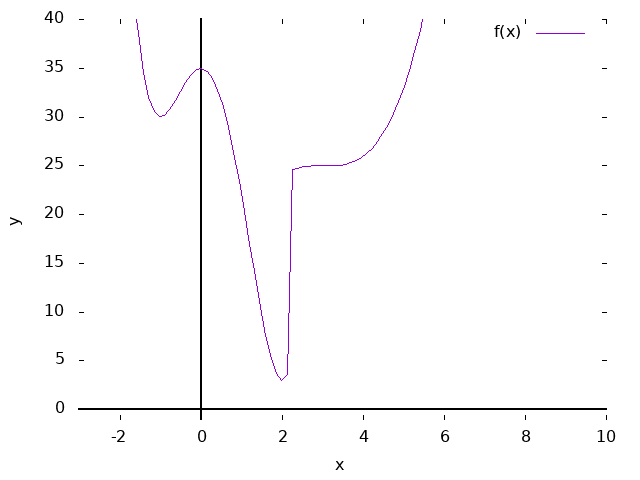
从数据文件绘制图形
数据文件data.dat:
0.1 1.9209304925688333 0.2 1.556593079864876 0.30000000000000004 1.1884832854699365 0.4 0.8430151183100703 0.5 0.5403023058681398 0.6000000000000001 0.2935097811261054 0.7000000000000001 0.1087789714561541 0.8 -0.014307765927631517 0.9 -0.08179275408951135 1.0 -0.1040367091367856 1.1 -0.09416017876085528 1.2000000000000002 -0.06636543439871205 1.3 -0.03427555013475787 1.4000000000000001 -0.009422223406686558 1.5 -0.0 1.6 -0.00998294775794755 1.7000000000000002 -0.0386719277031785 1.8 -0.08070825747007325 1.9000000000000001 -0.12655483390630673 2.0 -0.16341090521590299 2.1 -0.17649389568265184 2.2 -0.15059310628942557 2.3000000000000003 -0.07177761723843461 2.4000000000000004 0.07087417658595234 2.5 0.28366218546322625 2.6 0.5669051722734564 2.7 0.9139577413573942 2.8000000000000003 1.3107063346823233 2.9000000000000004 1.7356182532049869 3.0 2.1603831449633235
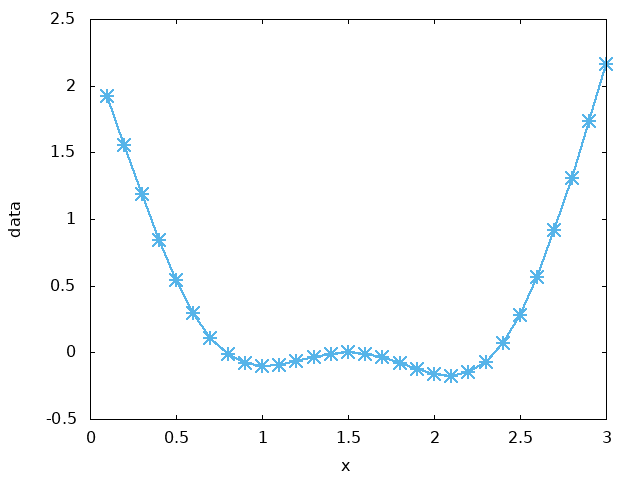
使用linespoints画图,线宽2.5、线的类型为3:
set xlabel "x" set ylabel "data" set pointsize 2.0 plot 'data.dat' with linespoints linewidth 2.5 linetype 3 notitle
绘标注
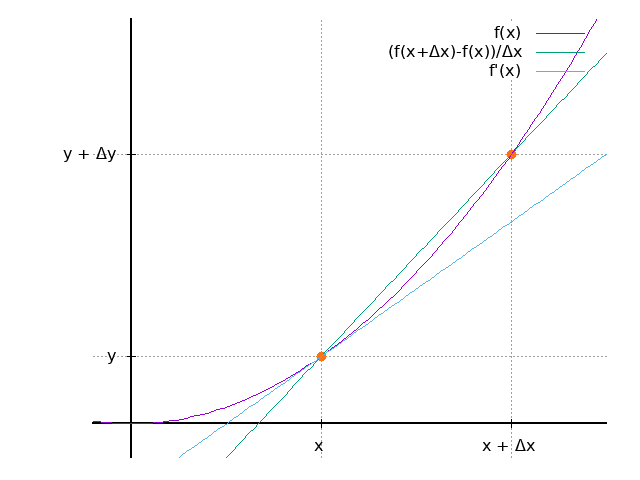
标注点
set label 1 at 1,1 point pt 7 ps 1.5 lc rgb "#F87217" set label 3 at 2,4 point pt 7 ps 1.5 lc rgb "#F87217"
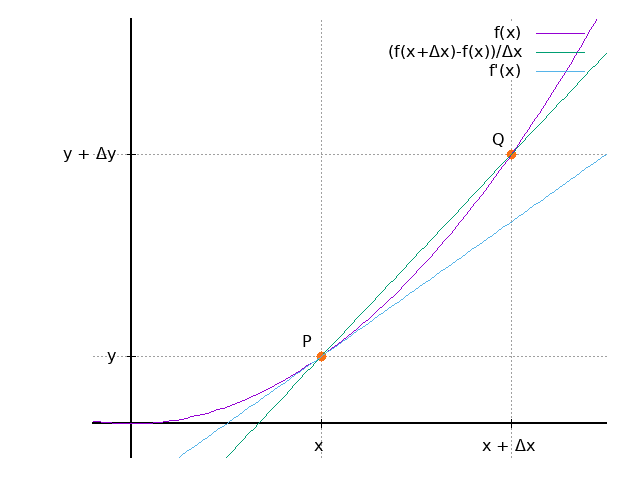
文字描述
set label 2 "P" at 0.9,1.2 set label 4 "Q" at 1.9,4.2
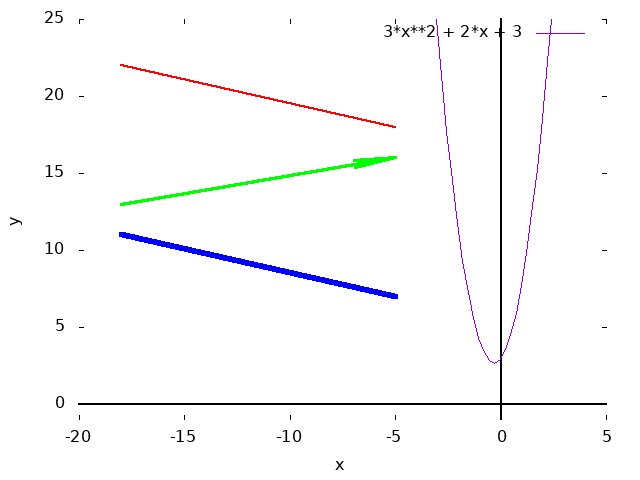
箭头与线段
set arrow 1 from -18,22 to -5,18 nofilled size 0.1,0.1,0.1 lc rgb "#ff0000" lw 2 set arrow 2 from -18,13 to -5,16 nofilled size 2.0,5.0,5.0 lc rgb "#00ff00" lw 3 set arrow 3 from -18,11 to -5,7 nofilled size 0.1,0.1,0.1 lc rgb "#0000ff" lw 5
绘制三维图像
splot命令用来绘制三维图像,两个变量分别是x和y:
set xrange [-2 * pi : 2 * pi] set yrange [-2 * pi : 2 * pi] splot sin(x) * sin(y)
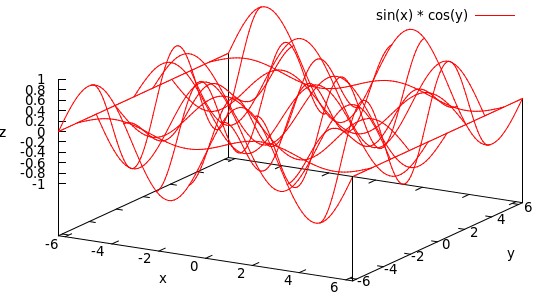
定义等值线的密度
set isosamples 75, 75 replot
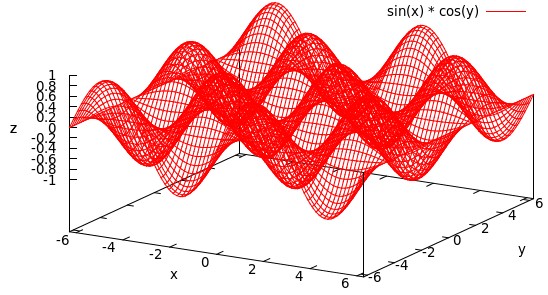
隐藏三维图像的背面线条
隐藏背面的线条:
set hidden3d replot
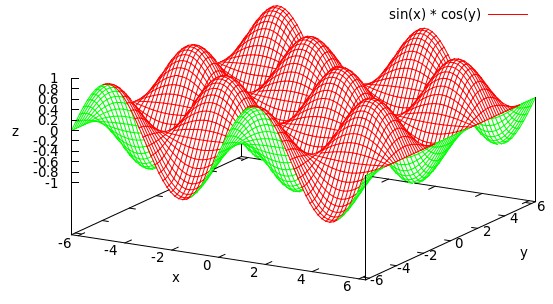
调整Z轴
把z轴的零点移到xy平面上:
set ticslevel 0 replot
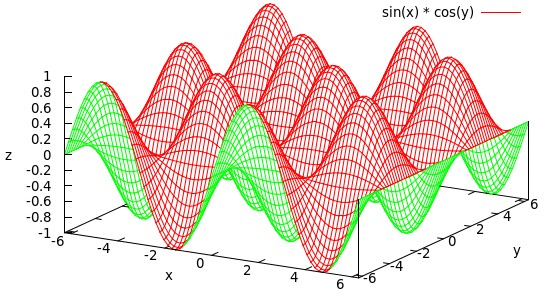
调整观察角度
gnuplot窗口中显示的3维图像可以用鼠标调整角度。
如果输出是文件,可以用set view定义角度,四个参数的意义请查看手册。
set view *, *, *, *
等高线
因为没有专门的等高线命令,所以还是使用splot二维绘制实现:
set xrange [-2 * pi : 2 * pi] set yrange [-2 * pi : 2 * pi] set isosamples 100,100 set hidden3d set contour base # 在底部显示等高线 splot sin(x) * cos(y) notitle
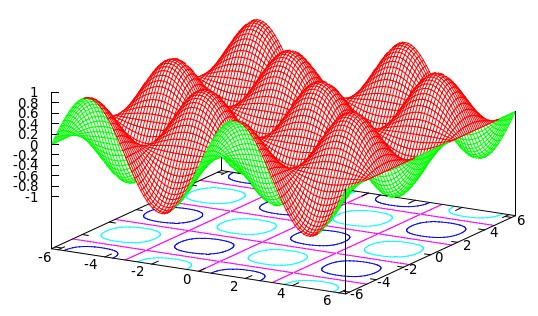
调整只显示等高线:
unset surface # 不显示三维部分,只显示等高线 set view map # 以map角度观察图像 set key out # 在图像杠外显示图例 replot
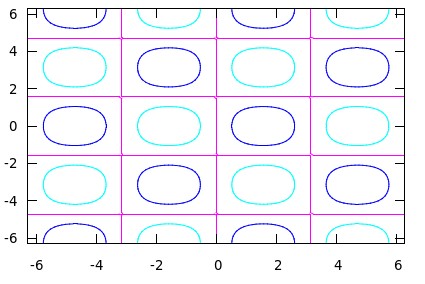
把等高线的设置得更加密致:
set cntrparam levels discrete -0.8, -0.6, -0.4, -0.2, 0, 0.2, 0.4, 0.6, 0.8 set xlabel 'x' set ylabel 'y' set title 'z=sin(x)*cos(y)` replot
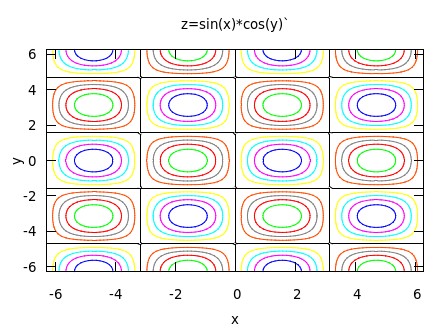
从数据文件绘制三维视图
0.1 0.1 0.01999999999999999 0.1 0.2 0.02999999999999997 0.1 0.30000000000000004 -0.020000000000000018 0.1 0.4 -0.13000000000000006 0.1 0.5 -0.3 0.1 0.6000000000000001 -0.5300000000000002 0.1 0.7000000000000001 -0.8200000000000002 0.1 0.8 -1.1700000000000004 0.1 0.9 -1.58 0.1 1.0 -2.05 0.1 1.1 -2.580000000000001 0.1 1.2000000000000002 -3.170000000000001 0.1 1.3 -3.8200000000000003 0.1 1.4000000000000001 -4.530000000000001 0.1 1.5 -5.3 0.1 1.6 -6.130000000000002 0.1 1.7000000000000002 -7.020000000000001 0.1 1.8 -7.970000000000001 0.1 1.9000000000000001 -8.980000000000002 0.1 2.0 -10.05 0.1 2.1 -11.18 0.2 0.1 -0.13000000000000003 0.2 0.2 -0.12000000000000005 0.2 0.30000000000000004 -0.17000000000000007 0.2 0.4 -0.28000000000000014 0.2 0.5 -0.45000000000000007 0.2 0.6000000000000001 -0.6800000000000003 0.2 0.7000000000000001 -0.9700000000000002 0.2 0.8 -1.3200000000000003 0.2 0.9 -1.7300000000000002 0.2 1.0 -2.2 0.2 1.1 -2.730000000000001 0.2 1.2000000000000002 -3.320000000000001 0.2 1.3 -3.97 0.2 1.4000000000000001 -4.680000000000001 0.2 1.5 -5.45 0.2 1.6 -6.280000000000001 0.2 1.7000000000000002 -7.170000000000002 0.2 1.8 -8.120000000000001 0.2 1.9000000000000001 -9.130000000000003 0.2 2.0 -10.2 0.2 2.1 -11.33 0.30000000000000004 0.1 -0.3800000000000001 0.30000000000000004 0.2 -0.3700000000000001 0.30000000000000004 0.30000000000000004 -0.42000000000000015 0.30000000000000004 0.4 -0.5300000000000002 0.30000000000000004 0.5 -0.7000000000000002 0.30000000000000004 0.6000000000000001 -0.9300000000000004 0.30000000000000004 0.7000000000000001 -1.2200000000000002 0.30000000000000004 0.8 -1.5700000000000005 0.30000000000000004 0.9 -1.9800000000000002 0.30000000000000004 1.0 -2.45 0.30000000000000004 1.1 -2.980000000000001 0.30000000000000004 1.2000000000000002 -3.570000000000001 0.30000000000000004 1.3 -4.220000000000001 0.30000000000000004 1.4000000000000001 -4.930000000000001 0.30000000000000004 1.5 -5.7 0.30000000000000004 1.6 -6.530000000000001 0.30000000000000004 1.7000000000000002 -7.420000000000002 0.30000000000000004 1.8 -8.370000000000001 0.30000000000000004 1.9000000000000001 -9.380000000000003 0.30000000000000004 2.0 -10.45 0.30000000000000004 2.1 -11.58 0.4 0.1 -0.7300000000000002 0.4 0.2 -0.7200000000000001 0.4 0.30000000000000004 -0.7700000000000002 0.4 0.4 -0.8800000000000002 0.4 0.5 -1.0500000000000003 0.4 0.6000000000000001 -1.2800000000000002 0.4 0.7000000000000001 -1.5700000000000003 0.4 0.8 -1.9200000000000004 0.4 0.9 -2.33 0.4 1.0 -2.8000000000000003 0.4 1.1 -3.330000000000001 0.4 1.2000000000000002 -3.9200000000000013 0.4 1.3 -4.57 0.4 1.4000000000000001 -5.280000000000001 0.4 1.5 -6.05 0.4 1.6 -6.880000000000002 0.4 1.7000000000000002 -7.770000000000001 0.4 1.8 -8.72 0.4 1.9000000000000001 -9.730000000000002 0.4 2.0 -10.8 0.4 2.1 -11.93 0.5 0.1 -1.18 0.5 0.2 -1.1700000000000002 0.5 0.30000000000000004 -1.22 0.5 0.4 -1.33 0.5 0.5 -1.5 0.5 0.6000000000000001 -1.7300000000000002 0.5 0.7000000000000001 -2.02 0.5 0.8 -2.37 0.5 0.9 -2.7800000000000002 0.5 1.0 -3.25 0.5 1.1 -3.7800000000000007 0.5 1.2000000000000002 -4.370000000000001 0.5 1.3 -5.0200000000000005 0.5 1.4000000000000001 -5.73 0.5 1.5 -6.5 0.5 1.6 -7.330000000000002 0.5 1.7000000000000002 -8.220000000000002 0.5 1.8 -9.17 0.5 1.9000000000000001 -10.180000000000001 0.5 2.0 -11.25 0.5 2.1 -12.38 0.6000000000000001 0.1 -1.7300000000000004 0.6000000000000001 0.2 -1.7200000000000006 0.6000000000000001 0.30000000000000004 -1.7700000000000005 0.6000000000000001 0.4 -1.8800000000000003 0.6000000000000001 0.5 -2.0500000000000007 0.6000000000000001 0.6000000000000001 -2.2800000000000007 0.6000000000000001 0.7000000000000001 -2.5700000000000007 0.6000000000000001 0.8 -2.920000000000001 0.6000000000000001 0.9 -3.3300000000000005 0.6000000000000001 1.0 -3.8000000000000007 0.6000000000000001 1.1 -4.330000000000001 0.6000000000000001 1.2000000000000002 -4.920000000000002 0.6000000000000001 1.3 -5.57 0.6000000000000001 1.4000000000000001 -6.280000000000001 0.6000000000000001 1.5 -7.050000000000001 0.6000000000000001 1.6 -7.880000000000002 0.6000000000000001 1.7000000000000002 -8.770000000000001 0.6000000000000001 1.8 -9.72 0.6000000000000001 1.9000000000000001 -10.730000000000002 0.6000000000000001 2.0 -11.8 0.6000000000000001 2.1 -12.930000000000001 0.7000000000000001 0.1 -2.3800000000000003 0.7000000000000001 0.2 -2.3700000000000006 0.7000000000000001 0.30000000000000004 -2.4200000000000004 0.7000000000000001 0.4 -2.5300000000000007 0.7000000000000001 0.5 -2.7000000000000006 0.7000000000000001 0.6000000000000001 -2.9300000000000006 0.7000000000000001 0.7000000000000001 -3.2200000000000006 0.7000000000000001 0.8 -3.570000000000001 0.7000000000000001 0.9 -3.980000000000001 0.7000000000000001 1.0 -4.450000000000001 0.7000000000000001 1.1 -4.980000000000001 0.7000000000000001 1.2000000000000002 -5.570000000000002 0.7000000000000001 1.3 -6.220000000000001 0.7000000000000001 1.4000000000000001 -6.9300000000000015 0.7000000000000001 1.5 -7.700000000000001 0.7000000000000001 1.6 -8.530000000000001 0.7000000000000001 1.7000000000000002 -9.420000000000002 0.7000000000000001 1.8 -10.370000000000001 0.7000000000000001 1.9000000000000001 -11.380000000000003 0.7000000000000001 2.0 -12.450000000000001 0.7000000000000001 2.1 -13.580000000000002 0.8 0.1 -3.1300000000000003 0.8 0.2 -3.1200000000000006 0.8 0.30000000000000004 -3.1700000000000004 0.8 0.4 -3.2800000000000007 0.8 0.5 -3.4500000000000006 0.8 0.6000000000000001 -3.6800000000000006 0.8 0.7000000000000001 -3.9700000000000006 0.8 0.8 -4.32 0.8 0.9 -4.73 0.8 1.0 -5.200000000000001 0.8 1.1 -5.730000000000001 0.8 1.2000000000000002 -6.320000000000002 0.8 1.3 -6.970000000000001 0.8 1.4000000000000001 -7.6800000000000015 0.8 1.5 -8.450000000000001 0.8 1.6 -9.280000000000001 0.8 1.7000000000000002 -10.170000000000002 0.8 1.8 -11.120000000000001 0.8 1.9000000000000001 -12.130000000000003 0.8 2.0 -13.200000000000001 0.8 2.1 -14.330000000000002 0.9 0.1 -3.9800000000000004 0.9 0.2 -3.9700000000000006 0.9 0.30000000000000004 -4.020000000000001 0.9 0.4 -4.130000000000001 0.9 0.5 -4.300000000000001 0.9 0.6000000000000001 -4.530000000000001 0.9 0.7000000000000001 -4.82 0.9 0.8 -5.170000000000002 0.9 0.9 -5.580000000000001 0.9 1.0 -6.050000000000001 0.9 1.1 -6.580000000000002 0.9 1.2000000000000002 -7.170000000000002 0.9 1.3 -7.820000000000001 0.9 1.4000000000000001 -8.530000000000001 0.9 1.5 -9.3 0.9 1.6 -10.130000000000003 0.9 1.7000000000000002 -11.020000000000003 0.9 1.8 -11.970000000000002 0.9 1.9000000000000001 -12.980000000000002 0.9 2.0 -14.05 0.9 2.1 -15.180000000000001 1.0 0.1 -4.930000000000001 1.0 0.2 -4.92 1.0 0.30000000000000004 -4.970000000000001 1.0 0.4 -5.08 1.0 0.5 -5.25 1.0 0.6000000000000001 -5.48 1.0 0.7000000000000001 -5.77 1.0 0.8 -6.120000000000001 1.0 0.9 -6.529999999999999 1.0 1.0 -7.0 1.0 1.1 -7.530000000000001 1.0 1.2000000000000002 -8.120000000000001 1.0 1.3 -8.77 1.0 1.4000000000000001 -9.48 1.0 1.5 -10.25 1.0 1.6 -11.080000000000002 1.0 1.7000000000000002 -11.970000000000002 1.0 1.8 -12.920000000000002 1.0 1.9000000000000001 -13.930000000000001 1.0 2.0 -15.0 1.0 2.1 -16.13 1.1 0.1 -5.980000000000001 1.1 0.2 -5.970000000000001 1.1 0.30000000000000004 -6.020000000000001 1.1 0.4 -6.130000000000001 1.1 0.5 -6.300000000000001 1.1 0.6000000000000001 -6.530000000000001 1.1 0.7000000000000001 -6.82 1.1 0.8 -7.170000000000002 1.1 0.9 -7.58 1.1 1.0 -8.05 1.1 1.1 -8.580000000000002 1.1 1.2000000000000002 -9.170000000000002 1.1 1.3 -9.82 1.1 1.4000000000000001 -10.530000000000001 1.1 1.5 -11.3 1.1 1.6 -12.130000000000003 1.1 1.7000000000000002 -13.020000000000003 1.1 1.8 -13.970000000000002 1.1 1.9000000000000001 -14.980000000000002 1.1 2.0 -16.05 1.1 2.1 -17.18 1.2000000000000002 0.1 -7.130000000000003 1.2000000000000002 0.2 -7.120000000000002 1.2000000000000002 0.30000000000000004 -7.170000000000003 1.2000000000000002 0.4 -7.280000000000002 1.2000000000000002 0.5 -7.450000000000002 1.2000000000000002 0.6000000000000001 -7.6800000000000015 1.2000000000000002 0.7000000000000001 -7.970000000000002 1.2000000000000002 0.8 -8.320000000000002 1.2000000000000002 0.9 -8.730000000000002 1.2000000000000002 1.0 -9.200000000000003 1.2000000000000002 1.1 -9.730000000000002 1.2000000000000002 1.2000000000000002 -10.320000000000004 1.2000000000000002 1.3 -10.970000000000002 1.2000000000000002 1.4000000000000001 -11.680000000000003 1.2000000000000002 1.5 -12.450000000000003 1.2000000000000002 1.6 -13.280000000000003 1.2000000000000002 1.7000000000000002 -14.170000000000003 1.2000000000000002 1.8 -15.120000000000003 1.2000000000000002 1.9000000000000001 -16.130000000000003 1.2000000000000002 2.0 -17.200000000000003 1.2000000000000002 2.1 -18.330000000000002 1.3 0.1 -8.38 1.3 0.2 -8.370000000000001 1.3 0.30000000000000004 -8.42 1.3 0.4 -8.530000000000001 1.3 0.5 -8.700000000000001 1.3 0.6000000000000001 -8.930000000000001 1.3 0.7000000000000001 -9.22 1.3 0.8 -9.570000000000002 1.3 0.9 -9.98 1.3 1.0 -10.450000000000001 1.3 1.1 -10.980000000000002 1.3 1.2000000000000002 -11.570000000000002 1.3 1.3 -12.220000000000002 1.3 1.4000000000000001 -12.930000000000001 1.3 1.5 -13.700000000000001 1.3 1.6 -14.530000000000003 1.3 1.7000000000000002 -15.420000000000002 1.3 1.8 -16.37 1.3 1.9000000000000001 -17.380000000000003 1.3 2.0 -18.450000000000003 1.3 2.1 -19.580000000000002 1.4000000000000001 0.1 -9.730000000000002 1.4000000000000001 0.2 -9.720000000000002 1.4000000000000001 0.30000000000000004 -9.770000000000001 1.4000000000000001 0.4 -9.880000000000003 1.4000000000000001 0.5 -10.050000000000002 1.4000000000000001 0.6000000000000001 -10.280000000000003 1.4000000000000001 0.7000000000000001 -10.570000000000004 1.4000000000000001 0.8 -10.920000000000002 1.4000000000000001 0.9 -11.330000000000002 1.4000000000000001 1.0 -11.800000000000002 1.4000000000000001 1.1 -12.330000000000004 1.4000000000000001 1.2000000000000002 -12.920000000000002 1.4000000000000001 1.3 -13.570000000000002 1.4000000000000001 1.4000000000000001 -14.280000000000003 1.4000000000000001 1.5 -15.050000000000002 1.4000000000000001 1.6 -15.880000000000004 1.4000000000000001 1.7000000000000002 -16.770000000000003 1.4000000000000001 1.8 -17.720000000000002 1.4000000000000001 1.9000000000000001 -18.730000000000004 1.4000000000000001 2.0 -19.800000000000004 1.4000000000000001 2.1 -20.930000000000003 1.5 0.1 -11.18 1.5 0.2 -11.17 1.5 0.30000000000000004 -11.219999999999999 1.5 0.4 -11.33 1.5 0.5 -11.5 1.5 0.6000000000000001 -11.73 1.5 0.7000000000000001 -12.020000000000001 1.5 0.8 -12.37 1.5 0.9 -12.78 1.5 1.0 -13.25 1.5 1.1 -13.780000000000001 1.5 1.2000000000000002 -14.370000000000001 1.5 1.3 -15.02 1.5 1.4000000000000001 -15.73 1.5 1.5 -16.5 1.5 1.6 -17.330000000000002 1.5 1.7000000000000002 -18.220000000000002 1.5 1.8 -19.17 1.5 1.9000000000000001 -20.18 1.5 2.0 -21.25 1.5 2.1 -22.380000000000003 1.6 0.1 -12.730000000000002 1.6 0.2 -12.720000000000002 1.6 0.30000000000000004 -12.770000000000001 1.6 0.4 -12.880000000000003 1.6 0.5 -13.050000000000002 1.6 0.6000000000000001 -13.280000000000003 1.6 0.7000000000000001 -13.570000000000004 1.6 0.8 -13.920000000000002 1.6 0.9 -14.330000000000002 1.6 1.0 -14.800000000000002 1.6 1.1 -15.330000000000004 1.6 1.2000000000000002 -15.920000000000002 1.6 1.3 -16.57 1.6 1.4000000000000001 -17.28 1.6 1.5 -18.050000000000004 1.6 1.6 -18.880000000000003 1.6 1.7000000000000002 -19.770000000000003 1.6 1.8 -20.720000000000002 1.6 1.9000000000000001 -21.730000000000004 1.6 2.0 -22.800000000000004 1.6 2.1 -23.930000000000003 1.7000000000000002 0.1 -14.380000000000003 1.7000000000000002 0.2 -14.370000000000003 1.7000000000000002 0.30000000000000004 -14.420000000000002 1.7000000000000002 0.4 -14.530000000000003 1.7000000000000002 0.5 -14.700000000000003 1.7000000000000002 0.6000000000000001 -14.930000000000003 1.7000000000000002 0.7000000000000001 -15.220000000000004 1.7000000000000002 0.8 -15.570000000000002 1.7000000000000002 0.9 -15.980000000000002 1.7000000000000002 1.0 -16.450000000000003 1.7000000000000002 1.1 -16.980000000000004 1.7000000000000002 1.2000000000000002 -17.570000000000004 1.7000000000000002 1.3 -18.220000000000002 1.7000000000000002 1.4000000000000001 -18.930000000000003 1.7000000000000002 1.5 -19.700000000000003 1.7000000000000002 1.6 -20.530000000000005 1.7000000000000002 1.7000000000000002 -21.420000000000005 1.7000000000000002 1.8 -22.370000000000005 1.7000000000000002 1.9000000000000001 -23.380000000000003 1.7000000000000002 2.0 -24.450000000000003 1.7000000000000002 2.1 -25.580000000000005 1.8 0.1 -16.130000000000003 1.8 0.2 -16.120000000000005 1.8 0.30000000000000004 -16.17 1.8 0.4 -16.28 1.8 0.5 -16.450000000000003 1.8 0.6000000000000001 -16.680000000000003 1.8 0.7000000000000001 -16.970000000000002 1.8 0.8 -17.320000000000004 1.8 0.9 -17.730000000000004 1.8 1.0 -18.200000000000003 1.8 1.1 -18.730000000000004 1.8 1.2000000000000002 -19.320000000000004 1.8 1.3 -19.970000000000002 1.8 1.4000000000000001 -20.680000000000003 1.8 1.5 -21.450000000000003 1.8 1.6 -22.280000000000005 1.8 1.7000000000000002 -23.170000000000005 1.8 1.8 -24.120000000000005 1.8 1.9000000000000001 -25.130000000000003 1.8 2.0 -26.200000000000003 1.8 2.1 -27.330000000000005 1.9000000000000001 0.1 -17.98 1.9000000000000001 0.2 -17.970000000000002 1.9000000000000001 0.30000000000000004 -18.02 1.9000000000000001 0.4 -18.130000000000003 1.9000000000000001 0.5 -18.3 1.9000000000000001 0.6000000000000001 -18.53 1.9000000000000001 0.7000000000000001 -18.82 1.9000000000000001 0.8 -19.17 1.9000000000000001 0.9 -19.580000000000002 1.9000000000000001 1.0 -20.05 1.9000000000000001 1.1 -20.58 1.9000000000000001 1.2000000000000002 -21.17 1.9000000000000001 1.3 -21.82 1.9000000000000001 1.4000000000000001 -22.53 1.9000000000000001 1.5 -23.3 1.9000000000000001 1.6 -24.130000000000003 1.9000000000000001 1.7000000000000002 -25.020000000000003 1.9000000000000001 1.8 -25.97 1.9000000000000001 1.9000000000000001 -26.980000000000004 1.9000000000000001 2.0 -28.05 1.9000000000000001 2.1 -29.18 2.0 0.1 -19.93 2.0 0.2 -19.92 2.0 0.30000000000000004 -19.97 2.0 0.4 -20.080000000000002 2.0 0.5 -20.25 2.0 0.6000000000000001 -20.48 2.0 0.7000000000000001 -20.77 2.0 0.8 -21.12 2.0 0.9 -21.53 2.0 1.0 -22.0 2.0 1.1 -22.53 2.0 1.2000000000000002 -23.12 2.0 1.3 -23.77 2.0 1.4000000000000001 -24.480000000000004 2.0 1.5 -25.25 2.0 1.6 -26.08 2.0 1.7000000000000002 -26.970000000000002 2.0 1.8 -27.92 2.0 1.9000000000000001 -28.930000000000003 2.0 2.0 -30.0 2.0 2.1 -31.13 2.1 0.1 -21.98 2.1 0.2 -21.970000000000002 2.1 0.30000000000000004 -22.02 2.1 0.4 -22.130000000000003 2.1 0.5 -22.3 2.1 0.6000000000000001 -22.53 2.1 0.7000000000000001 -22.82 2.1 0.8 -23.17 2.1 0.9 -23.580000000000002 2.1 1.0 -24.05 2.1 1.1 -24.58 2.1 1.2000000000000002 -25.17 2.1 1.3 -25.82 2.1 1.4000000000000001 -26.53 2.1 1.5 -27.3 2.1 1.6 -28.130000000000003 2.1 1.7000000000000002 -29.020000000000003 2.1 1.8 -29.97 2.1 1.9000000000000001 -30.980000000000004 2.1 2.0 -32.05 2.1 2.1 -33.18
splot `data3d.dat` notitle
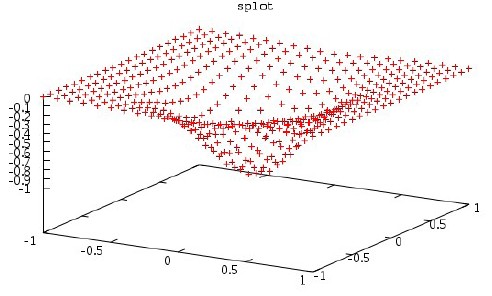
使用lines选项把每个点用线接连起来:
splot `data3d.dat` with lines notitle
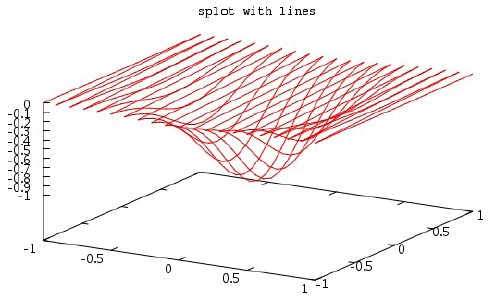
也可以通过dgrid3d指定用网格来显示:
set dgrid3d 50,50 set hidden3d replot
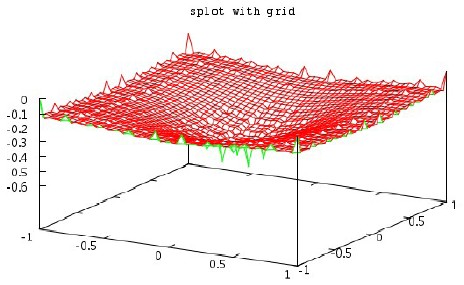
上面图里的网络与文件中的数值不同,原因是网格默认会对Z轴上的值做出平均。
通过splines禁止自动平均:
set dgrid3d splines set xlabel 'x' set ylabel 'y' set zlabel 'z' set title 'splot with splines grid' set ticslevel 0 set ztics -1, 0.5, 0 replot
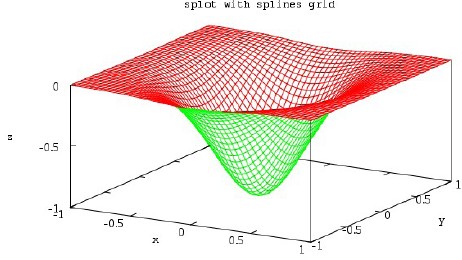
极坐标模式
极坐标模式绘图
-
set polar指定极坐标模式 -
默诵变量为
t,默认取值范围是\(0\)~\(2\pi\) -
set size ration 1指定高宽比为1
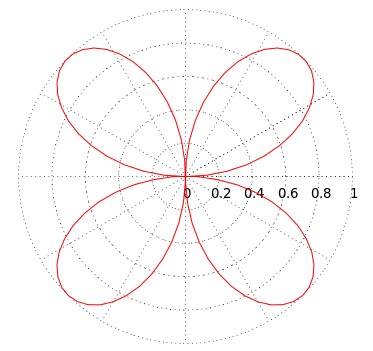
set polar set xrange [-1:1] set yrange [-1:1] set grid polar set size ratio 1 set xtics 0.2 set ytics 0.2 plot sin(2*t) notitle
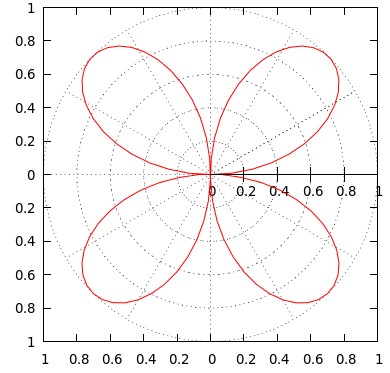
如果想要把方的线都去掉,可以做以下调整:
- 如果要去掉边框,可以设置边框线为宽为0。
- 把x轴和y轴的标注都改为白色的,这样就看不见了。
set border linewidth 0 set xtics textcolor rgbcolor 'white' set ytics textcolor rgbcolor 'white' replot
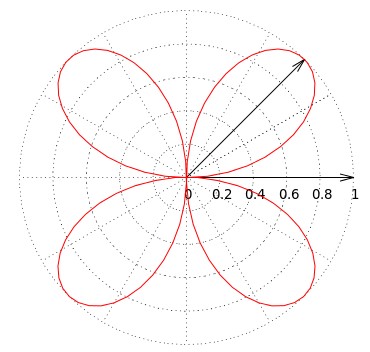
还可以加上两个箭头:
set arrow from 0,0 to 1,0 set arrow from 0,0 to 0.707,0.707 replot
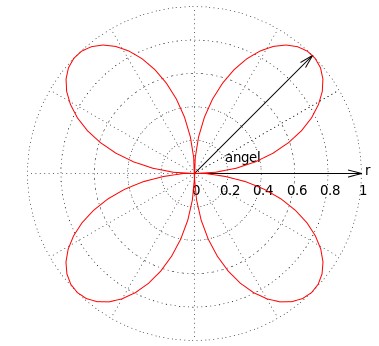
要指定的坐标上给加上注解「r」和「angel」:
set label 'angel' at 0.18,0.1 set label 'r' at 1.02,0.02 replot
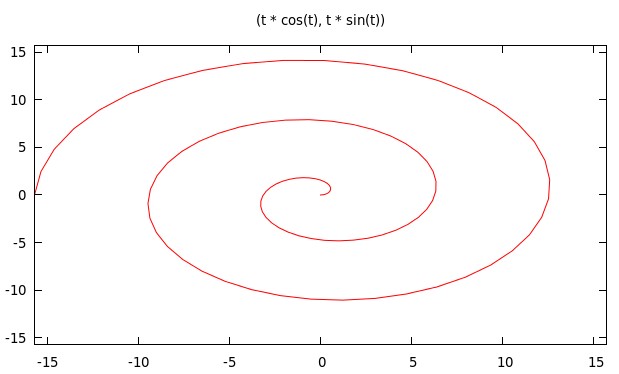
参数方程作图
-
set parametric指定为参数方程。 -
set size ration 1指定高宽比为1 -
曲线作图默认变量
t,默认范围\([-5, 5]\) -
曲面作图默认变量
u和t,默认范围\([-10, 10]\)
set parametric set trange [0 : 5 * pi] set xrange [-5 * pi : 5 * pi] set yrange [-5 * pi : 5 * pi] set size ration 1 set title '(t * cos(t), t * sin(t))' plot t * cos(t), t * sin(t) notitle
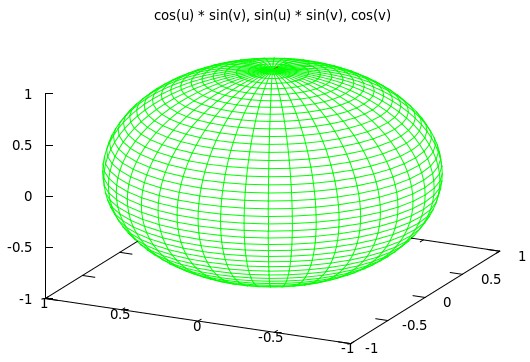
set parametric set urange [0:2*pi] set vrange [0:pi] set xrange [-1:1] set yrange [-1:1] set zrange [-1:1] set isosamples 45,45 set hidden3d set ticslevel 0 # 平移z轴 set view 60, 30, 1, 1.5 # 视角 set title 'cos(u) * sin(v), sin(u) * sin(v), cos(v)' splot cos(u) * sin(v), sin(u) * sin(v), cos(v) notitle