集合基础

集合的定义

元素

研究的对象，用小写字母表示。例如：\(a, b, c, d, \dots\)

集合

一些元素的总集，用大写字母表示。例如：\(A, B, C, D, \dots\)

集合的分类：无限集合、有限集合、空集（\(\phi\)）

常用的集合：

• 正整数：\(N^+\)或\(N^*\)。
• 自然数：\(N\)（包含正整数和\(0\)）
• 全体整数：\(Z\)（包含正整数和负整数）
• 有理数：\(Q\)
• 实数：\(R\)
• 复数：\(C\)

元素与集合之间的关系：

• 属于：\(a \in A\)
• 不属于：\(a \notin A\)

元素的特性：

1. 确定性：是否属于集合有明确的、可以量化的标准。
2. 无序性：集合中的元素不排序。只要元素相同，顺序不同的也算同一个集合。
3. 互异性：没有重复的元素。

集合的表示方法

列举法

• 列出所有元素：\(\{1, 2, 3, 4, 5\}\)
• 列出趋势与最后一个元素：\(\{1, 2, 3, 4, \dots, 5\}\)
• 无限集合：\(\{1, 2, 3, 4, 5, \dots\}\)

描述法

描述格式：\(\{x \in A | P(x)\}\)

也经常写为：\(\{x | P(x), x \in A \}\)

• \(x \in A\)：是代表元。
• \(P(x)\)：是代表元满足的性质。

默认情况下，\(x\)和\(y\)的范围都是实数，所以：

\[ \{x \in R | y = x^2 + 1\} \in R \]

可以简写为：

\[ \{x | y = x^2 + 1\} \]

例子，坐标的集合：\(\{ (x, y) | y = x^2 + 1 \}\)

例子，文字描述：\(\{2010年黄冈中学学生\}\)

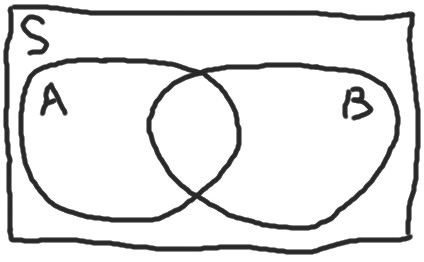
文氏图（Venn）

集合间的基本关系

• 子集：\(A \subseteq B\)，也可以写为\(B \subseteq A\)。
• 真子集：\(A \varsubsetneq B\)，且\(A\)与\(B\)不相同。
• 集合相等：\(A = B \Leftrightarrow A \subseteq B \quad and \quad B \subseteq A\)

• 空集（\(\phi\)）是任何集合的子集。列出一个集合的所有子集时「一定」要带上空集。
• 任何集合都是它自己的子集，即：\(A \subseteq A\)。

集合间的基本运算

• 交集：\(A \cap B = \{x | x \in A \quad and \quad x \in B\}\)
• 并集：\(A \cup B = \{x | x \in A \quad or \quad x \in B\}\)

运算性质

• 交换率：\(A \cap B = B \cap A\)，\(A \cup B = B \cup A\)
• 与自身：\(A \cap A = A\)，\(A \cup A = A\)
• 与空集：\(A \cap \phi = \phi\)，\(A \cup \phi = A\)
• \(A \cap B \subseteq A \subseteq A \cup B\)
• 若\(A \cap B = A\)，则\(A \subseteq B\)。反之也成立。
• 若\(A \cup B = A\)，则\(B \subseteq A\)。反之也成立。
• 容斥原理：用\(card(A)\)来表示集合\(A\)中元素的个数，则： \(card(A \cup B) = card(A) + card(B) - card(A \cap B)\)

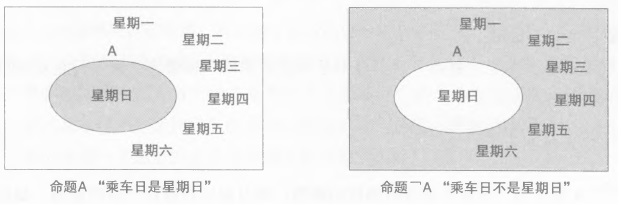
补集

设\(S\)表示全集，若\(A \subset S\)，则 \(C_SA = \{x | x \in S \quad and \quad x \not \in A\}\)

运算性质：

• \(C_S(C_SA) = A\)，\(C_SS = \phi\)，\(C_S\phi = S\)
• \(A \cap C_SA = \phi\)，\(A \cup C_SA = S\)
• \(C_S(A \cup B) = (C_SA) \cap (C_SB)\)
• \(C_S(A \cap B) = (C_SA) \cup (C_SB)\)