指数函数基础

幂函数

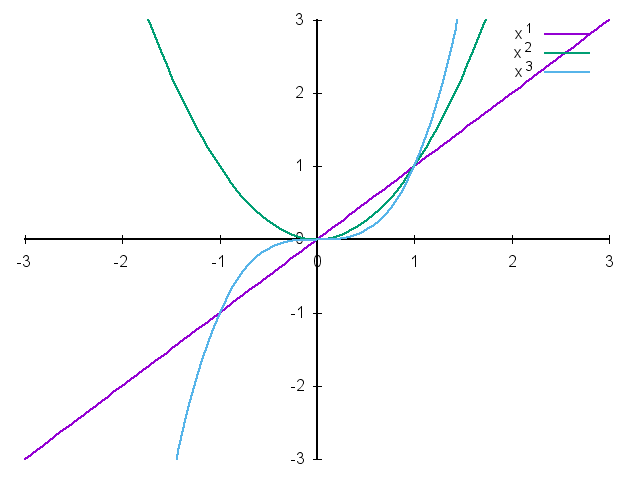
形式：\(y=x^a\)

• 幂函数在\((0, +\infty)\)都有定义，而且图像过点\((1, 1)\)。
• 当\(a \gt 0\)时，图像过原点，在\([0, +\infty)\)上递增。
  • 当\(0 \lt a \lt 1\)时，图像上凸；
  • 当\(a \gt 1\)时，图像下凸；
• 当\(a \lt 0\)时，图像不过原点（因为\(0\)作为分母无意义），在\((0, +\infty)\)上递减。 图像无限接近于\(x\)轴与\(y\)轴但不相交。

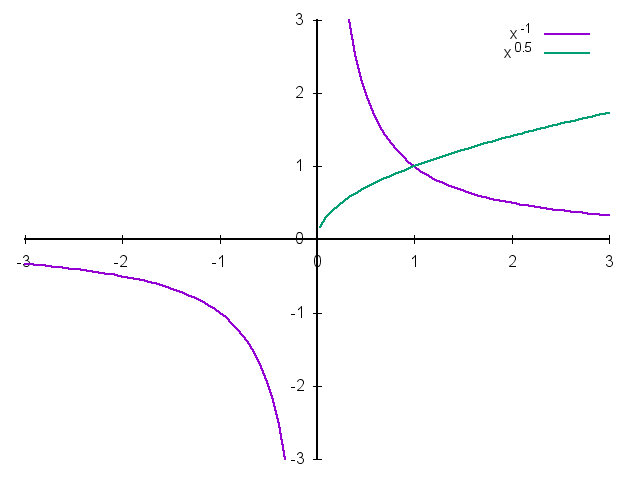
指数

整数指数

形式：\(a^n = a_1 \times a_2 \times a_3 \cdots a_n = v\)。 当\(n \in N_+\)而且\(n \gt 1\)，读作：\(a\)的\(n\)次幂。

• \(a\)为底。
• \(n\)为幂的指数。
• \(v\)为幂值。

当\(n\)等于\(0\)时：

\[ a^{0} = 1 \quad \quad (a \neq 0) \]

当\(n\)小于\(0\)时：

\[ a^{-n} = \frac{1}{a^n} \quad \quad (a \neq 0, n \in N_+) \]

运算性质

前提条件：\(a \gt 0\)且\(b \gt 0\)且\(m \in R\)且\(n \in R\)。

\[ a^m \times a^n = a^{m+n} \] \[ a^m \times a^{-n} = a^m \times \frac{1}{a^n} =\frac{a^m}{a^n} = a^{m-n} \] \[ (a^m)^n = a^{m \times n} \] \[ a^m \times b^m = (a \times b)^m \]

分数指数

如果存在实数\(x\)，使\(x^n = a\)且\(a \in R, n \in N, n \gt 1\)， 则把\(x\)叫作\(a\)的\(n\)次方根。

式子\(\sqrt[n]{a}\)叫作【根式】，\(a\)叫作被开放数，\(n\)叫作根指数。

\[ \begin{equation} \begin{split} x^n &= a \\ x &= \sqrt[n]{a} = a^{\frac{1}{n}} \end{split} \end{equation} \]

• 若\(n\)为奇数，\(a\)的\(n\)次方根记为：\(\sqrt[n]{a}\)
• 若\(n\)为偶数，\(a\)的\(n\)次方根记为：\(\pm\sqrt[n]{a}\)
• 正数\(a\)的正\(n\)次方根叫作\(a\)的\(n\)次算术根，负数没有偶次方根。
• 因为当\(n \gt 1\)且\(n \in N_+\)时，\(0^n=0\)；所以\(\sqrt[n]{0}=0\)。

前提条件：\(a \gt 0\)而且\(m,n \in N_+\)而且\(n \gt 1\)。

\[ a^{\frac{m}{n}} = \sqrt[n]{a^m} \] \[ a^{-\frac{m}{n}} = \frac{1}{\sqrt[n]{a^m}} \]

根恒等式

\[ \begin{equation} (\sqrt[n]{a})^n = a \end{equation} \]

当\(n\)为奇数时：

\[ \begin{equation} \sqrt[n]{a^n} = a \end{equation} \]

当\(n\)为偶数时：

\[ \begin{equation} \sqrt[n]{a^n}=|a|=\begin{cases} \begin{split} & a &, a \geq 0 \\ & -a \quad &, a \lt 0 \end{split} \end{cases} \end{equation} \]

分数指数的运算规则

正分数指数幂可定义为：

\[ \begin{equation} \sqrt[n]{a} = a^{\frac{1}{n}} \quad (a \gt 0) \end{equation} \] \[ \begin{equation} a^{\frac{m}{n}} = (\sqrt[n]{a})^m =\sqrt[n]{a^m} \quad (a \gt 0, n, m \in N_+) \end{equation} \]

负分数指数幂可定义为：

\[ \begin{equation} a^{-\frac{m}{n}} = \frac{1}{a^{\frac{m}{n}}} \quad (a \gt 0, n, m \in N_+) \end{equation} \]

整数指数幂推广到有理数指数幂

有理指数幂的运算性质：

\[ \begin{equation} a^ra^s = a^{r+s} \quad (a \gt 0, r, s, \in Q) \end{equation} \] \[ \begin{equation} (a^s)^r = a^{rs} = (a^r)^s \quad (a \gt0, r, s \in Q) \end{equation} \] \[ \begin{equation} (ab)^r = a^rb^r \quad (a \gt 0, b \gt 0, r \in Q) \end{equation} \]

无理数指数幂

对于无理数指数幂，这里不能给出严格的定义，但可以感性地通过把「用有理数逼近无理数」来理解。

例，对于\(5^{\sqrt{2}}\)：

\(\sqrt{2}\)的过剩近似值	\(5^{\sqrt{2}}\)的近似值	\(5^{\sqrt{2}}\)的近似值	\(\sqrt{2}\)的不足近似值
1.5	11.180,339,89	9.518,269,694	1.4
1.42	9.829,635,328	9.672,669,973	1.41
1.415	9.750,851,808	9.735,171,039	1.414
1.414,3	9.739,872,62	9.738,305,174	1.414,2
1.414,22	9.738,618,643	9.738,461,907	1.414,21
1.414,214	9.738,524,602	9.738,508,928	1.414,213
1.414,213,6	9.738,518,332	9.738,516,765	1.414,213,5
1.414,213,57	9.738.517.862	9.738,517,705	1.414,213,56
1.414,213,563	9.738.517.752	9.738,517,736	1.414,213,562
\(\cdots\)	\(\cdots\)	\(\cdots\)	\(\cdots\)

从上表中可以看出，当\(\sqrt{2}\)的近似值从过剩或是不足两个方向逼近 \(\sqrt{2}\)，\(5^\sqrt{2}\)的近似值也在从两边逼近。

所以可以得到结论：

1. 当指数幂为无理数时，指数有一个实数值。
2. 有理数指数幂的运算性质同样适用于无理数指数幂。

指数函数

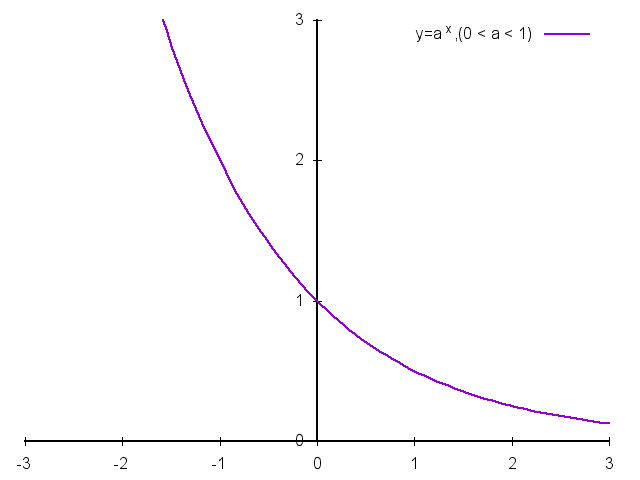
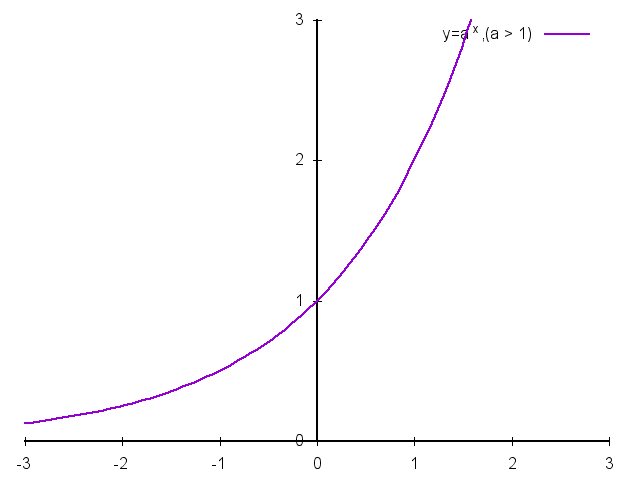
指数函数：\(y=a^x\)，\(a>0\)且\(a \ne 1\)。

\(a \gt 1\)时与\(0 \lt a \lt 1\)时函数的图像：

例子：

• \(y=\pi^x\)。是指数函数。
• \(y=(-4)^x\)。不是指数函数，因为底数为\(-4\)大于\(0\)。
• \(y=(2a-1)^x\)，\(a \gt \frac{1}{2}\)且\(a \ne 1\)。是指数函数。
• \(y=5^{2x^2+1}\)。不是指数函数，指数不是单独变量。

性质：

• 定义域：\(x \in R\)
• 值域：\(y \in (0, + \infty)\)
• 函数图像过点\((0, 1)\)。
• \(a \gt 1\)，函数在定义域\(R\)上单调递增。
• \(0 \lt a \lt 1\)，函数在定义域\(R\)上单调递减。

对数

若\(a^b=N\)，其中\(a \gt 0 \cap a \ne 1\)。则称\(b\)是以\(a\)为底的\(N\)的对数。 记作：\(b = \log_aN\)

• 在指数中\(N\)被称为「幂值」，在对数中称为「真数」。
• 在指数中\(b\)被称为「指数」，在对数中称为「对数」。

\[ \begin{equation} a^x = y \quad \longleftrightarrow \quad x=log_ay \end{equation} \]

	关系式	\(a\)	\(x\)	\(y\)
指数式	\(a^x = y\)	底数（\(a \gt 0, a \neq 1\)）	指数（\(x \in R\)）	幂（值）（\(y \in R_+\)）
对数式	\(x=log_ay\)	底数（\(a \gt 0, a \neq 1\)）	对数（\(x \in R\)）	真数（\(y \in R_+\)）

常用对数与自然对数

• 常用对数，以\(10\)为底：\(\log_{10}N\) 简写为 \(\lg N\)
• 自然对数，以\(e\)为底：\(\log_{e}N\) 简写为 \(\ln N\)

对数的性质与对数恒等式

对数恒等式：

因为\(a^b=N\)，设\(b=\log_aN\)，所以：

• \(a^{\log_aN}=N\)。这里的\(N\)是真数，所以必须大于\(0\)。
• \(\log_aa^N=N\)。这里的\(N\)是指数，所以可以是任何实数。

对数\(\log_aN\)的性质：

• 零和负数没有对数理，即：因为指数式\(a^b\)恒大于\(0\)，所以对数中的\(N\)恒大于\(0\)。所以\(0\)与负数是没有对数的。
• \(1\)的对数为\(0\)，即：因为在指数式中\(a^0=1\)，所以\(\log_a1=0\)。
• 底的对数为\(1\)，即：因为在指数式中\(a^1=a\)，所以\(\log_aa=1\)。

对数的运算性质

前提： \(a \gt 0\)，\(a \ne 1\)，\(M \gt 0\)，\(N \gt 0\)

\[ \begin{equation} \log_aM + \log_aN = \log_a(M \times N) \end{equation} \] \[ \begin{equation} \log_aM - \log_aN = \log_a(\frac{M}{N}) \end{equation} \] \[ \begin{equation} \log_aM^n = n \log_aM \quad \quad \text{其中} n \in R \end{equation} \]

对数的换底公式

对于：\(a \gt 0\)，\(a \ne 1\)，\(m \gt 0\)，\(m \ne 1\)，\(N \gt 0\)

\[ \log_aN = \frac{\log_mN}{\log_ma} \]

注：

\[ \begin{equation} \log_ba \times \log_ab = 1 \end{equation} \] \[ \begin{equation} \log_{a^m}b^n=\frac{n}{m}\log_ab \quad \quad \text{其中} \quad m,n \in R \text{并且} m \ne 1 \end{equation} \]

对数函数

指数函数与对数函数互为反函数，它们的图像关于直线\(y=x\)对称。

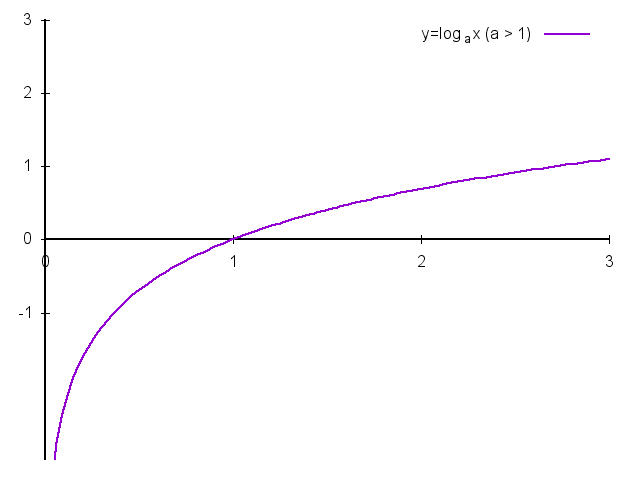
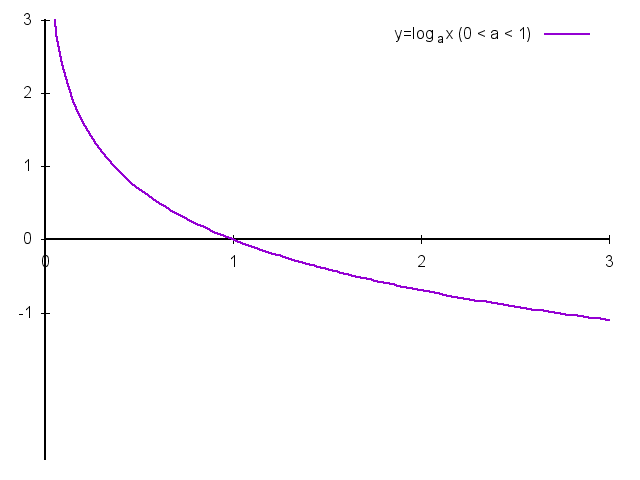
定义：\(y = \log_ax\)，其中\(a \gt 0\)并且\(a \ne 1\)。

• 定义域：\(x \in (0, + \infty)\)
• 值域：\(y \in R\)
• 必定过点\((1, 0)\)
• 当\(a \gt 0\)时函数单调递增；当\(0 \lt a \lt 1\)函数单调递减。

设\(y_1=\log_ax\)，\(y_2=\log_bx\)。其中a，b必须同时大于0或同时小于0：

• 当\(x \gt 1\)时，若\(a \gt b\)，则\(y_1 \lt y_2\)
• 当\(1 \lt x \lt 1\)时，若\(a \gt b\)，则\(y_1 \gt y_2\)

对数值的大小比较

• 如果底数相同，则按函数单调性（\(a \gt 1\)为增函数，\(0 \lt a \lt 1\)为减函数）。
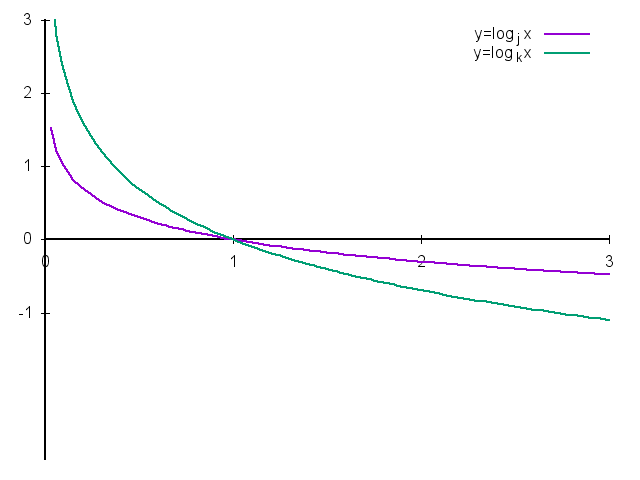
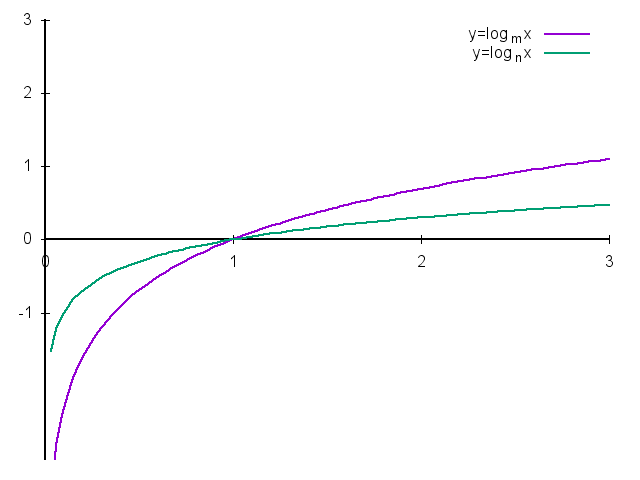
• 如果底数不同但真数相同，函数的底\(a\)越大，在\(x\)轴上方的部分越偏右。例，\(0 \lt j \lt k \lt 1 \lt m \lt n\)：

• 如果底数真数都不一样，通常引入中间变量来比较。