函数基础
基本概念
基本初等函数包括以下6种:
- 常值函数:\(y = c\)
- 指数函数:\(y = a^x\) 其中 \((a \gt 0 , a \neq 1)\)
- 对数函数:\(y = \log_a^x\) 其中 \((a \gt 0 , a \neq 1)\)
- 幂函数:\(y = x^a\) 其中 \((a \in R)\)
- 三角函数:正弦、余弦、正切、余切、正割、余割。
- 反三角函数:反正弦、反余弦、反正切、反余切、反正割(基本不用)、 反余割(基本不用)。
映射
对于非空数集\(A\)和\(B\),存在对应关系\(f\),使得: 集合\(A\)中的每个元素\(x\)都有唯一的元素\(y\)在集合\(B\)中与之对应, 则\(f\)为集合\(A\)到集合\(B\)的函数。
\[ f: A \mapsto B \]映射可以有【一对一】和【多对一】,但不能有【一对无】或是【一对多】。
函数
\[ \{y = f(x), x \in A\} \]- \(A\)到\(B\)的元素:\(y = f(x)\)
- \(x\)的范围为定义域:\(x \in A\)
- \(y\)的范围为值域:\(y \in B\)
函数定义域的描述方式
闭区间:
- \(\{x|a \le x \le b\}\),简写为:\([a, b]\)
开区间:
- \(\{x|a \lt x \lt b\}\),简写为:\((a, b)\)
半开半闭区间:
- \(\{x|a \le x \lt b\}\),简写为:\([a, b)\)
- \(\{x|a \lt x \le b\}\),简写为:\((a, b]\)
- \(\{x|x \ge a\}\),简写为:\([a, +\infty)\)
开区间特殊情况:
- \(\{x|x \lt a\}\),简写为:\((-\infty, a]\)
同一函数
如果两个函数定义域相同,且对应法则完全一致,称这两个函数为同一函数。
分段函数
\[ y=|x|=\begin{cases} \begin{equation} \begin{split} & x, & x \gt 0 \\ & 0, & x = 0 \\ & -x, \quad & x \lt 0 \end{split} \end{equation} \end{cases} \]复合函数
\[ y = f(g(x)) \]- 只有当外层函数\(f\)的定义域与内层函数\(g\)的值域的交集非空时才能构成复合函数。
- 复合函数的定义域是由外层函数的定义域、内层函数的值域、函数的定义域共同决定的。
函数的表示方法
- 列表法
- 图像法
- 解析法:用等式(即函数的解析式)描述变量关系。
函数解析式
例题:
按\(f(x) = x^2 + 1\),求\(f(2x+1)\):
解:
\[ \begin{split} f(x) &= x^2 + 1 \\ &= (2x+1)^2 + 1 \\ &= 4x^2 + 4x +2 \\ \end{split} \]例题:
按\(f(x+1) = x^2 + x\),求\(f(x)\):
解法一(拼接法):
\[ \begin{split} f(x) &= x^2 + x \\ &= (x+1)^2 - (x + 1) \\ &= x^2 - x \end{split} \]解法二(换元法): 设\(x+1=t\),则\(x=t-1\)
\[ \begin{split} f(x+1) &= x^2 + x \\ f(t) &= (t-1)^2 + (t-1) \\ f(t) &= t^2 - t \\ f(x) &= x^2 - x \end{split} \]例题:
按\(f(\sqrt{x}) = 3x - 2\sqrt{x}\),求\(f(x)\):
解法一(拼接法):
\[ \begin{split} f(\sqrt{x}) &= 3x - 2\sqrt{x} \\ &= 3(\sqrt{x})^2 - 2\sqrt{x} \\ \end{split} \]因为\(\sqrt{x} \ge 0\),所以\(\{x|f(x)=3x^2-2x, x \ge 0\}\)
解法二(换元法): 设\(\sqrt{x}=t\),则\(\{t|x=t^2, t \ge 0\}\)
\[ \begin{split} f(\sqrt{x}) &= 3x - 2\sqrt{x} \\ f(t) &= 3t^2 - 2t \\ f(x) &= 3x^2 -2x \quad 且 \quad x \ge 0 \end{split} \]例题:
按
\[ f(x) + 2f\Big(\frac{1}{x}\Big) = x \]求\(f(x)\):
解:令\(t=\frac{1}{x}\),则\(x=\frac{1}{t}\)。所以:
\[ \begin{split} f(x) + 2f\Big(\frac{1}{x}\Big) &= x \\ f\Big(\frac{1}{t}\Big) + 2f(t) &= \frac{1}{t} \end{split} \]再与原式联立,得到:
\[ \begin{cases} \begin{equation} \begin{split} f(x) + 2f\Big(\frac{1}{x}\Big) &= x \\ f\Big(\frac{1}{x}\Big) + 2f(x) &= \frac{1}{x} \end{split} \end{equation} \end{cases} \]解得:
\[ f(x) = \frac{2}{3x} - \frac{x}{3} \]函数的单调性
\(\{x|f(x), x \in I \}\),\(D \subset I\),\(x_1,x_2 \in D\) (函数\(f(x)\)定义域\(I\)的某个区间\(D\)中的任意两个变量\(x_1\)和\(x_2\)):
- 当\(x_1 \lt x_2\)时,恒有\(f(x_1) \lt f(x_2)\),则\(D\)为\(f(x)\)的递增区间。
- 当\(x_1 \lt x_2\)时,恒有\(f(x_1) \gt f(x_2)\),则\(D\)为\(f(x)\)的递减区间。
- 若\(f(x)\)在区间\(D\)中是递增或递减的,则称\(f(x)\)在区间\(D\)上有单调性, \(D\)为函数\(y=f(x)\)的单调区间。
定义法证明函数的单调性
例
证明\(y=x^3\)在定义域上是增函数。
解:设\(x_1,x_2 \in R\),且\(x_1 \lt x_2\),则:
\[ \begin{split} f(x_1)-f(x_2) &= x_1^3 - x_2^3 \\ &= (x_1 - x_2)(x_1^2 + x_2^2 + x_1x_2) \\ &= (x_1 - x_2)\Big[\Big(x_1 + \frac{x_2}{2}\Big)^2 + \frac{3}{4}x_2^2\Big] \lt 0 \end{split} \]\(\therefore f(x_1) \lt f(x_2)\),\(\therefore f(x)=x^3\)在\(R\)上是增函数。
例
证明\(f(x)=-\sqrt{x}\)在定义域上是减函数。
解:函数的定义域为\([0, +\infty)\),设\(0 \lt x_1 \lt x_2\)
\[ \begin{split} f(x_1)-f(x_2) &= (-\sqrt{x_1})-(-\sqrt{x_2}) = \sqrt{x_2}-\sqrt{x_1} \\ &= \frac{(\sqrt{x_2}-\sqrt{x_1})(\sqrt{x_2}+\sqrt{x_1})}{\sqrt{x_2}+\sqrt{x_1}} \\ &= \frac{x_2-x_1}{\sqrt{x_2}+\sqrt{x_1}} \end{split} \]\(\because x \le x_1 \lt x_2\),\(\therefore x_2-x_1 \gt 0\), \(\sqrt{x_2}+\sqrt{x_1} \gt 0\)。
\(\therefore f(x_1)-f(x_2)\),即\(f(x_1) \gt f(x_2)\)
\(\therefore f(x)=-\sqrt{x}\)在它的定义域\([0, +\infty)\)上是减函数。
函数的最大值、最小值
最大值
\(f(x)\)在定义域\(I\)中,存在实数\(M\)满足:
- 对于任意\(x \in I\),都有\(f(x) \le M\)。
- 对于任意\(x_0 \in I\),都有\(f(x_0) \le M\)。
则称\(M\)为\(f(x)\)的最大值。
最小值
\(f(x)\)在定义域\(I\)中,存在实数\(M\)满足:
- 对于任意\(x \in I\),都有\(f(x) \ge M\)。
- 对于任意\(x_0 \in I\),都有\(f(x_0) \ge M\)。
则称\(M\)为\(f(x)\)的最小值。
函数的奇偶性
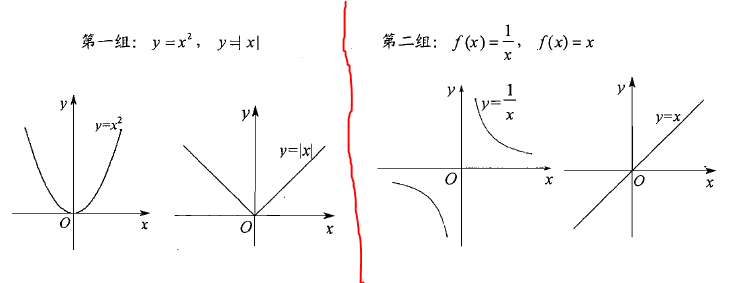
- 奇函数:关于原点对称。对于函数\(y=f(x)\)中任何一个\(x\),都存在\(-x \in D\),且 \(f(-x)=-f(x)\)。
- 偶函数:关于y轴对称。对于函数\(y=f(x)\)中任何一个\(x\),都存在\(-x \in D\),且 \(f(-x)=f(x)\)。
- 非奇非偶函数。
对于任何函数,有四种可以:
- 是非奇非偶函数。
- 仅为奇函数。
- 公为偶函数。
- 即是奇函数,又是偶函数。
即是奇函数又是偶函数的函数,其定义域恒为\(0\)。事实上对于定义域内任何一个\(x\), 由于\(f(-x)=f(x)\),且\(f(-x)=-f(x)\),则\(f(x)=-f(x)\),所以只有一个函数\(f(x)=0\)。
特性
若函数具备奇偶性:
- 定义域必定关于原点对称。
- 不是奇函数,就是偶函数。
以上两条有一条不满足,函数就是非奇非偶函数。
- 若\(f(x)=0\),则为即奇且偶函数。
- 奇函数在\(x=0\)时,\(f(x)\)一定也为\(0\)。
若\(f(x)\)与\(g(x)\)都是在区间\(I\)上的奇函数:
- \(f(x) \pm g(x)\)一定是奇函数。
- \(f(x) \times g(x)\)一定是偶,\(f(x) / g(x)\)在\(g(x)\)恒不为\(0\)时也为偶。
若\(f(x)\)与\(g(x)\)都是在区间\(I\)上的偶函数:
- \(f(x) \pm g(x)\)一定是偶函数。
- \(f(x) \times g(x)\)一定是偶,\(f(x) / g(x)\)在\(g(x)\)恒不为\(0\)时也为偶。
若\(f(x)\)在区间\(I\)上为奇函数;\(g(x)\)在区间\(I\)上为偶函数:
- \(f(x) \pm g(x)\)不可确定。
- \(f(x) \times g(x)\)一定是奇函数,\(f(x) / g(x)\)在\(g(x)\)恒不为\(0\)时为奇函数。