常用的函数

一元二次函数

二次函数解析式的几种形式

一般式

\[ \begin{equation} y = ax^2 + bx + c \end{equation} \]

\(a\)，\(b\)，\(c\)是常数，且\(a \neq 0\)。

顶点式：

\[ \begin{equation} y＝a(x-h)2+k \end{equation} \]

\(a,h,k\)为常数，\(a \neq 0\)。

任何一个二次函数通过配方都可以化为顶点式，抛物线的顶点坐标是\((h,k)\)：

• \(h=0\)时，抛物线\(y=ax^2+k\)的顶点在y轴上；
• 当\(k=0\)时，抛物线\(a(x-h)^2\)的顶点在x轴上；
• 当\(h=0\)且\(k=0\)时，抛物线\(y=ax^2\)的顶点在原点.

两根式：

\[ \begin{equation} y＝a(x-x1)(x-x2) \end{equation} \]

其中\(x1,x2\)是抛物线与x轴的交点的横坐标，即一元二次方程\(ax^2+bx+c=0\)的两个根， \(a \neq 0\)。

当抛物线与\(x\)轴有交点时，即对应二次方程有实数根\(x_1\)和\(x_2\)存在时，根据二次三项式的分解公式：

\[ \begin{equation} ax^2+bx+c＝a(x-x_1)(x-x_2) \end{equation} \]

二次函数可转化为两根式

一元二次函数图像

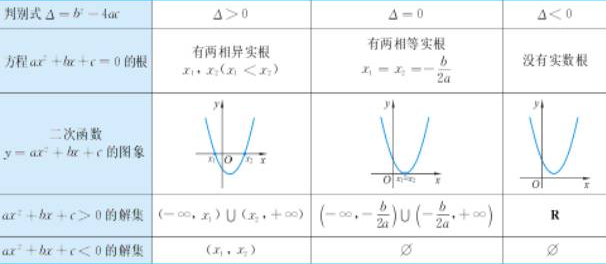
• 判别式：\(\Delta = b^2 -4ac\)
  1. \(\Delta \gt 0\)，有两个不相等的实根
  2. \(\Delta = 0\)，有两个相等的实根
  3. \(\Delta \lt 0\)，无实根
• 与\(y\)轴交点为：\((0,c)\)
• \(a>0\)开口向上；\(a<0\)开口向下
• 对称轴\(x=\frac{-b}{2a}\)
• \(a\)，\(b\)同号，对称轴在\(y\)轴左侧，反之，再\(y\)轴右侧
• 函数的顶点为：\((-b/2a,(4ac-b^2)/4a)\)

移动图像：

1. 函数向左移动\(d\)个单位，解析式为\(y=a(x+b/2a+d)^2+(4ac-b^2)/4a\)
2. 函数向上移动\(d\)个单位，解析式为\(y=a(x+b/2a)^2+(4ac-b^2)/4a+d\)

\[ \begin{equation} |x1-x2|= \sqrt{\frac{b^2-4ac}{|a|}} \end{equation} \]

一元二次函数顶点坐标

对于二次函数\(y=ax^2+bx+c\)，其顶点坐标为：

\[ \begin{equation} \Big(\frac{-b}{2a},\frac{4ac-b^2}{4a}\Big) \end{equation} \]

一元二次函数最值

一般来说，如果这个一元二次函数的定义域是\(R\)的话：

1. 函数开口向上，即\(a>0\)时，则没有最大值，只有最小值，即函数的顶点，可用函数的顶点公式来求。
2. 函数开口向上，即\(a<0\)时，则没有最小值，只有最大值，求法同上。

若该函数的定义域不是R的话：

1. 函数开口向上，即\(a>0\)时：
   • 当\(-b/2a\)在定义域内时，有最小值，再看定义域区间
     • 假设是闭区间\([m,n]\)，若\(\frac{-b}{2a} \gt \frac{n+m}{2}\)，则最大值是\(x=m\)时的函数值， 若\(\frac{-b}{2a} \lt \frac{n+m}{2}\)，则相反，若两者相同，则最大值即是端点值。
     • 当定义域区间是开区间\((m,n)\)时，则无最大值
     • 还有就是区间是半开半闭的情况时，即\([m,n)\)或\((m,n]\)时，按上面闭区间的方法计算，但若\(x\)取不到，则没有最大值
   • 当\(-b/2a\)不在定义域内时，
     • 假设是闭区间\([m,n]\),则最小值和最小值就是两个端点值，算一下再比较大小就行
     • 当定义域区间是开区间\((m,n)\)时，则无最大最小值
     • 当区间是半开半闭的情况，即\([m,n)\)或\((m,n]\)时，按上面闭区间的方法计算，关键是看能不能取到，但肯定是只有一个最值的

至于函数开口向下，即\(a \lt 0\) 的情况，上面的看懂了就会了

其实最方便的还是画个草图，分情况讨论一下就行了 ，算二次函数的最值问题只要不弄错定义域，情况分清楚，不讨论错还是很简单的

求抛物线的顶点、对称轴、最值的方法

配方法：将解析式化为\(y=a(x-h)^2+k\)的形式，顶点坐标(h,k)，对称轴为直线\(x=h\)，若\(a \gt 0\)，y有最小值，当\(x=h\)时，y最小值为k，若\(a \lt 0\)，y有最大值，当\(x=h\)时，y最大值为k.

公式法：直接利用顶点坐标公式求其顶点；对称轴是直线x＝- ,若a＞0，y有最小值，当x＝- 时，y最小值＝ ，若a＜0，y有最大值，当x＝- 时，y最大值＝ .