空间几何结构
空间直角坐标系
点\(P_1(x_1,y_1,z_1)\)与点\(P_2(x_2,y_2,z_2)\)之间的距离:
\[ P_1P_2=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2} \]常见空间几何结构
-
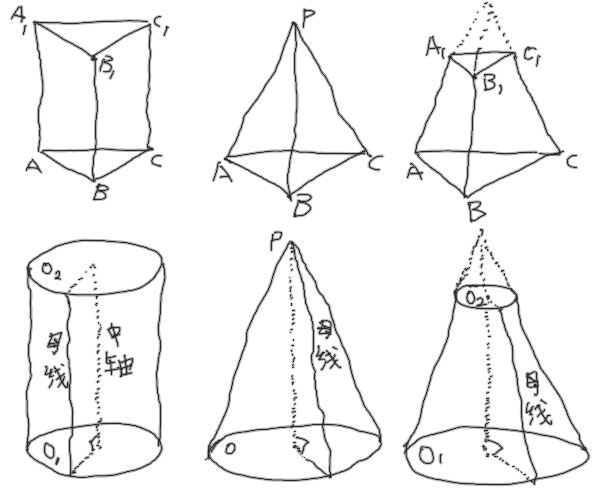
多面体:
- 棱柱(上下底面要平行的)。写法:从底面到顶面。例如:\(ABC - A_1B_1C_1\)
- 棱锥。写法:顶点到底。例如:\(P - ABC\)
- 棱台(上下底面要平行的)。写法:从底面到顶面。例如:\(ABC - A_1B_1C_1\)
-
旋转体:
- 圆柱(上下底面要平行的)。写法:从底面到顶面。例如:\(O_1 - O_2\)
- 圆锥。写法:从底面到顶面。例如:\(P - O\)
- 圆台(上下底面要平行的)。写法:从底面到顶面。例如:\(O_1 - O_2\)
- 球形:表示为\(O\)。
空间几何体的三视图
投影:中心投影、平等投影、正投影、斜投影。
三视图:正视图、侧视图、俯视图。
常见空间几何体的表面积与体积
圆柱体
\[ \begin{split} S_{\text{侧面积}} &= 2\pi{}rl \\ S_{\text{全面积}} &= 2\pi{}r(r+l) \\ V &= \pi{}r^2h \end{split} \]对于圆柱体来说,高\(h\)和母线\(l\)是一样的。
圆锥
母线标记为\(l\)。
\[ \begin{split} S_{\text{侧面积}} &= \pi{}rl \\ S_{\text{全面积}} &= \pi{}r(r+l) \\ V &= \frac{1}{3}\pi{}r^2h \end{split} \]圆台
- 母线标记为\(l\)。
- 上底半径标记为\(r_1\)。
- 下底半径标记为\(r_2\)。