Jade Dungeon

角与三角

任意角的概念与弧度制

角的概念与推广

角：一条射线绕端点从一个位置旋转到另一个位置。

角的三要素：顶点、始边、终边。

角的旋转方向：正角（逆时针方向）、零角、负角。

坐标轴系中讨论角：

角有顶点在原点，始边在$x$轴的非负半轴上；终边在哪一个象限，角就属于哪个象限。
终边在坐标轴的角不属于任何象限，称为【轴线角】。

弧度制

角度制

角度制把圆周分为360等分，一份对应1度。

弧度制

弧度制把长度等于半径（$r$）的圆弧（$l$）所对的圆心角记为一个弧度的角。

正角的弧度为正数，负角的弧度为负数，零角的弧度数为零。
任意一个已知的角$\alpha$的弧度的绝对值$|\alpha|=\frac{l}{r}$

圆周长与半径的关系是$2\pi{}r$，所以一个完整的圆有$360^\circ$：

\[ 360^\circ = 2 \cdot \pi \cdot rad \]

所以半圆$180^\circ$：

\[ 180^\circ = \pi \cdot rad \]

一个弧度就是：

\[ 1 \cdot rad = \Bigg\lgroup \frac{180}{\pi} \Bigg\rgroup ^ \circ \thickapprox 57.30^\circ = 57^\circ 18' \]

引入弧度制是为了把角的集合与实数的集合连接起来，可以用函数方式来对待三角函数。

弧度制与角度制的换算

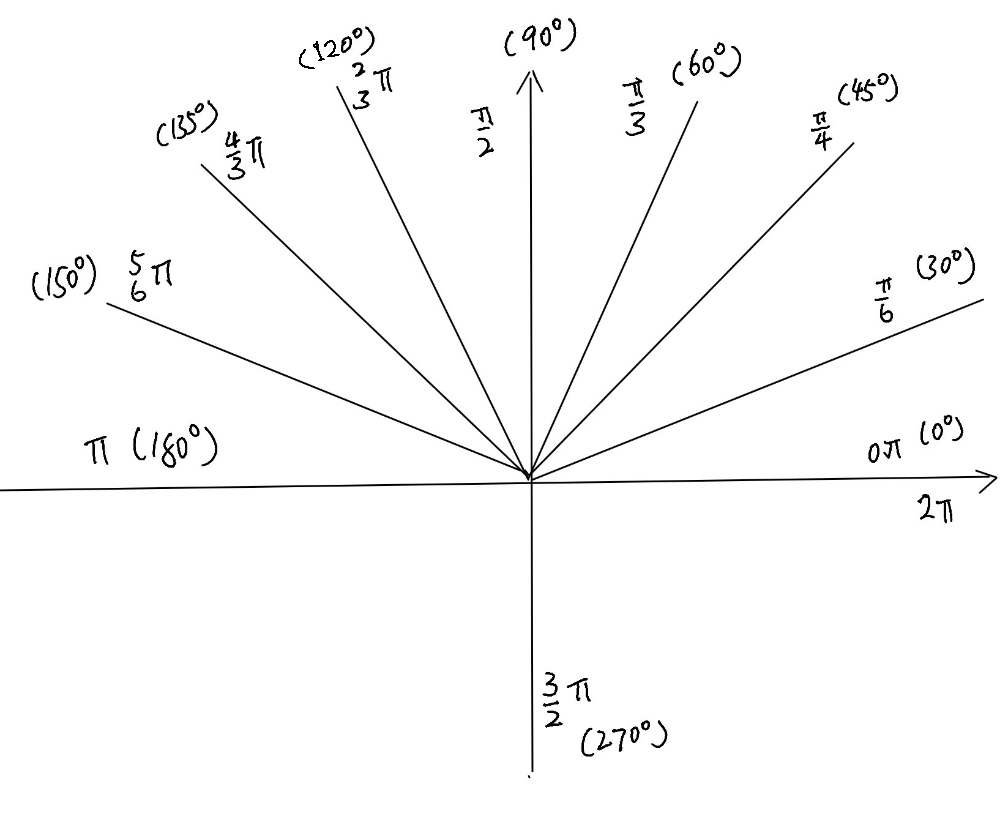
\[ \begin{split} 180^\circ &= \pi \cdot rad \\ 1 \cdot rad &= \Bigg\lgroup \frac{180}{\pi} \Bigg\rgroup ^ \circ \thickapprox 57.30^\circ = 57^\circ 18' \end{split} \]

一些特殊的角：

$特殊角的弧度与角度$

扇形中的计算公式

扇形的半径为$R$，圆心角为$\theta$弧度。计算弧长$l$：

\[ l = \theta R \]

计算面积$S$：

\[ S = \frac{1}{2}lR = \frac{1}{2}\theta R^2 \]

终边相同的角的集合

设任意角$\alpha$，所有与它终边相同的角（包括它自己）构成一个集合，记为：

\[ S=\Big\{\beta | \beta = \alpha + 2k\pi, k \in Z \Big\} \]

终边相同不一定角相等，但角相等一定终边相同。
终边相同的角有无数个，相差$2\pi$的整数倍。

小于$\frac{\pi}{2}$的角：

\[ \Big\{ \theta | \theta \lt \frac{\pi}{2} \Big\} \]

锐角：

\[ \Big\{ \theta | 0 \lt \theta \lt \frac{\pi}{2} \Big\} \]

第一象限的角：

\[ \Big\{ \theta | 2k\pi \lt \theta \lt 2k\pi + \frac{\pi}{2}, k \in Z \Big\} \]

第二象限的角：

\[ \Big\{ \theta | 2k\pi + \frac{\pi}{2} \lt \theta \lt 2k\pi + \pi, k \in Z \Big\} \]

第三象限的角：

\[ \Big\{ \theta | 2k\pi + \pi \lt \theta \lt 2k\pi + \frac{3\pi}{2}, k \in Z \Big\} \]

第四象限的角：

\[ \Big\{ \theta | 2k\pi + \frac{3\pi}{2} \lt \theta \lt 2k\pi + 2\pi, k \in Z \Big\} \]

任意角的三角函数

三角函数的定义

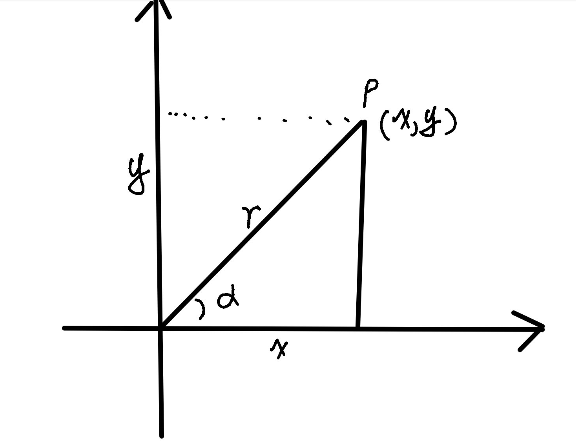
$任意角的三角函数$

正弦

正弦，定义域为$R$，值域$[-1, 1]$：

\[ \sin{\alpha} = \frac{y}{r} \]

$正弦$

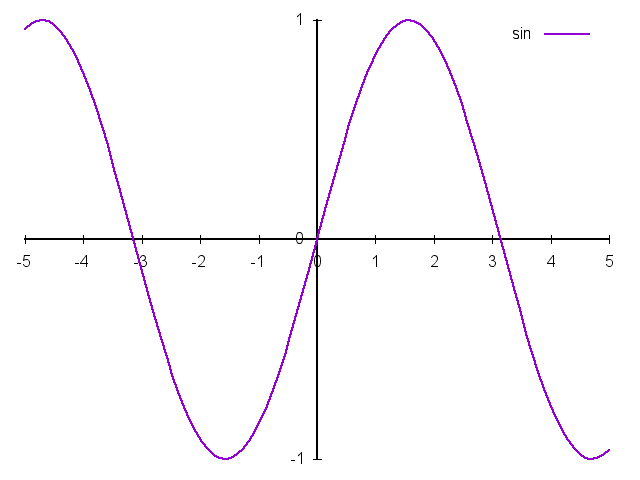
最小正周期$2\pi$
奇函数。
对称轴$x=\frac{\pi}{2}+k\pi, (k \in Z))$
对称中心$(k\pi, 0), (k \in Z)$
单调增区间$[-\frac{\pi}{2}+2k\pi, \frac{\pi}{2}+2k\pi], (k \in Z)$
单调减区间$[\frac{\pi}{2}+2k\pi, \frac{3\pi}{2}+2k\pi], (k \in Z)$

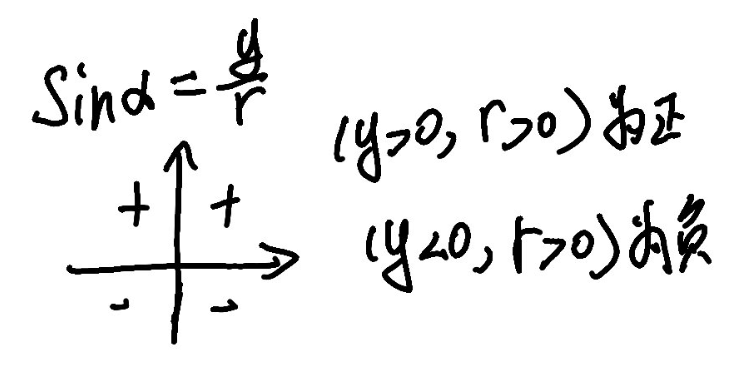
$正弦函数的符号$

余弦

余弦，定义域为$R$，值域$[-1, 1]$。：

\[ \cos{\alpha} = \frac{x}{r} \]

$余弦$

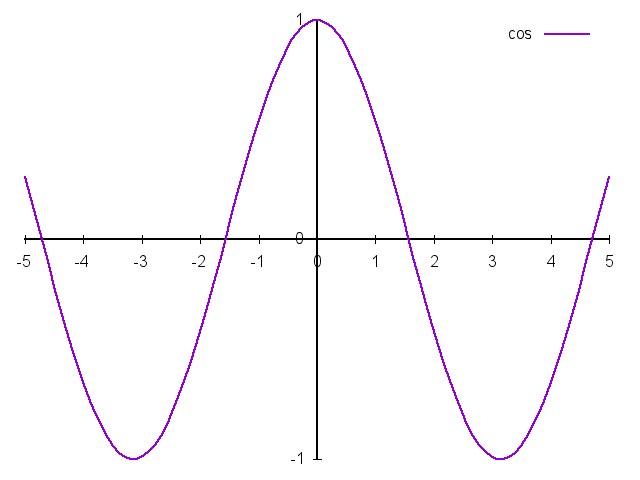
最小正周期$2\pi$
偶函数。
对称轴$x=k\pi, (k \in Z))$
对称中心$(\frac{\pi}{2}+k\pi, 0), (k \in Z)$
单调增区间$[-\pi+2k\pi, 2k\pi], (k \in Z)$
单调减区间$[2k\pi, \pi+2k\pi], (k \in Z)$

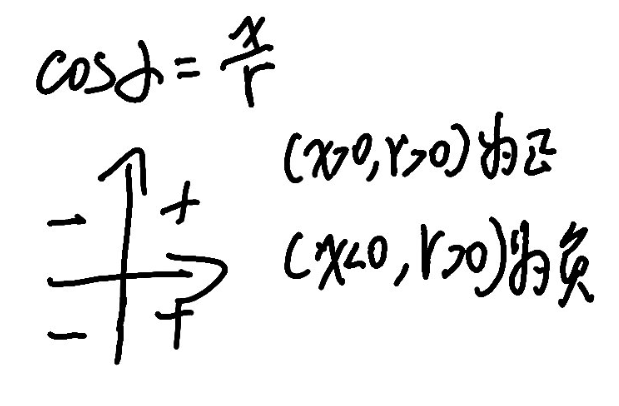
$余弦的符号$

正切

正切，定义域为$\{\alpha | \alpha \neq \frac{\pi}{2} + k\pi , k \in Z\}$，值域$R$：

\[ \tan{\alpha} = \frac{y}{x}, (x \neq 0) \]

$正切$

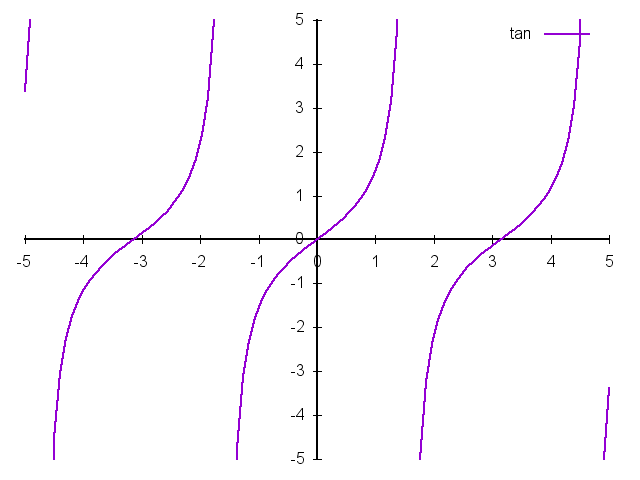
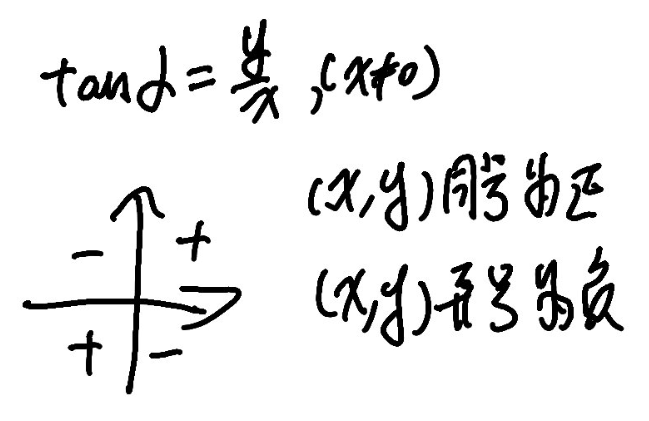
$正切的符号$

函数$y=A\sin(\omega x + \varphi)$的图像与性质

对于函数

\[ \begin{equation} y=A\sin(\omega x + \varphi), (x \in R) \end{equation} \]

与

\[ \begin{equation} y=A\cos(\omega x + \varphi), (x \in R) \end{equation} \]

其中$\cos, \omega, \varphi$是常量，且$A \neq 0, \omega \gt 0$。

基本性质

周期性

这两个函数的周期仅与自变量系数有关，最小正周期为$T=\frac{2\pi}{\omega}$

证明：

设$y=A\sin(\omega x + \varphi)$周期为$T$，则：

\[ \begin{split} f(x+T) &= f(x) \\ A\sin(\omega x + \omega T + \varphi) &= A\sin(\omega x + \varphi) \end{split} \]

又因为$y=\sin x$最小正周期为$2\pi$，所以

\[ \begin{split} \omega T &= 2\pi \\ T &= \frac{2\pi}{\omega} \end{split} \]

对称轴

对称轴方程为：

\[ \omega x + \varphi = \frac{\pi}{2} + k\pi , (k \in Z) \]

证明：$y=\sin{x}$对称轴为$x=\frac{\pi}{2}+k\pi$

对称中心

对称中心为：$(x_0, 0)$其中$\omega x_0 + \varphi = k\pi$，且$k \in Z$

证明：$y=\sin{x}$对称中心为$(k\pi,0)$

图形变换

从$y=\sin{x}$图象到$y=A\sin(\omega x + \varphi)+h$的图像变换。

步骤1：先$\varphi$，再$\omega$，再$A$，最后$h$
步骤2：先$\omega$，再$\varphi$，再$A$，最后$h$

单位圆与三角函数线

单位圆

单位圆是在直角坐标系中，以为原点$O$作为圆心的圆。
单位圆的半径记为一个单元。

$单位圆$

因为半径$r$是一个单元，所以把它记为$1$，可以得到：

$| MP | = | y | = | \sin{\alpha} |$
$| OM | = | x | = | \cos{\alpha} |$
$|AT| = |\tan{\alpha}|$

\[ | MP | = | y | = | \frac{y}{1} | = | \frac{y}{r} | = | \sin{\alpha} | \] \[ | OM | = | x | = | \frac{x}{1} | = | \frac{x}{r} | = | \cos{\alpha} | \] \[ \begin{split} \frac{|MP|}{|AT|} &= \frac{|OM|}{1} \\ \frac{|MP|}{|OM|} &= |AT| \\ |AT| &= \frac{|MP|}{|OM|} = \frac{|y|}{|x|} = |\tan{\alpha}| \end{split} \]

三角函数线

与单位圆有关的【有向】线段：

$\overline{MP}$为角$\alpha$正弦线。
$\overline{OM}$为角$\alpha$余弦线。
$\overline{AT}$为角$\alpha$正切线

三角函数基本关系与诱导公式

\[ \cos{x} = \sin(x+\frac{\pi}{2}) \]

同角三角函数基本关系

\[ \sin^{2}x + \cos^{2}x = 1 \] \[ \frac{\sin{x}}{\cos{x}} = \tan{x} \]

关系的关键在于【同角】，用什么形式来表示角【不重要】，比如：

\[ \sin^{2}4\alpha + \cos^{2}4\alpha = 1 \]

关系存在的前题是角要有意义，如：

\[ \frac{\sin{\alpha}}{\cos{\alpha}} = \tan{\alpha} , \Big\{\alpha | \alpha \notin \frac{\pi}{2} + k\pi, k \in Z \Big\} \]

两个基本关系还可以推导出变形：

\[ \cos{\alpha} = \pm\sqrt{1 - \sin^{2}\alpha} \] \[ \sin^{2}\alpha = 1 - \cos^{2}\alpha \] \[ \cos^{2}\alpha = 1 - \sin^{2}\alpha \] \[ (\sin\alpha \pm \cos\alpha)^2 = 1 \pm 2\sin\alpha\cos\alpha \] \[ \frac{\sin{\alpha}}{\tan{\alpha}} = \cos{\alpha} \]

等等等……

常用角的三角函数值

角$\alpha$	$0$	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$	$\frac{2\pi}{3}$	$\frac{3\pi}{4}$	$\frac{5\pi}{6}$	$\pi$	$\frac{3\pi}{2}$	$2\pi$
$\sin{\alpha}$	$0$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$-1$	$0$
$\cos{\alpha}$	$1$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	$0$	$-\frac{1}{2}$	$-\frac{\sqrt{2}}{2}$	$-\frac{\sqrt{3}}{2}$	$-1$	$0$	$1$
$\tan{\alpha}$	$0$	$\frac{\sqrt{3}}{3}$	$1$	$\sqrt{3}$	不存在	$-\sqrt{3}$	$-1$	$-\frac{\sqrt{3}}{3}$	$0$	不存在	$0$

三角函数诱导公式

简单地说就是【奇变偶不变，符号看象限】。对于角度$k\cdot\frac{\pi}{2} + \alpha$，

如果$k$为偶数，函数名不变；为奇数则在正弦与余弦之间转变。
符号按角度所在的象限，对应的函数象限变换来决定。

具体可以写成6个公式。

公式一：终边相同的角的同一三角函数的值相等。

\[ \begin{equation} \begin{split} \sin(\alpha + 2k\pi) &= \sin\alpha \\ \cos(\alpha + 2k\pi) &= \cos \alpha \\ \tan(\alpha + 2k\pi) &= \tan \alpha \quad \quad (k \in Z) \end{split} \end{equation} \]

公式二：

\[ \begin{equation} \begin{split} \sin(\alpha + pi) &= -& \sin \alpha \\ \cos(\alpha + pi) &= -& \cos \alpha \\ \tan(\alpha + pi) &= & \tan \alpha \end{split} \end{equation} \]

公式三：

\[ \begin{equation} \begin{split} \sin(-\alpha) &= -\sin\alpha \\ \cos(-\alpha) &= -\cos\alpha \\ \tan(-\alpha) &= -\tan \alpha \end{split} \end{equation} \]

公式四：

\[ \begin{equation} \begin{split} \sin(\pi-\alpha) &= & \sin\alpha \\ \cos(\pi-\alpha) &= - & \cos\alpha \\ \tan(\pi-\alpha) &= - & \tan \alpha \end{split} \end{equation} \]

公式五：

\[ \begin{equation} \begin{split} \sin\Big(\frac{\pi}{2}-\alpha\Big) &= \cos \alpha \\ \cos\Big(\frac{\pi}{2}-\alpha\Big) &= \sin \alpha \end{split} \end{equation} \]

公式六：

\[ \begin{equation} \begin{split} \sin\Big(\frac{\pi}{2}+\alpha\Big) &= & \cos \alpha \\ \cos\Big(\frac{\pi}{2}+\alpha\Big) &= -& \sin \alpha \end{split} \end{equation} \]

根据公式一、二、三、四把任意角转为锐角三角函数，一般步骤为：

任意负角三角函数用公式一或三转为任意正角三角函数
任意正角三角函数用公式一转为 $0 ~ 2\pi$的三角函数
$0 ~ 2\pi$的三角函数用公式二或四转为锐角三角函数

角\(\alpha\)	\(0\)	\(\frac{\pi}{6}\)	\(\frac{\pi}{4}\)	\(\frac{\pi}{3}\)	\(\frac{\pi}{2}\)	\(\frac{2\pi}{3}\)	\(\frac{3\pi}{4}\)	\(\frac{5\pi}{6}\)	\(\pi\)	\(\frac{3\pi}{2}\)	\(2\pi\)
\(\sin{\alpha}\)	\(0\)	\(\frac{1}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{3}}{2}\)	\(1\)	\(\frac{\sqrt{3}}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{1}{2}\)	\(0\)	\(-1\)	\(0\)
\(\cos{\alpha}\)	\(1\)	\(\frac{\sqrt{3}}{2}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{1}{2}\)	\(0\)	\(-\frac{1}{2}\)	\(-\frac{\sqrt{2}}{2}\)	\(-\frac{\sqrt{3}}{2}\)	\(-1\)	\(0\)	\(1\)
\(\tan{\alpha}\)	\(0\)	\(\frac{\sqrt{3}}{3}\)	\(1\)	\(\sqrt{3}\)	不存在	\(-\sqrt{3}\)	\(-1\)	\(-\frac{\sqrt{3}}{3}\)	\(0\)	不存在	\(0\)