基础

余数

分组

问题：今天是周日，请问1亿天后是周几？

答：用余数的分组功能可以快速地回答。

\[ 100000000 \div 7 = 14285714 余 2 \]

规律寻找

大数字取余

但如果数字太大，通过直接取余就不太现实，比如：

今天是周日，求\(10^{100}\)后是周几？这时需要另外找规律：

公式	余
\(1 \div 7\)	1
\(10 \div 7\)	3
\(100 \div 7\)	2
\(1000 \div 7\)	6
\(10000 \div 7\)	4
\(100000 \div 7\)	5
\(1000000 \div 7\)	1
\(10000000 \div 7\)	3
\(100000000 \div 7\)	2
\(1000000000 \div 7\)	6
\(10000000000 \div 7\)	4
\(100000000000 \div 7\)	5

每加6个0星期数就循环。

\[ 100 \div 6 = 16 余 4 \]

所以\(10^{100}\)天后是周四。

大数字大指数

求\(1234567^{987654321}\)的个位数？

数字太大不能直接计算，因为只要个位数，从个位上找规律。在这里，个位是7：

1234567^0	1
1234567^1	7
1234567^2	9
1234567^3	3
1234567^4	1
1234567^5	7
1234567^6	9
1234567^7	3
1234567^8	1
1234567^9	7

发现循环周期为4。那么\(987654321 \div 4\)余\(1\)，\(4\)次方对应的是\(7\)。

总结

运用余数，把大数字化为小数字。

奇偶校验

通过奇偶校验位（parity bit）来检查奇偶性（parity）也是余数应用的场景之一。

奇偶校验例子：恋人问题

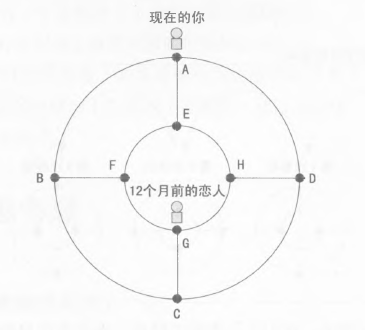
有A到H八个村子，位置和道路连接如上图。12个月前恋人的位置在G，每个月随机移动 一次。问现在恋人在A处的概率。

12个月移动12次，先试找规律：

1	C、F、H
2	B、D、E、G
3	A、C、F、H
4	B、D、E、G
5	A、C、F、H
6	B、D、E、G
7	A、C、F、H
8	B、D、E、G
9	A、C、F、H
10	B、D、E、G
11	A、C、F、H
12	B、D、E、G

可以看到从2开始出现重复，偶数次移动是不会出现在A的，所以概率为0。

在这个问题中，用不着考虑移动的线路，只要考虑可以到达的位置：

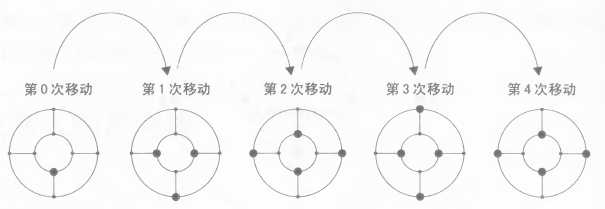
而在这个问题中，奇数和偶数可达的点是不重复的。满足排他性与完整性：

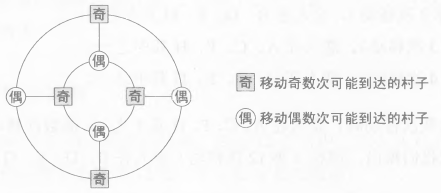
本题也是奇偶校验的一个例子。

奇偶校验例子：草席铺地

长方形草席能不能正好铺满地？

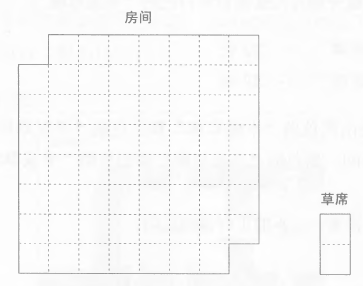
以半张正方形来算，面积上是正好都是62。但62是偶数，不能用奇偶性来判断。

加上颜色，可以看到30黑，32白：

所以不能。

奇偶校验例子：哥尼斯堡七桥问题

地图与抽象的路线逻辑图（Graph）：

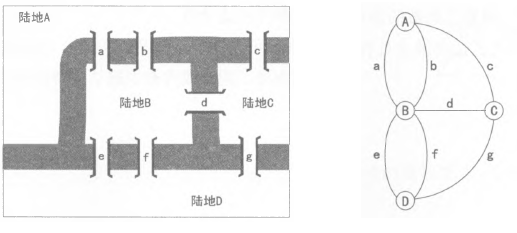
• 一次走完七座桥，不重复也不遗漏。
• 可以重复经过同一块陆地。
• 不用回到起点。

图论的开山鼻祖欧拉（Lenhard Euler）已经解决了这个问题：

• 度：图中一个顶点路线被叫作「度」
• 偶顶点：度数为偶数
• 奇顶点：度数为奇数

这个问题中要一次经过所有的线，所以：

• 进入一个顶点，减掉这个顶点的一个度；
• 同样离开一个顶点也要减一个度；

这样可以推论出：

• 所以每经过一个顶点，都要减少两个度（一进一出）。这样顶点的奇偶性不变。
• 离开起点与到达终点条减少一个度。会改变奇偶性。

再推论出：

• 如果起点和终点是同一个点，那么图中所有的顶点都要是偶顶点。
• 如果起点和终点非同一个点，那么图中只有起点和终点是奇顶点。

回到哥尼斯仲堡七桥问题，一次走全的条件：「所有顶点都是偶顶点，或有两个奇顶点。」

从图中看出奇顶点有4个，所以不能一次走全。

数学归纳法

数学归纳法的步骤

数学归纳法是证明：「断言对于0以上的所有整数都成立」。常见形式用数学归纳法来证明：

断言\(P(n)\)对\(0\)以上的所有整数\(n\)都成立。

1. 步骤1：证明\(P(0)\)成立。即当\(k = 0\)时，断言\(P(0)\)成立。这步被称为基底（base）。
2. 步骤2：证明不论\(k\)为\(0\)以上的哪个整数，若\(P(k)\)成立，则\(P(k+1)\)也成立。这步 被称为归纳（induction）。

例：高斯求和

把高斯求和断言记为\(G(n)\)，则表示为：

\[ 0 + 1 + 2 + 3 + \cdots + n = \frac{(n + 1) \times n}{2} \]

步骤1：基底证明

证明G(0)成立。

\[ \begin{equation} \begin{split} 0 &= 0 \frac{(0 + 1) \times 0}{2} &= 0 \end{split} \end{equation} \]

都是0，步骤1证明完毕。

步骤2：归纳证明

证明当\(k\)为\(0\)以上任一整数时，「若\(G(k)\)成立，则\(G(k+1)\)也成立」。

设\(G(k)\)成立，则以下等式成立：

\[ 0 + 1 + 2 + 3 + \cdots + k = \frac{(k + 1) \times k}{2} \]

要证明\(G(k+1)\)成立：

\[ 0 + 1 + 2 + 3 + \cdots + k + (k + 1) = \frac{((k + 1) + 1) \times (k + 1)}{2} \]

可以看到左右相等，从\(G(k)\)到\(G(k+1)\)推导成功，步骤2成功。

例：奇数的和

证明奇数的和等于数的平方。

即断言\(Q(n)\)对于\(1\)以上的所有整数都成立。断言\(Q(n)\)为：

\[ 1 + 2 + 3 + \cdots + (2 \times n - 1) = n^2 \]

例如：

• \(Q(1): 1 = 1\)
• \(Q(2): 1 + 3 = 2^2\)
• \(Q(3): 1 + 3 + 5 = 3^2\)
• \(Q(4): 1 + 3 + 5 + 7 = 4^2\)

\[ \] \[ \]

指数

指数定义

指数（exponent）

\[ \begin{equation} \begin{split} 10^{+3} &= 1 \times 10 \times 10 \times 10 \\ 10^{+2} &= 1 \times 10 \times 10 \\ 10^{+1} &= 1 \times 10 \\ 10^{0} &= 1 \\ 10^{-1} &= 1 \div 10 \\ 10^{-2} &= 1 \div 10 \div 10 \\ 10^{-3} &= 1 \div 10 \div 10 \div 10 \\ \end{split} \end{equation} \]

指数与进制

以十进制为例：

\[ a_n \times 10^n + a_{n-1} \times 10^{n-1} + \cdots + a_2 \times 10^2 + a_1 \times 10^1 + a_0 \times 10^0 \]

第\(k\)位可以表示为：\(a_k \times 10^k\)

指数乘法

\[ N^a \times N^b = N^{a + b} \\ \]

注意：\((N \neq 0)\)

勾股定理

Elo积分系统

当前积分（\(R\)）

一场比赛中的两个选手\(A\)与\(B\)，他们的当前积分分别为\(R_A\)和\(R_B\)。 对于一个第一次参加比赛的新人，各项比较给出的起始分数一般在\(1300\)到\(1600\)之间。

期望得分（\(E\)）

两位选手在比赛后应该得到的分数分别为\(E_A\)和\(E_B\)， 如果积分低的选手胜过了积分高的选手，那么应该获得更高的分数，而反之，则应更低， 这就是期望值的作用。期望值由以下公式计算：

\[ E_A = \frac{1}{1 + 10^{(R_B-R_A)/400}} \] \[ E_B = \frac{1}{1 + 10^{(R_A-R_B)/400}} \]

在这里400是一个常数，直观意义是想象我们这么定义一个人的战斗力： 任意两个人的战斗力之比就是他们之间比赛的胜率之比。 则那个常数为400时，两个战斗力相差10倍的人的elo rating相差400。

显然地，这个系统把战斗力取了对数，有效避免了《龙珠》里战斗力指数级上升的问题：

• 战斗力只有5的渣渣！ 相当于： elo rating只有1500的渣渣！
• 我的战斗力已经超过9000了！ 相当于： 我的elo rating超过了2800！（elo rating相差1300意味着战斗力相差1800倍）

胜负得分（\(S\)）

两个人比赛的胜负分别用\(S_A\)和\(S_B\)来表示，胜方为\(1\)，平局为\(0.5\)， 败方为\(0\)。比如：选手\(A\)胜出，则\(S_A=1, S_B=0\)。

新积分（\(R'\)）

这样，在比赛后，两个的新积分分别用\(R'_A\)和\(R'_B\)来表示：

\[ R'_A = R_A + (S_A - E_A) \]

K-value

实际应用中，一般会加上一个 K-value 对最终得分做出调整。 美国国际象棋联盟（USCF）的排名中，主要采用三级制，根据参赛者的实力值， 分成三个领域来决定K-value：

\[ K=\begin{cases} \begin{split} & 32 & \quad \text{ if } \quad 0 \le R \le 2099 \\ & 24 & \quad \text{ if } \quad 2100 \le R \le 2399 \\ & 16 & \quad \text{ if } \quad 2400 \le R \end{split} \end{cases} \]

为甚么业余级别的K-value需要高一点呢？

有一种说法是避免偶发性的失算，例如一个人的实力值约有2500， 但初始实力值是1600的话，升级至应有积分便需要对赛很多局。 调整K-value的话能加速达到应有的等级领域。而另一个说法是， 入门者的实力变化可能很急速，而相对来说专业级的稳定性较好……

为了让刚加入系统的高手尽快得到应有的评级， 世界国际象棋联盟（FIDE）索性让新加入者使用一个较高的K-value， 在30局过后才降回一般水平。FIDE对K值的设定如下：

• 首30局，K-value为25；
• 实力值不足2400的，K-value为15；
• 实力值到达2400并已进行超过30局的，K-value为10。以后K-value不会再改变。