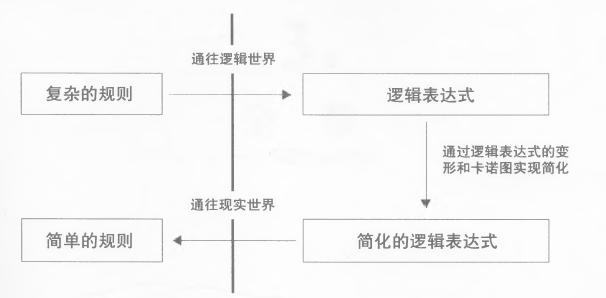
逻辑
逻辑基础
逻辑操作
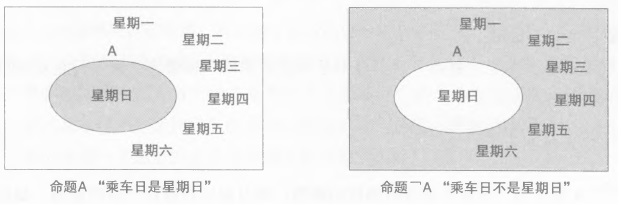
逻辑非
\[ \lnot A (not A) \]真值表:
| A | \(\lnot A\) | \(\lnot \lnot A\) |
|---|---|---|
| true | false | true |
| false | true | false |
文氏图:
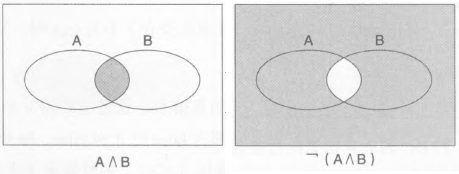
逻辑与
\[ A \land B (A and B) \]真值表:
| \(A\) | \(B\) | \(A \land B\) | \(\lnot (A \land B)\) |
|---|---|---|---|
| true | true | true | false |
| true | false | false | true |
| false | true | false | true |
| false | false | false | true |
文氏图:
逻辑或
\[ A \lor B (A or B) \]真值表:
| \(A\) | \(B\) | \(A \lor B\) |
|---|---|---|
| true | true | true |
| true | false | true |
| false | true | true |
| false | false | false |
文氏图:

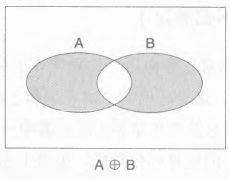
异或
\[ A \oplus B \]真值表:
| \(A\) | \(B\) | \(A \oplus B\) |
|---|---|---|
| true | true | false |
| true | false | true |
| false | true | true |
| false | false | false |
文氏图:
相等
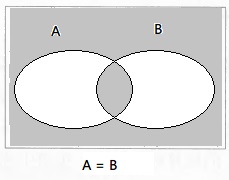
\[ A = B \]真值表:
A与B同为true和同为false的地方。
| \(A\) | \(B\) | \(A = B\) |
|---|---|---|
| true | true | true |
| true | false | false |
| false | true | false |
| false | false | true |
文氏图:
蕴涵
(缺少)
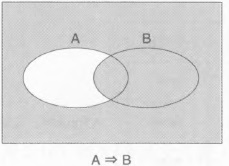
\[ A \Rightarrow B \]真值表:
| \(A\) | \(B\) | \(A \Rightarrow B\) |
|---|---|---|
| true | true | true |
| true | false | false |
| false | true | true |
| false | false | true |
文氏图:
除了「是A但不是B的地方」,其他都是。
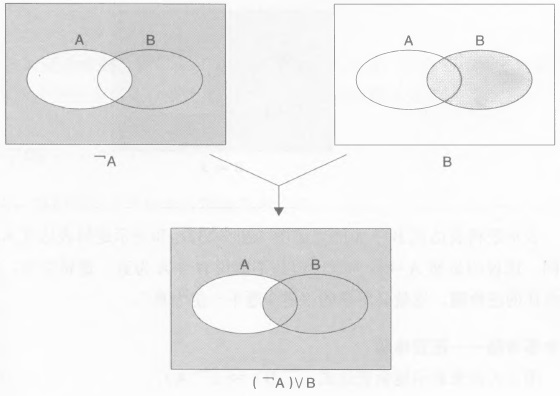
两个变量的逻辑组合
| \(A\) | true | true | false | false | |
| \(B\) | true | false | true | false | |
| 0 | alwars false | false | false | false | false |
| 1 | \(A \land B\) | true | false | false | false |
| 2 | \(A \land (\lnot B)\) | flase | true | false | false |
| 3 | \(A\) | true | true | false | false |
| 4 | \((\lnot A) \land B \) | false | false | true | false |
| 5 | \(B\) | true | false | true | false |
| 6 | \(\lnot(A = B)\) | false | true | true | false |
| 7 | \(A \lor B\) | true | true | true | false |
| 8 | \(\lnot (A \lor B)\) | false | false | false | true |
| 9 | \(A = B\) | true | false | false | true |
| 10 | \(\lnot B\) | true | true | true | true |
| 11 | \(A \lor (\lnot B)\) | true | true | false | true |
| 12 | \(\lnot A\) | false | false | true | true |
| 13 | \((\lnot A) \lor B\) | true | false | true | true |
| 14 | \(\lnot(A \lor B)\) | false | true | true | true |
| 16 | always true | true | true | true | true |
如果把上面的true改为1,false改为0,那正好对应前面数字的二进制形式。
命题(proposition)
是能判断对与错的陈述句。
真命题
命题正确。
假命题
命题错误。
逆命题
\[ A \Rightarrow B \]的逆命题是:
\[ B \Rightarrow A \]相当于:
\[ (\lnot B) \lor A \]文氏图:
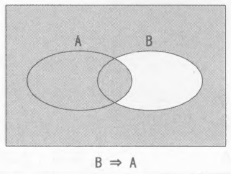
从图中就可见\(A \Rightarrow B\)不同于\(B \Rightarrow A\)。 所以命题为真逆命题不一定为真。
逆否命题
\[ A \Rightarrow B \]的逆否命题是:
\[ (\lnot B) \Rightarrow (\lnot A) \]相当于:
\[ (\lnot A) \lor B \]文氏图:
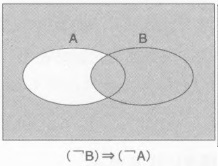
从图中就可见\(A \Rightarrow B\)相等于\((\lnot B) \Rightarrow (\lnot A)\)。 所以命题为真,逆否命题一定为真。
边界值
- 排他性
- 不能有重叠的范围,表示规则不存在矛盾之处。
- 完整性
- 不能有遗漏的范围,表示规则在所有情况下都适用。
边界要同时具有「完整性」与「排他性」。
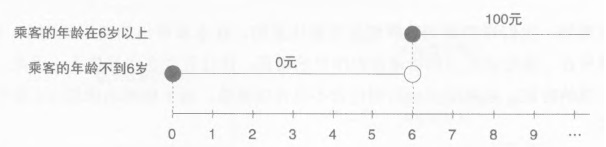
如果重复就不满足排他性:

如果遗漏就不满足完整性:
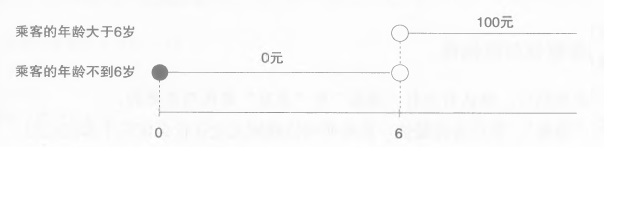
D Morgan 定理
\begin{equation} \begin{split} \lnot(A \land B) &= (\lnot A) \lor (\lnot B) \\ \lnot(A \lor B) &= (\lnot A) \land (\lnot B) \end{split} \end{equation}
简单地说:拆开非操作括号,里面的与和非反一下。
卡诺图
卡诺图把所有true、false组合以二维表展示,以寻找简化表示的方式。
例:二灯游戏
规则:机器上有一绿一黄两个灯,在以下三种情况,要按下按钮:
- 绿灯灭,黄灯亮
- 都灭
- 都亮
用逻辑表示
先把两个基本命题用A和B表示:
- 命题\(A\):绿灯亮
- 命题\(B\):黄灯亮
然后需要按按钮的三个情况就是:
- a:\((\lnot A) \land B\)
- b:\((\lnot A) \land (\lnot B)\)
- c:\(A \land B\)
所以要按的情况就是:
\[ ((\lnot A) \land B) \lor ((\lnot A) \land (\lnot B)) \lor (A \land B) \]使用卡诺图

从图中可见,符合的条件可以归纳为:
- A为false
- B为true
用公式表示为:
\[ (\lnot A) \lor B \]所以说:
\[ ((\lnot A) \land B) \lor ((\lnot A) \land (\lnot B)) \lor (A \land B) = (\lnot A) \lor B \]例:三灯游戏
触发条件:
- 绿、黄、红都灭
- 黄灭、红亮
- 绿来、黄亮
- 都亮
用逻辑表示
先把两个基本命题用A和B表示:
- 命题\(A\):绿灯亮
- 命题\(B\):黄灯亮
- 命题\(C\):红灯亮
使用卡诺图
现在有三个命题,所以网络数为:\(2^3=8\)
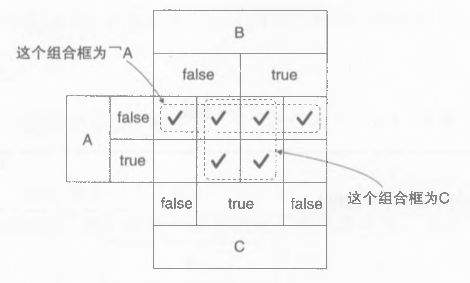
注意B和C的false、true分界是错位的,这样8个网络可以表示所有情况。
- 第一行的四个表示A为false,\(\lnot A\)
- 中间四个组合表示C为true,\(C\)
用公式表示为:
\[ (\lnot A) \lor C \]计算机程序中的未定义
未定义(undefined)情况表示无法取得结果。
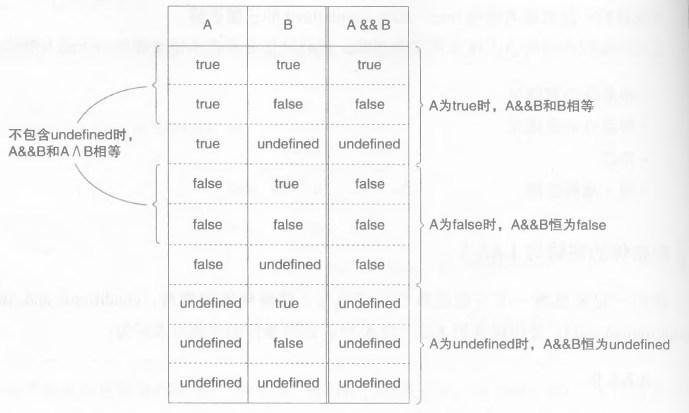
带条件的逻辑与(&&)
带条件的逻辑与(Conditional and, short-circuit logical and),操作符&&。
使用true、false、undefined三种值。
- 不包含undefined的行,和逻辑\(A \land B\)相同。
-
A为true时,
A && B等于B。 -
A为false时,
A && B恒为false。 -
A为undefined时忽略B,不进行任何处理。
A && B恒为undefined。
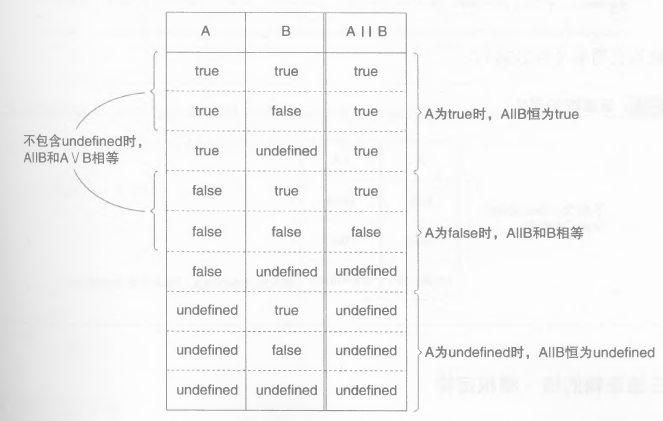
带条件的逻辑或(||)
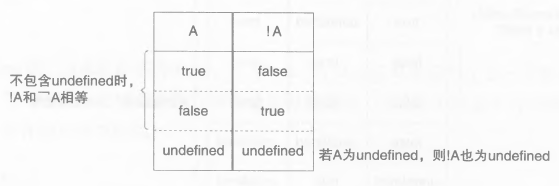
带条件的逻辑非(!)
三值逻辑中的 D Morgan 定理
(!A) || (!B) &= !(A && B) (!A) && (!B) &= !(A || B)

对于程序来说:
if (!(x >= 0 && y >= )) { /* ... */ }
等于:
if (x < 0 || y < 0) { /* ... */ }
小结
对于逻辑工具(逻辑表达式、真值表、文氏图、卡诺图等)的使用,是为了简化复杂逻辑。