从一到无穷大
大数字与无穷大
无穷大的量级
相同量级的无穷大
在无穷大的定义里,部分可能与整体一样大。例如:
奇数与偶数是可以无限一一对应下去的,所以它们是相同量级:
| 奇数 | 1 | 3 | 5 | 7 | 9 | ... |
| 偶数 | 2 | 4 | 6 | 8 | 10 | ... |
反直觉的是,整数与偶数也是可以无限一一对应下去的,所以也是相同量级的:
| 整数 | 1 | 2 | 3 | 4 | 5 | ... |
| 偶数 | 2 | 4 | 6 | 8 | 10 | ... |
普通分数与整数也是可以一一对应的:
- 先列出分子与分母相加后和为2的分数,只有一个:\(\frac{1}{1}\)
- 列出分子与分母相加后和为3的分数,有两个:\(\frac{1}{2}\)、\(\frac{2}{1}\)
- 列出分子与分母相加后和为4的分数,有三个:\(\frac{1}{3}\)、\(\frac{2}{2}\)、\(\frac{3}{1}\)
- 还可以继续列下去……
| 整数 | 1 | 2 | 3 | 4 | 5 | 6 | ... |
| 普通分数 | \(\frac{1}{1}\) | \(\frac{1}{2}\) | \(\frac{2}{1}\) | \(\frac{1}{3}\) | \(\frac{2}{2}\) | \(\frac{3}{1}\) | ... |
不同量级的无穷大
普通分数可以转化为无限循环小数:
- \(\frac{2}{3} = 0.\dot{6}\)
- \(\frac{3}{7} = 0.\dot{4}2857\dot{1}\)
之前说这普通分数可以与整数一一对应,所以循环小数可以与整数一一对变。
但是对于无限不循环小数,例如:
- \(0.2928390182\cdots\)
- \(0.9388273293\cdots\)
- \(0.5318872293\cdots\)
- \(\cdots\)
因为后面可以有无限多个位,随着位数向后有着无限可能性 (无法写完整一个无限不循环小数),所以无法和整数一一对应。
对于两条不同长度的线段AB与AC,它们线段上包含点的数量也是一样多的,可以一一对应的。
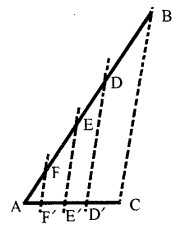
连接BC,把ABC作为一个三角形,可以看到有无数条与底平等的线段如: \(D\)与\(D'\)、\(E\)与\(E'\)、\(F\)与\(F'\)……
如果AB与AC上的每一个点都用从0到1的小数对应每个点在自己所在线段中位置, 也对应了都是相同的小数对小数的集合。
再举一个例子,正方形CDEF上的点的数量与线段AB上点的数量是一样的。 例如取线段上\(0.75120386\dots\)这个点,把这个数字按奇数与偶数分开, 组成两个不同的数\(0.7108\dots\)与\(0.5236\dots\),作为方形水平和垂直方向的点的位置:
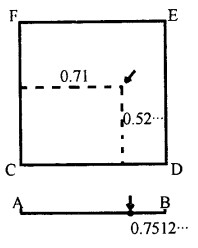
这样所有方形上的点都可以对应到线段上。
同样如果把线段上一个点所代表的小数的数字分成三份,可以把线段上的点和立方体对应。
有没有比线段上点的数量更大的无穷大呢? 有,各种曲线的样式的数量比几何图形中点的数量还要大。 曲线和线段一样有无穷多个点,每个点的弯曲又有无穷多种可能性。
表示无穷大的量级
这样目前我们知道有三个不同量级的无穷大数列。
数学家用希伯莱字母\(\aleph\)(Aleph,阿莱夫)表示无穷大, 再用下标数字表示无穷大的级别,这样包括无穷大在内的数字数列就表示为:
\[ \begin{equation} 1,2,3,4,5,\cdots,\aleph_1,\aleph_2,\aleph_3,\cdots \end{equation} \label{numb2ifnt} \]以后表示数字可以用:
- 一副扑克牌有54张。
- 整数或普通分数的数量都是\(\aleph_0\)个。
- 一条线段上有\(\aleph_1\)个点。
- 曲线的样式有\(\aleph_2\)种。
- 目前还没有想象出来能用\(\aleph_3\)来表示的无穷大数来。
自然数与人工数
数论(这里的数只包含整数)这一大分支没有找到实际性的用途, 是与其科学无关的最纯粹的数学。
反证法
质数是不是有限的?
欧几里得(Euclid)假设有一个最大的质数\(N\),那么把所有质数乘起来,再加上1:
\[ \begin{equation} (1 \times 2 \times 3 \times 5 \times 7 \times 11 \times 13 \times \cdots \times N) + 1 \end{equation} \label{prime-mute-add} \]这个计算的结果肯定比假设的最大质数\(N\)要大,但是不能被任何一个质数(包括\(N\)在内) 除尽,肯定会剩下1。
所以假设不成立,这种证明方法叫作「反证法」。
过筛法找出质数
- 列出所有自然数:\(1,2,3,4,5,\cdots\)
- 从小到大一个一个去掉质数的倍数。如:去掉所有2的倍数,剩下的再去掉3的倍数……
通过这种方法已经得到了10亿以内的质数表。
寻找质数的公式
费马(Pierre Fermat)认为可能通过以下公式找到的必然是质数:
\[ \begin{equation} 2^{2^n} + 1 \end{equation} \label{fermat-prime} \]例如:
\[ \begin{equation} \begin{split} 2^{2^1} + 1 &= 5 \\ 2^{2^2} + 1 &= 17 \\ 2^{2^3} + 1 &= 257 \\ 2^{2^4} + 1 &= 65537 \end{split} \end{equation} \]但欧拉(Leonard Euler)指出到了第五个数不对:
\[ \begin{equation} 2^{2^5} + 1 = 4 294 967 297 = 6 700 417 \times 641 \end{equation} \]另一个公式也能用来寻找质数:
\[ \begin{equation} n^{2} - n + 41 \end{equation} \label{prime-41} \]但是\(n\)只能在1到40范围内有效,到了41就不成立了: \(41^{2} - 41 + 41 = 41^{2}\) 这是一个平方数,不是一个质数。
还有另一个公式:
\[ \begin{equation} n^{2} - 79n + 1601 \end{equation} \label{prime-79} \]这个公式在1到79时成立,但是当n=80时,它又不成立了。
费马大定理
费马在法文版的《算术学》中看到勾股定理后:
\[ \begin{equation} x^{2} + y^{2} = z^{2} \end{equation} \label{gou-gu} \]在书边的空白处写下了笔记:
- \(x^2 + y^2 = z^2\)有无数的整数解。
- \(x^n+y^n=z^n\)这个方程在\(n \gt 2\)时,永远没有整数解。
他后来说:「我当时想出了一个绝妙的证明方法,但是书上的空白太窄了,写不下。」
三百年来数学家证明\(n \lt 269\)时确实没有整数解,但不能保证\(n\)在任何情况下都成立。
虚数
虚数与复数
虚拟把\(\sqrt{-1}\)作为基数,记作\(i\):
\[ \begin{equation} \begin{split} \sqrt{-9} &= \sqrt{9} \times \sqrt{-1} &= 3i \\ \sqrt{-7} &= \sqrt{7} \times \sqrt{-1} &= 0.246\cdots i \end{split} \end{equation} \]实数与虚数还能结合起来表示,这种形式被称为「复数」:
\[ \begin{equation} 5 + \sqrt{-15} = 5 + \sqrt{15} i \end{equation} \]复数的几何意义
复数有实用的几何意义,把横轴代表实数,把纵轴代表虚数, 像是\(3+4i\)这样的复数可以表示为坐标系上的点。
当这个复数乘以虚数单位\(i\)时,相当地几何图形上逆时针转90度:
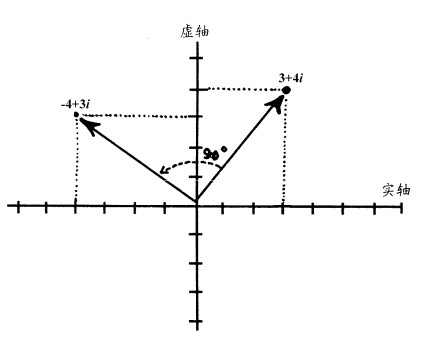
计算过程,因为\(i=\sqrt{-1}\),所以\(i^2 = \sqrt{-1} \times \sqrt{-1} = -1\):
\[ \begin{equation} \begin{split} (3+4i) \times i &= 3i + 4i^2 \\ &= 3i + 4 \times -1 \\ &= 3i - 4 \\ &= -4 + 3i \end{split} \end{equation} \]例子,传说中的藏宝只有文字描述:
- 有一棵橡树\(B\)和一棵松树\(C\),有一个旗杆\(A\)。
- 从旗杆\(A\)出发走到橡树\(B\),记住距离为\(AB\)
- 从橡树右转直角(即顺时针转90度),走出与\(AB\)相同的距离,打个桩\(D\)。
- 回到旗杆\(A\),走到松树\(C\)。记住距离为\(AC\)。
- 在松树的位置左转直角(即逆时针转90度),走出与\(AC\)相同的距离,打个桩\(E\)。
- 宝藏就在\(DE\)连接的中间。
现在有一个问题,橡树\(B\)和松树\(C\)都还在,但是旗杆\(A\)时间年代久远已经不在了。
- \(B\)和\(C\)是已经确定的点,那么我们把坐标系的\((-1,0)\)套到\(B\)上, 把\((1,0)\)套到\(C\)上,那么它们中间正好就是原点。
- \(A\)点在什么地方不确定,可能即不在实轴上也不是虚轴上,
- 所以按复数记为\(A=a+bi\)它的坐标就是\((a,b)\)
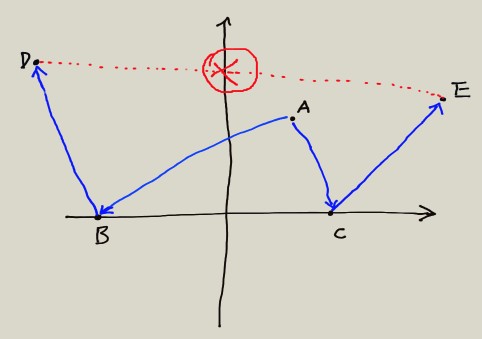
计算出:
- A到B的距离是\(-1-A\)
- A到C的距离是\(1-A\)
把这两个距离分别顺时针和逆时针转90度:
- \((-i)[-1-A] + 1 = i(A+1) + 1\)
- \((+i)[ 1-A] - 1 = i(1-A) - 1\)
宝藏在两个桩的中间,所以把上面两个复数求和减半:
\[ \begin{equation} \begin{split} & \frac{1}{2}[i(A+1) + 1 + i(1-A) - 1] \\ = & \frac{1}{2}[Ai + i + 1 + i - Ai - 1] \\ = & \frac{1}{2}(i + i) = i \end{split} \end{equation} \]最后的结果就是在虚轴上\(i\)的位置,而旗杆\(A\)的位置已经地计算过程中被消除了。
如果还不信,可以自己在纸上画。无论旗杆在什么地方,宝藏永远在\(i\)的位置。