卷积神经网络

卷积神经网络

卷积神经网络的结构

简单郑积神经网络的例子：6x6像素大小的二色位图，表示手写的数字1、2、3三种结果。

卷积层提取样本的特征

「卷积层」（Convolution Layer），「池化层」（）

卷积神经网络不是用和位图上每个像素一一对应的方式来输入图片的，而是用称为 「卷积核」的固定模式特征来遍历图片。通常使用5x5大小的特征，这里为了简单我们用3x3 的大小。

在这里我们选择一个3x3斜线/（Slash）作为特征，就称为过滤器S（斜线过滤器）：

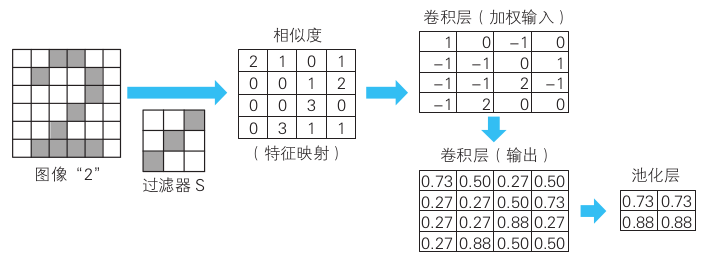
遍历一个数字2的6x6样本，统计重合的像素数量称为「相似度」：

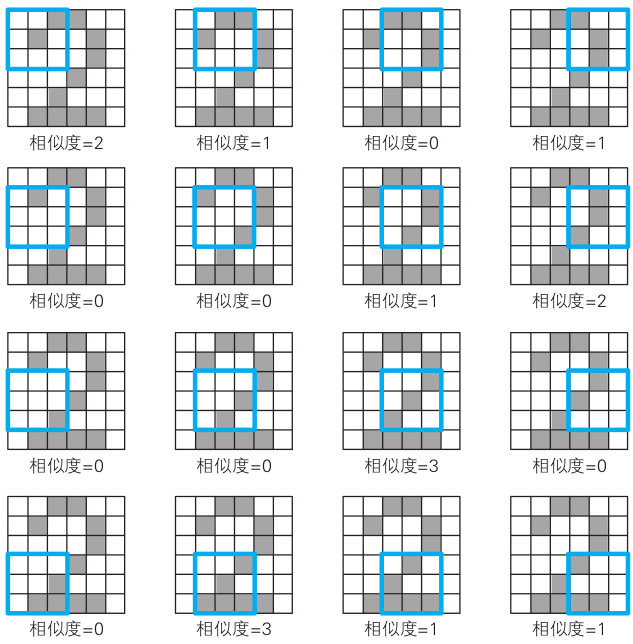
整理成8x8表格就过滤器S得到的卷积（convolution）的结果，称为特征映射（feature map）：

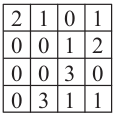
特殊映射的每个元素都要加上偏置\(b\)（这个例子里我们用的是\(-1\)）， 然后映射为新的加权输入：

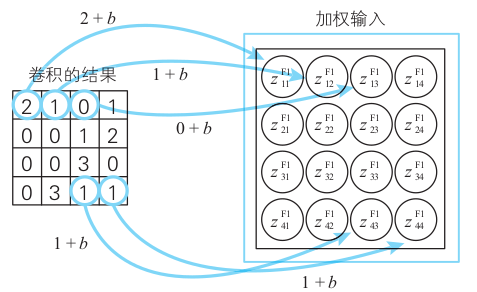
加权输入的每个元素再代入激活函数（这个例子里用的还是Sigmoid函数）， 映射为卷积层神经元的输出：

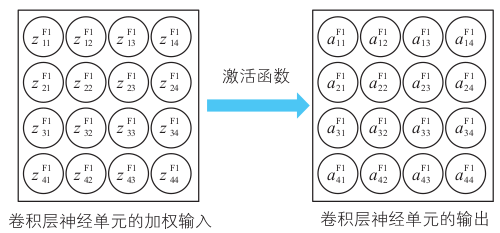
池化层对信息进行压缩

这里为了简单使用的压缩方法是「最大池化」（max pooling）。8x8的卷积层输出分成 4个不重叠的2x2区域(通常选择2x2但也可以用别的大小)，每个区域找一个最大值：

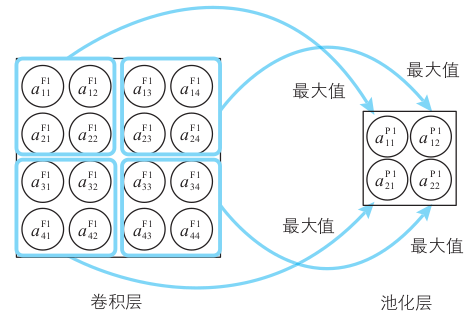
常用的池化法有：

• 最大池化：取最大值。
• 平均池化：取平均值。
• L2池化：对于\(n\)个输出\(a_1, a_2, \cdots , a_n\)，取：\(\sqrt{a_1 + a_2 + \cdots + a_n}\)

正确识别

适当的「过滤器」和「偏置」可以让网络识别出正确的结果。例如上面的例子里数字\(2\) 的池化结果要大于\(1\)和\(3\)：

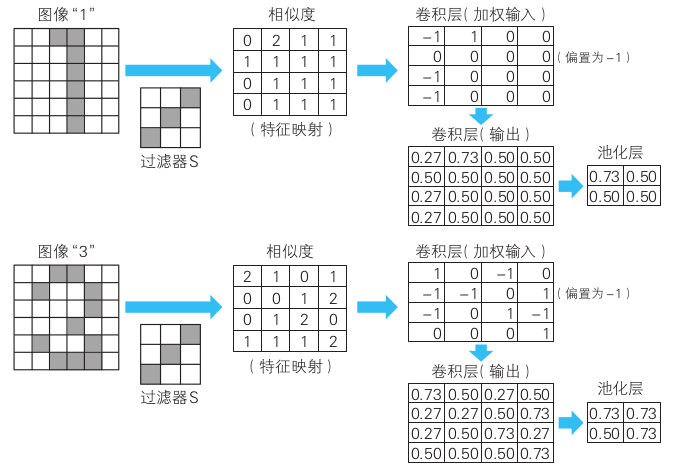
卷积神经网络的变量关系式

输入层

对应图像像素的\(i\)行\(j\)列的值：

\[ \begin{equation} x_{i,j} \end{equation} \label{cnnm01} \]

用\(a^{\rm I}\)表示输入，则有：

\[ \begin{equation} a^{{\rm I}k}_{i,j} = x_{i,j} \end{equation} \label{cnnm02} \]

过滤器

用\(w^{\rm F}\)表示第\(k\)个特征映射的过滤器的\(i\)行\(j\)列。通常采用5x5，但这个例子里用3x3：

\[ \begin{equation} w^{{\rm F}k}_{i,j} \end{equation} \label{cnnm03} \]

卷积层

\(w^{\rm F}\)表示过滤器\(k\)的\(i\)行\(j\)列的神经元的的权重 ：

\[ \begin{equation} w^{{\rm F}k} \end{equation} \label{cnnm04} \]

卷积值用\(c^{\rm F}\)表示，以3x3特征为例，设卷积开始的位置为\(i,j\)：

\[ \begin{equation} c^{{\rm F}k}_{i,j} = w^{{\rm F}k}_{1,1} \cdot x_{i,j} + w^{{\rm F}k}_{1,2} \cdot x_{i,j+1} + w^{{\rm F}k}_{1,3} \cdot x_{i,j+2} + \cdots + w^{{\rm F}k}_{3,3} \cdot x_{i+2,j+2} \end{equation} \label{cnnm05} \]

\(b^{\rm F}\)表示卷积层第\(k\)个子层的\(i\)行\(j\)列的神经元的的偏置， 因为各个特殊映射中是偏置都是相同的，所以不用注明下标：

\[ \begin{equation} b^{{\rm F}k} \end{equation} \label{cnnm06} \]

\(z^{\rm F}\)表示卷积层第\(k\)个子层的\(i\)行\(j\)列的神经元的加权输入：

\[ \begin{equation} z^{{\rm F}k}_{i,j}= w^{{\rm F}k}_{1,1} \cdot x_{i,j} + w^{{\rm F}k}_{1,2} \cdot x_{i,j+1} + w^{{\rm F}k}_{1,3} \cdot x_{i,j+2} + \cdots + w^{{\rm F}k}_{3,3} \cdot x_{i+2,j+2} + b^{{\rm F}k} \end{equation} \label{cnnm07} \]

\(a^{\rm F}\)表示卷积层第\(k\)个子层的\(i\)行\(j\)列的神经元的输出：

\[ \begin{equation} a^{{\rm F}k}_{i,j}=a(z^{{\rm F}k}_{i,j}) \end{equation} \label{cnnm08} \]

池化层

\(z^{\rm P}\)表示池化层第\(k\)个子层的\(i\)行\(j\)列的神经元的输入，通常是前一层的输出：

\[ \begin{equation} z^{{\rm P}k}_{i,j} = max( a^{{\rm F}k}_{2i-1,2j-1}, a^{{\rm F}k}_{2i-1,2j}, a^{{\rm F}k}_{2i,2j-1}, a^{{\rm F}k}_{2i,2j}) \end{equation} \label{cnnm09} \]

\(a^{\rm P}\)表示池化层第\(k\)个子层的\(i\)行\(j\)列的神经元的输出，与输入值\(z^P\)一致：

\[ \begin{equation} a^{{\rm P}k}_{i,j} = z^{{\rm P}k}_{i,j} \end{equation} \label{cnnm10} \]

输出层

\(w^{\rm O}\)表示从池化层第\(k\)个子层的\(i\)行\(j\)列的神经元指向输了层的第\(n\) 个神经单元的箭头的权重：

\[ \begin{equation} w^{{\rm O}n}_{k-i,j} \end{equation} \label{cnnm11} \]

\(b^{\rm O}\)表示输出层第\(n\)个神经元的的偏置：

\[ \begin{equation} b^{\rm O}_n \end{equation} \label{cnnm12} \]

\(z^{\rm O}\)表示输出层第\(n\)个神经元的加权输入，以输出层有3个神经元为例：

\[ \begin{equation} \begin{split} z^{\rm O}_n = & + w^{{\rm O}n}_{1,1,1}a^{{\rm p}1}_{1,1} + w^{{\rm O}n}_{1,1,2}a^{{\rm p}1}_{1,2} + \cdots \\ & + w^{{\rm O}n}_{2,1,1}a^{{\rm p}2}_{1,1} + w^{{\rm O}n}_{2,1,2}a^{{\rm p}2}_{1,2} + \cdots \\ & + w^{{\rm O}n}_{3,1,1}a^{{\rm p}3}_{1,1} + w^{{\rm O}n}_{3,1,2}a^{{\rm p}3}_{1,2} + \cdots \\ & + b^{\rm O}_n \end{split} \end{equation} \label{cnnm13} \]

\(a^{\rm O}\)表示输出层第\(n\)个神经元的输出：

\[ \begin{equation} a^{\rm O}_n = a(z^O_n) \end{equation} \label{cnnm14} \]

样本的正解

\(t_n\)表示输出层第\(n\)个神经元的的正解：

\[ \begin{equation} t_n \end{equation} \label{cnnm15} \]

例如：

• 正解为\(1\)时，\(t_1=1, t_2=0, t_3=0\)
• 正解为\(2\)时，\(t_1=0, t_2=1, t_3=0\)
• 正解为\(3\)时，\(t_1=0, t_2=0, t_3=1\)

第\(k\)个样本的平方误差\(C_k\)：

\[ \begin{equation} C = \frac{1}{2} { (t_1[k] - a^O_1[k])^2 + (t_2[k] - a^O_2[k])^2 + \cdots + (t_j[k] - a^O_j[k])^2 } \end{equation} \label{cnnm16} \]

代价函数\(C_{\rm T}\)：

\[ \begin{equation} C_{\rm T} = C_1 + C_2 + \cdots + C_n \end{equation} \label{cnnm17} \]

概览

卷积神经网络的误差反向传播法

• 卷积层一共有\(K\)层，用变量\(k\)表示其中第几层
• 过滤器大小为\(I \times J\)，用\(i,j\)表示坐标
• 输出层一共有\(N\)个神经元，用变量\(n\)表示其中第几个

梯度

\[ \begin{equation} \begin{split} (& \Delta w^{{\rm F}1}_{1,1} &, \cdots , & \Delta w^{{\rm F}1}_{i,j} &, \cdots , & \Delta w^{{\rm F}1}_{I,J} &, \Delta b^{{\rm F}1}, & \cdots \\ & \Delta w^{{\rm F}k}_{1,1} &, \cdots , & \Delta w^{{\rm F}k}_{i,j} &, \cdots , & \Delta w^{{\rm F}k}_{I,J} &, \Delta b^{{\rm F}k}, & \cdots \\ & \Delta w^{{\rm F}K}_{1,1} &, \cdots , & \Delta w^{{\rm F}K}_{i,j} &, \cdots , & \Delta w^{{\rm F}K}_{I,J} &, \Delta b^{{\rm F}K}, & \cdots \\ & \quad & & & & & & \\ & \Delta w^{{\rm O}1}_{1-1,1} &, \cdots , & \Delta w^{{\rm O}1}_{1-i,j} &, \cdots , & \Delta w^{{\rm O}1}_{1-I,J} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \Delta w^{{\rm O}1}_{k-1,1} &, \cdots , & \Delta w^{{\rm O}1}_{k-i,j} &, \cdots , & \Delta w^{{\rm O}1}_{k-I,J} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \Delta w^{{\rm O}1}_{K-1,1} &, \cdots , & \Delta w^{{\rm O}1}_{K-i,j} &, \cdots , & \Delta w^{{\rm O}1}_{K-I,J} &, \Delta b^{\rm O}_1, & \cdots \\ & \quad & & & & & & \\ & \Delta w^{{\rm O}n}_{1-1,1} &, \cdots , & \Delta w^{{\rm O}n}_{1-i,j} &, \cdots , & \Delta w^{{\rm O}n}_{1-I,J} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \Delta w^{{\rm O}n}_{k-1,1} &, \cdots , & \Delta w^{{\rm O}n}_{k-i,j} &, \cdots , & \Delta w^{{\rm O}n}_{k-I,J} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \Delta w^{{\rm O}n}_{K-1,1} &, \cdots , & \Delta w^{{\rm O}n}_{K-i,j} &, \cdots , & \Delta w^{{\rm O}n}_{K-I,J} &, \Delta b^{\rm O}_n, & \cdots \\ & \quad & & & & & & \\ & \Delta w^{{\rm O}N}_{1-1,1} &, \cdots , & \Delta w^{{\rm O}N}_{1-i,j} &, \cdots , & \Delta w^{{\rm O}N}_{1-I,J} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \Delta w^{{\rm O}N}_{k-1,1} &, \cdots , & \Delta w^{{\rm O}N}_{k-i,j} &, \cdots , & \Delta w^{{\rm O}N}_{k-I,J} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \Delta w^{{\rm O}N}_{K-1,1} &, \cdots , & \Delta w^{{\rm O}N}_{K-i,j} &, \cdots , & \Delta w^{{\rm O}N}_{K-I,J} &, \Delta b^{\rm O}_N) & \\ = - \eta \Bigg( & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}1}_{1,1} } &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}1}_{i,j} } &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}1}_{I,J} } &, \frac{\partial C_{\rm T}}{\partial b^{{\rm F}1}}, & \cdots \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}k}_{1,1} } &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}k}_{i,j} } &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}k}_{I,J} } &, \frac{\partial C_{\rm T}}{\partial b^{{\rm F}k}}, & \cdots \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}K}_{1,1} } &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}K}_{i,j} } &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm F}K}_{I,J} } &, \frac{\partial C_{\rm T}}{\partial b^{{\rm F}K}}, & \cdots \\ & \quad & & & & & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{1-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{1-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{1-I,J}} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{k-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{k-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{k-I,J}} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{K-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{K-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}1}_{K-I,J}} &, \frac{\partial C_{\rm T}}{\partial b^{\rm O}_1}, & \cdots \\ & \quad & & & & & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{1-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{1-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{1-I,J}} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{k-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{k-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{k-I,J}} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{K-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{K-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}n}_{K-I,J}} &, \frac{\partial C_{\rm T}}{\partial b^{\rm O}_n}, & \cdots \\ & \quad & & & & & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{1-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{1-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{1-I,J}} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{k-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{k-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{k-I,J}} &, & \\ & \vdots & \vdots & \vdots & \vdots & \vdots & & \\ & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{K-1,1}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{K-i,j}} &, \cdots , & \frac{\partial C_{\rm T}}{\partial w^{{\rm O}N}_{K-I,J}} &, \frac{\partial C_{\rm T}}{\partial b^{\rm O}_N} & \Bigg) \\ \end{split} \end{equation} \label{cnngd01} \]

分量的总数量：

\[ (3 \times 3 + 1) \times 3 + (2 \times 2 \times 3 + 1) \times 3 = 96 \]

96个分量至少需要96个样本：

\[ C_{\rm T} = C_{\rm 1} + C_{\rm 2} + \cdots + C_{\rm 96} \]

「」