神经网络数学基础

数学基础

函数

一次函数

一元一次函数：

\[ \begin{equation} y = ax + b \quad \{a \neq 0\} \end{equation} \label{fc_yc11} \]

• \(a\)、\(b\)为常数。
• \(a\)为「斜率」（slope）。
• \(b\)为「截距」。

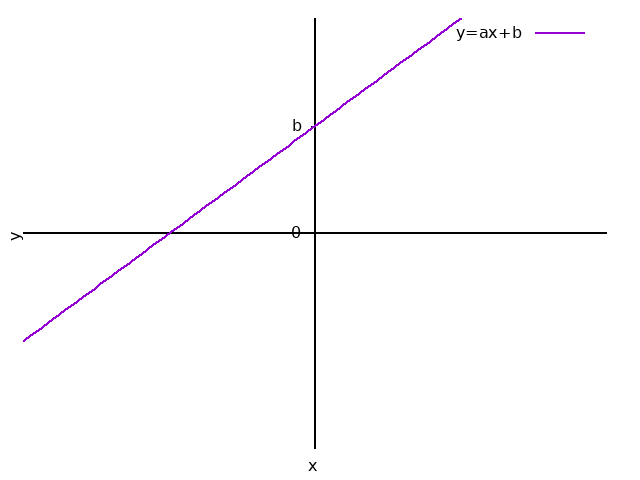
二元一次函数：

\[ \begin{equation} y = ax_1 + bx_2 + c \quad \{a \neq 0, b \neq 0\} \end{equation} \label{fc_yc21} \]

三元一次函数：

\[ \begin{equation} y = ax_1 + bx_2 + cx_3 + d \quad \{a \neq 0, b \neq 0, c \neq 0\} \end{equation} \label{fc_yc31} \]

一次函数正好对照到神经网络的输入：

\[ \begin{equation} z = w_1x_1 + w_2x_2 + w_3x_3 + b \end{equation} \]

二次函数

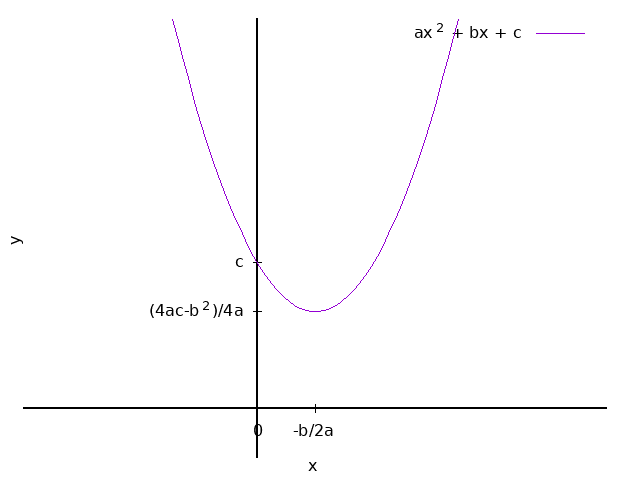
一元二次函数：

\[ \begin{equation} y = ax^2 + bx + c \quad \{c \neq 0\} \end{equation} \label{fc_yc12} \]

• \(a\)、\(b\)、\(c\)为常数。

\[ \begin{equation} y = ax_1^2 + bx_1x_2 + cx_2^2 + px_1 + qx_2 + r \quad \{a \neq 0,c \neq 0\} \end{equation} \label{fc_yc22} \]

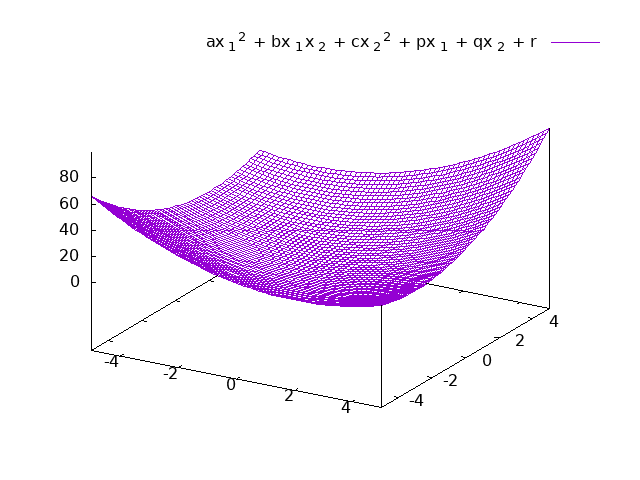
• \(a\)、\(b\)、\(c\)、\(p\)、\(q\)、\(r\)为常数。

单位阶跃函数

\[ \label{fc_jl} u(x)=\begin{cases} \begin{equation} \begin{split} & 0 \quad \quad \quad & \{ x \lt 0 \} \\ & 1 \quad \quad \quad & \{ x \geq 0 \} \end{split} \end{equation} \end{cases} \]

单位阶跃函数在\(x = 0\)处不连接，也就是在原点不可导。 因为不可导，所以不作为主要的激活函数。

指数函数

\[ \begin{equation} y = a^x \quad \quad \{ x \gt 0 , x \neq 1 \} \end{equation} \label{fc_pw} \]

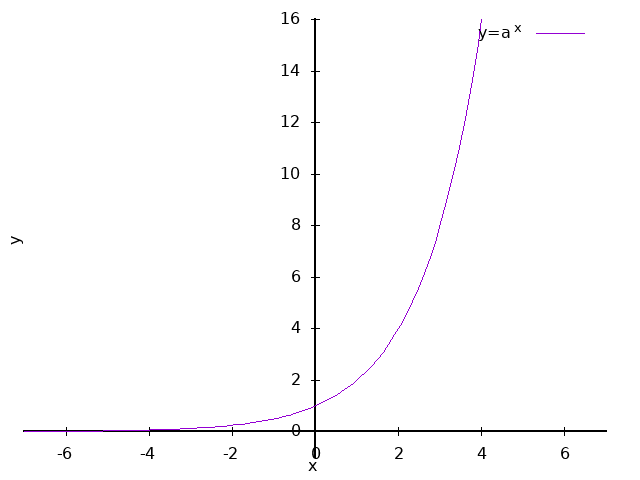
Sigmoid函数

\[ \begin{equation} \sigma(x) = \frac{1}{1 + {\rm e}^{-x}} = \frac{1}{1+{\rm exp}(-x)} \quad \quad ({\rm e}=2.71828 \cdots) \end{equation} \label{fc_sgmd} \]

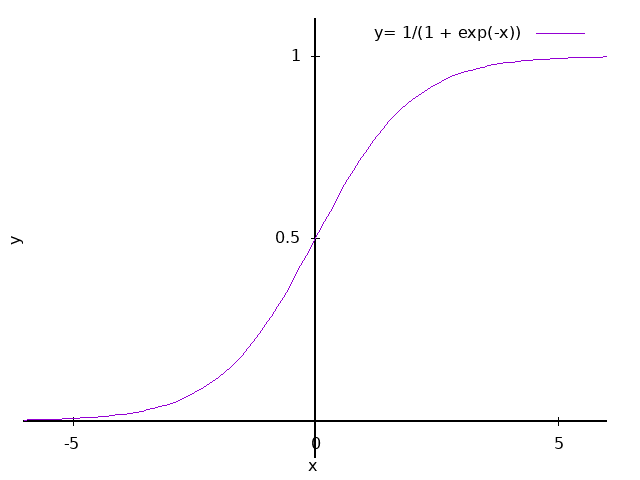
正态分布与概率密度函数

在设定神经网络时，要确定权重和偏置的初始值。这时候「正态分布」（normal distribution） 是一个有用的工具。

态分布也被称为高斯分布。它是以天才卡尔·弗里德里希·高斯（Carl Friedrich Gauss） 的名字命名的。

如果对概率分布作图，得到一条倒钟形曲线，样本的平均值、众数以及中位数是相等的， 那么该变量就是正态分布的。

正态分布是符合以下「概率密度函数」\(f(x)\)的概率分布：

\[ \begin{equation} f(x) = \frac{1}{\sqrt{2\pi}\sigma}{\rm e}^{-\frac{(x- \mu)^2} {2\sigma^2}} \end{equation} \label{fc_pcd} \]

• \(\mu\)代表「期望值」，就是所有样本的平均值。
• \(\sigma\)代表「标准差」，与Sigmoid函数中的没有关系 ，是数据集与相配平均值的偏离程度。

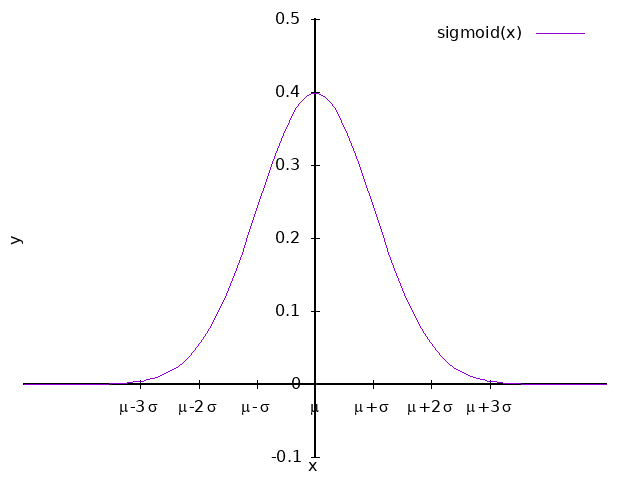
从上图中可以看到非常著名的\(3|Theta\)原则：

• 约有 68.2% 的点落在±1个标准差的范围内\([\mu - \sigma, \mu + \sigma]\)
• 约有 95.5% 的点落在±2个标准差的范围内\([\mu - 2\sigma, \mu + 2\sigma]\)
• 约有 99.7% 的点落在±3个标准差的范围内\([\mu - 3\sigma, \mu + 3\sigma]\)。

当\(\mu=0, \sigma = 1\)时，正态分布就成为「标准正态分布」：

\[ \begin{equation} f(x) = \frac{1}{\sqrt{2\pi}} {\rm e}^{(-\frac{x^2}{2})} \end{equation} \label{fc_sdpcd} \]

如果随机数是按正态分布生成的，被称为「正态分布随机数」。

例如，Excel中生成正态公布随机数的公式为：NORM.INV(RAND(), mu, sgm)。 mu代表期望值，sgm代表标准差。

数列

数列的表示

数列中每一个成员称为「项」。例如有一个数列被命名为\(a\)：

• 表示其中的第\(n\)项时，记为：\(a_n\)
• 表示整个数列时用符合符号，记为：\(\{a_n\}\)

神经网络中用类似数列项的记法表示神经元的位置：

• 层数用上标表示
• 位数用下表表示

例录第\(l\)层的第\(j\)个神经元记为：

\[ \begin{equation} a^l_j \end{equation} \label{nq_nu} \]

通项式与递推关系

「通项公式」是数列中元素的项数\(n\)与元素值关系的表达式。例如偶数列的通项公式为： \(a_n=2n\)

「递归定义」是通过相邻项的关系来表示数列。

一般如果知道首项\(a_1\)和任意相邻\(a_n\)、\(a_{n-1}\)的关系，就可以确定这个数列， 这个关系式称为「递推关系式」。

例，首项\(a_1=1\)，关系式\(a_{n+1}=a_n+2\)，则：

\[ \begin{split} a_1 &= 1 \\ a_2 &= a_{1+1} &= a_1 + 2 &= 1 + 2 &= 3 \\ a_3 &= a_{2+1} &= a_2 + 2 &= 3 + 2 &= 5 \\ a_4 &= a_{3+1} &= a_3 + 2 &= 5 + 2 &= 7 \\ \vdots \end{split} \]

例，首项\(c_1=3\)，关系式\(c_{n+1}=2c_n\)，则：

\[ \begin{split} c_1 &= 3 \\ c_2 &= c_{1+1} &= 2 \times c_1 &= 2 \times 3 &= 6 \\ c_3 &= c_{2+1} &= 2 \times c_2 &= 2 \times 6 &= 12 \\ c_4 &= c_{3+1} &= 2 \times c_3 &= 2 \times 12 &= 24 \\ \vdots \end{split} \]

递推关系式的优点是更方便计算机运算，比如对于阶乘：

\[ n!=1 \times 2 \times 3 \times \cdots \times n \]

计算机的计算方式是：

\[ \begin{split} a_1 = 1 \quad , \quad a_{n+1} = (n+1)a_n \end{split} \]

联立递推关系式

设\(a_1=b_1=1\)，根据以下递推关系：

\[ \begin{cases} \begin{split} a_{n+1} &= a_n + 2b_n + 2 \\ b_{n+1} &= 2a_n + 3b_n + 1 \end{split} \end{cases} \]

可以推导出\(a_n\)、\(b_n\)：

\[ \begin{cases} \begin{split} a_2 & = a_1 + 2b_1 + 2 &= & 1 + 2 \times 1 + 2 &= 5 \\ b_2 & = 2a_1 + 3b_1 + 1 &= & 2 \times 1 + 3 \times 1 + 1 &= 6 \end{split} \end{cases} \] \[ \begin{cases} \begin{split} a_3 &= a_2 + 2b_2 + 2 &= & 5 + 2 \times 6 + 2 &= 19 \\ b_3 &= 2a_2 + 3b_2 + 1 &= & 2 \times 5 + 3 \times 6 + 1 &= 29 \end{split} \end{cases} \]

这种把多个数列的递推式联合起来组成一组的，称为「联立递推关系式」。

神经网络中可以把所有神经单元的输入输出在数学上视为用联立递推式联系起来的。

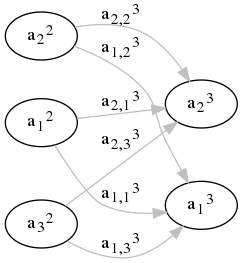
设\(a(z)\)为激活函数，\(b^3_1\)和\(b^3_2\)为偏置，可以得到：

\[ \begin{cases} \begin{split} a^3_1 &= a(w^3_{1,1} a^2_1 + w^3_{1,2} a^2_2 + w^3_{1,3} a^2_3 + b^3_1) \\ a^3_2 &= a(w^3_{2,1} a^2_1 + w^3_{2,2} a^2_2 + w^3_{2,3} a^2_3 + b^3_1) \end{split} \end{cases} \]

可以看出，第三层的输出结果\(a^3_1\)、\(a^3_2\)是由上一层的输出结果 \(a^2_1\)、\(a^2_2\)、\(a^2_3\)决定的。

神经网络中的「反向误差法」中用到了这种递推关系。

数列求和

数学上用符号\(\Sigma\)（Sigma）表示对数列求和。例如对于数列\(\{a_n\}\)：

\[ \begin{equation} \sum_{k=1}^n a_k = a_1 + a_2 + a_3 + \cdots + a_{n-1} + a_n \end{equation} \label{nq_sgm} \]

\(k=1\)中的\(k\)类似于计算机程序循环结构中定义的步进变量， 一般也用\(i\)、\(j\)、\(k\)、\(l\)、\(m\)、\(n\)来命名：

\[ \begin{split} \sum_{n=1}^5 a_n &= a_1 + a_2 + a_3 + a_4 + a_5 \\ \sum_{k=1}^7 k^2 &= 1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2 + 7^2 \\ \sum_{i=1}^m 2^i &= 2^1 + 2^2 + 2^3 + 2^{m-1} + 2^m \end{split} \]

数列求和的基本性质

\[ \begin{equation} \sum_{k=1}^n(a_k + b_k) = \sum_{k=1}^n a_k + \sum_{k=1}^n b_k \end{equation} \label{nq_sgmsc} \] \[ \begin{equation} \sum_{k=1}^n c a_k = c \times \sum_{k=1}^n a_k \quad \quad c\text{为常量} \end{equation} \label{nq_sgmmc} \]

结合起来：

\[ \begin{equation} \sum_{k=1}^n (k^2-3k+2) = \sum_{k=1}^n k^2 -3\sum_{k=1}^n k +\sum_{k=1}^n 2 \end{equation} \label{nq_sgcp} \]

向量

向量是具有方向与大小的量。以\(A\)为起点，\(B\)为终点的有向线段：

• 起点\(A\)的位置。
• 指向\(B\)的方向。
• 长度\(AB\)。

有向线段\(AB\)所代表的向量用\(\overrightarrow{AB}\)表示， 也可以用\(\overrightarrow{a}\)或不带箭头的黑斜体字母\(a\)表示。

将向量的起点置于原点，用终点的坐标表示向量的方法称为「坐标表示法」：

\[ \begin{equation} a = (x, y) \end{equation} \label{vct_ax} \]

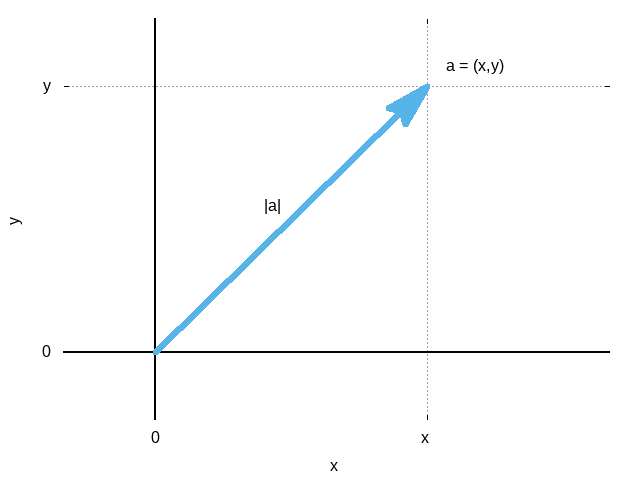
向量的大小

向量的大小用\(|a|\)表示：

\[ \begin{equation} |a| = \sqrt{x^2 + y^2} \end{equation} \label{vct_sz} \]

同理三维空间向量的坐标与大小：

\[ \begin{equation} a = (x, y, z) \end{equation} \label{vct_ax3d} \] \[ \begin{equation} |a| = \sqrt{x^2 + y^2 + z^2} \end{equation} \label{vct_sz3d} \]

向量的相加

绿、蓝、红三个向量相加，结果为橙色的新向量：

\[ \begin{equation} \begin{pmatrix} 0 \\ 0 \\ 8 \\ \end{pmatrix} + \begin{pmatrix} 3 \\ 0 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 5 \\ 0 \\ \end{pmatrix} = \begin{pmatrix} 3 \\ 5 \\ 8 \\ \end{pmatrix} \end{equation} \label{vct_add_tree} \]

向量乘常数

向量乘常数，相当于每个方向上的单个维度的拉伸或缩小：

\[ \begin{equation} \begin{pmatrix} 0 \\ 0 \\ 8 \\ \end{pmatrix} + \begin{pmatrix} 3 \\ 0 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 5 \\ 0 \\ \end{pmatrix} = 8 \times \begin{pmatrix} 0 \\ 0 \\ 1 \\ \end{pmatrix} + 3 \times \begin{pmatrix} 1 \\ 0 \\ 0 \\ \end{pmatrix} + 5 \times \begin{pmatrix} 0 \\ 1 \\ 0 \\ \end{pmatrix} \end{equation} \label{vct_add_mut_tree} \]

向量的线性变换

对于某种变换\(T\)，如果多个向量无论在变换之前还是之后相加，如果产生的结果向量都相同， 那么这种变换\(T\)就被称为「线性变换」（Liner Tranformation Definition）。

线性变换定义：

\[ \begin{equation} \begin{split} T(X+Y) &= T(X) + T(X) \\ T(a \cdot X) &= a \cdot T(X) \end{split} \end{equation} \label{vct_lntsf} \]

向量的旋转、镜像翻转、拉伸操作都是线性变换。 我们可以把多个向量相加，然后再旋转、镜像翻转、拉伸； 或者把每个向量分别旋转、镜像翻转、拉伸，然后再相加。 这二者最后生成的结果向量都是相同的。

向量的叉乘

向量的叉乘用乘法符号\(\times\)表示：

\[ \begin{equation} c = a \times b \end{equation} \label{vct_x_pdt} \]

• 向量\(c\)为以原点为起点，方向与\(a\)和\(b\)二者所在的平面垂直的新向量。
• 向量\(c\)的大小为\(a\)和\(b\)二者所构成的平等四边形的面积

向量叉乘不符合交换率，用右手定则：

手臂是第一个向量，弯曲手指是第二个向量，姆指是第三个向量：

叉乘在科学计算与工程学中有很重要的作用。

向量的内积

向量\(a\)与向量\(b\)之间的夹角为\(\theta\)，则它们的内积记为\(a \cdot b\)，定义：

\[ \begin{equation} a \cdot b = |a| \cdot |b| \cdot \cos \theta \end{equation} \label{vct_im} \]

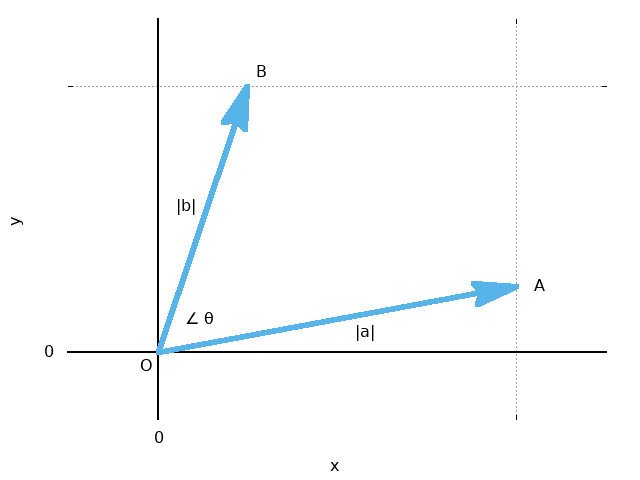
例，如下图\(\overrightarrow{OA} = a\)，\(\overrightarrow{OB} = b\)， \(\overrightarrow{OC} = c\)，\(|a| = |b| = 1\)，\(|c|=\sqrt{2}\)：

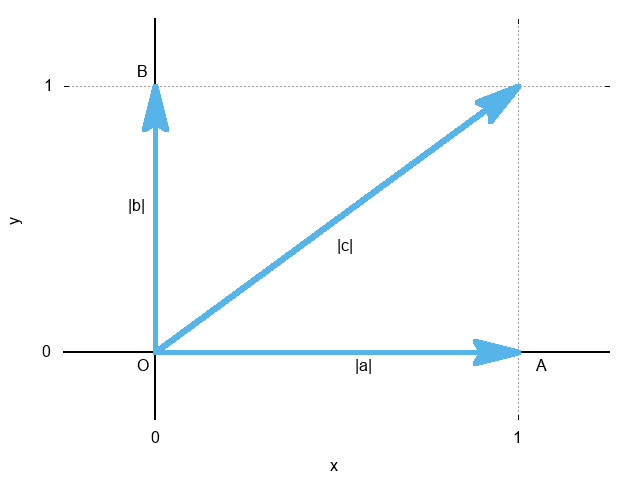
于是有：

\[ \begin{equation} \begin{split} a \cdot a &= |a| \cdot |a| \cdot \cos 0 ^\circ &= 1 \cdot 1 \cdot 1 &= 1 \\ a \cdot b &= |a| \cdot |b| \cdot \cos 90 ^\circ &= 1 \cdot 1 \cdot 0 &= 0 \\ a \cdot c &= |a| \cdot |c| \cdot \cos 45 ^\circ &= 1 \cdot \sqrt{2} \cdot \frac{\sqrt{2}}{2} &= 1 \end{split} \end{equation} \label{vct_imp} \]

向量的内积的几何意义

\[ \begin{equation} a \cdot b = c \end{equation} \label{vct_glm02} \]

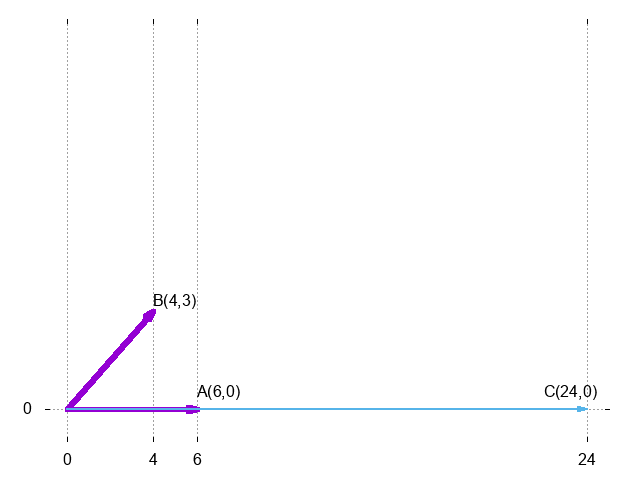
• 向量c起点为原点。
• 向量c的长度为向量\(a\)的长度乘以向量b终点垂直于向量a所在直线的截距离原点的距离。

向量的内积符合交换率，所以无论用哪个向量作为第一个向量结果都一样。

柯西－施瓦茨不等式

\[ \begin{equation} \begin{split} A \cdot B &= |a| \cdot |b| \cdot 1 &= 6 \cdot 5 \cdot 1 &= 30 \\ A \cdot C &= |a| \cdot |c| \cdot \frac{4}{5} &= 6 \cdot 5 \cdot \frac{4}{5} &= 24 \\ A \cdot D &= |a| \cdot |d| \cdot \frac{-4}{5} &= 6 \cdot 5 \cdot \frac{-4}{5} &= -24 \\ A \cdot E &= |a| \cdot |e| \cdot -1 &= 6 \cdot 5 \cdot -1 &= -30 \end{split} \end{equation} \]

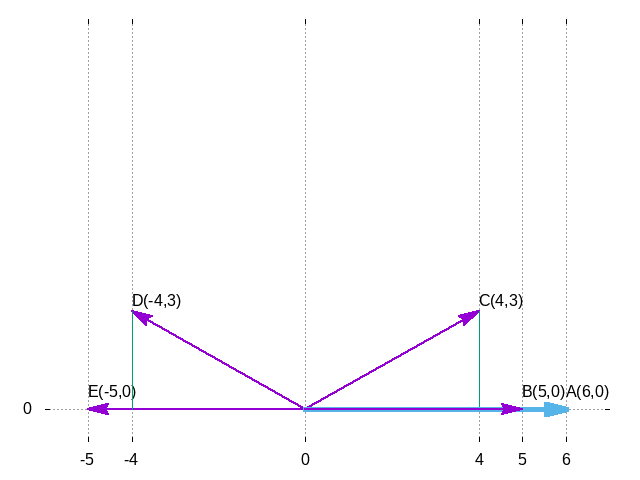
对于任意的\(\theta\)，存在：

\[ -1 \leq \cos \theta \leq 1 \]

每一个部分都乘以\(|a| \cdot |b|\)，得到

\[ -1 \cdot |a| \cdot |b| \leq |a| \cdot |b| \cdot \cos \theta \leq |a| \cdot |b| \cdot 1 \]

这就是「柯西－施瓦茨不等式」：

\[ \begin{equation} - |a| |b| \leq |a| |b| \cos \theta \leq |a| |b| \end{equation} \label{vct_kcswc} \]

根据柯西－施瓦茨不等式可以明白：

• 当两个向量方向相反时（\(\theta = \pi\)时，\(\cos \theta = -1\)），内积值最小。这也是以后梯度下降法的基本原理。
• 当两个向量不平行时（\(0 \lt \theta \lt \frac{\pi}{2}\)时，\( -1 \lt \cos \theta \lt 1\)），内积值在中间。
• 当两个向量方向相同时（\(\theta = 0\)时，\( \cos \theta = 1 \)），内积值最大。

所以内积表示两个向量在多大程序上指向相同的方向，这在「卷积神经网络」 中是一个十分重要的指标。

内积的坐标表示法

当\(a=(a_1,a_2)\)，\(b=(b_1,b_2)\)时：

\[ \begin{equation} a \cdot b = a_1b_1 + a_2b_2 \end{equation} \label{vct_imcdx} \]

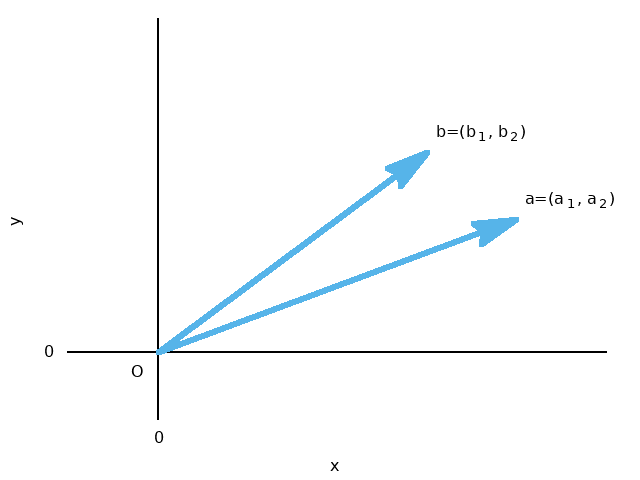
例，当\(a=(2,3)\)， \(b=(5,1)\)时：

\[ \begin{equation} \begin{split} a \cdot b &= 2 \times 5 + 3 \times 1 &= 13 \\ a \cdot a &= 2 \times 2 + 3 \times 3 &= 13 \\ b \cdot b &= 5 \times 5 + 1 \times 1 &= 26 \end{split} \end{equation} \]

同理，三维空间中\(a=(a_1,a_2,a_3)\)，\(b=(b_1,b_2,b_3)\)时：

\[ \begin{equation} a \cdot b = a_1b_1 + a_2b_2 + a_3b_3 \end{equation} \label{vct_im3dcdx} \]

向量的一般化

向量的基本性质可以应用过多维的空间：

• 坐标表示法：\(a=(a_1, a_2, \cdots , a_n)\)
• 内积的坐标表示：\(a\cdot b = a_1b_1+a_2b_2+ \cdot + a_nb_n\)
• 柯西－施瓦茨不等式：\(-|a||b| \leq a\cdot b \leq |a||b|\)

多维向量的性质可以应用到神经网络的神经元输入计算场景中：

\[ z = w_1x_1 + w_2x_2 + w_3x_3 + \cdots + w_nx_n + b \]

转换为内积：

\[ \begin{equation} \begin{cases} \begin{split} w &=(w_1, w_2, \cdots , w_n) \\ x &=(x_1, x_2, \cdots , x_n) \\ z &= w \cdot x + b \end{split} \end{cases} \end{equation} \label{scvt_dowt} \]

张量

「张量」（tensor）是向量概念的扩展，来源于物理应用中的「张力」（tension）。

向固体施加张力时，会在固体截面产生力的作用，即「应力」。应力在不同的截面上 大小和方向各不相同。

「法向量」是垂直于面的向量，法向量的方向不同，应用的方向和大小也不相同。 当法向量为\(x\)、\(y\)、\(z\)轴时，作用在面上的力依次用向量表示为：

\[ \begin{pmatrix} \tau_{11} \\ \tau_{21} \\ \tau_{31} \\ \end{pmatrix} , \begin{pmatrix} \tau_{12} \\ \tau_{22} \\ \tau_{32} \\ \end{pmatrix} , \begin{pmatrix} \tau_{13} \\ \tau_{23} \\ \tau_{33} \\ \end{pmatrix} \]

可以结合为：

\[ \begin{pmatrix} \tau_{11} & \tau_{12} & \tau_{13} \\ \tau_{21} & \tau_{22} & \tau_{23} \\ \tau_{31} & \tau_{32} & \tau_{33} \\ \end{pmatrix} \]

这个张量称为「应力张量」。

矩阵

矩阵的定义

横向为行，纵向为列。\(m\)行\(n\)列的矩阵\(A\)如下图所示：

\[ \begin{equation} A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots & a_{mn} \\ \end{pmatrix} \end{equation} \label{mtx_nml} \]

位于第\(i\)行第\(j\)列的元素用\(aij\)表示。

单列矩阵\(X\)称为「行向量」，单行矩阵\(Y\)你为「列向量」。也可以简称为「向量」：

\[ X = \begin{pmatrix} 3 \\ 1 \\ 2 \\ \end{pmatrix} , Y = \begin{pmatrix} 1 & 5 & 9 \end{pmatrix} \]

行数与列数相同的矩阵，称为「方阵」：

\[ A = \begin{pmatrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \\ \end{pmatrix} \]

对角线\(a_{ii}\)为\(1\)，其他元素为\(0\)的方阵称为「单位矩阵」，用数字1的德语Ein首字母 \(E\)表示。例如2x2的单位矩阵称为二阶单位矩阵，3x3的就是三阶单位矩阵：

\[ E = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix} , E = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \]

矩阵的操作

\[ A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1j} \\ a_{21} & a_{22} & \cdots & a_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{ij} \\ \end{pmatrix} , B = \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1j} \\ b_{21} & b_{22} & \cdots & b_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ b_{i1} & b_{i2} & \cdots & b_{ij} \\ \end{pmatrix} \]

矩阵相等：两个矩阵\(A\)与\(B\)中个对应的元素相等，则\(A=B\)

\[ \begin{equation} \forall a_{ij} = b_{ij} \Rightarrow A=B \end{equation} \label{itx_iope} \]

矩阵和与差：相同位置元素相加相减：

\[ \begin{equation} A + B = \begin{pmatrix} a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1j} + b_{1j} \\ a_{21} + b_{21} & a_{22} + b_{22} & \cdots & a_{2j} + b_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} + b_{i1} & a_{i2} + b_{i2} & \cdots & a_{ij} + b_{ij} \\ \end{pmatrix} \end{equation} \label{itx_iop2} \] \[ \begin{equation} A - B = \begin{pmatrix} a_{11} - b_{11} & a_{12} - b_{12} & \cdots & a_{1j} - b_{1j} \\ a_{21} - b_{21} & a_{22} - b_{22} & \cdots & a_{2j} - b_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} - b_{i1} & a_{i2} - b_{i2} & \cdots & a_{ij} - b_{ij} \\ \end{pmatrix} \end{equation} \label{itx_iop3} \]

矩阵常数倍数：每个元素乘以常数倍数：

\[ \begin{equation} c \times A = c \times \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1j} \\ a_{21} & a_{22} & \cdots & a_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{ij} \\ \end{pmatrix} = \begin{pmatrix} c \times a_{11} & c \times a_{12} & \cdots & c \times a_{1j} \\ c \times a_{21} & c \times a_{22} & \cdots & c \times a_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ c \times a_{i1} & c \times a_{i2} & \cdots & c \times a_{ij} \\ \end{pmatrix} \end{equation} \label{itx_iop5} \]

矩阵的乘积：把\(A\)的\(i\)行与\(B\)的\(j\)列内积，作为\(A \times B\)的\(ij\)：

\[ \begin{equation} C = A \times B = \\ \begin{pmatrix} a_{11} b_{11} + a_{12} b_{21} + \cdots + a_{1j} b_{i1} & a_{11} b_{12} + a_{12} b_{22} + \cdots + a_{1j} b_{i2} & \cdots & a_{11} b_{1j} + a_{12} b_{2j} + \cdots + a_{1j} b_{ij} \\ a_{21} b_{11} + a_{22} b_{21} + \cdots + a_{2j} b_{i1} & a_{21} b_{12} + a_{22} b_{22} + \cdots + a_{2j} b_{i2} & \cdots & a_{21} b_{1j} + a_{22} b_{2j} + \cdots + a_{2j} b_{ij} \\ a_{31} b_{11} + a_{32} b_{21} + \cdots + a_{3j} b_{i1} & a_{31} b_{12} + a_{32} b_{22} + \cdots + a_{3j} b_{i2} & \cdots & a_{31} b_{1j} + a_{32} b_{2j} + \cdots + a_{3j} b_{ij} \\ a_{i1} b_{11} + a_{i2} b_{21} + \cdots + a_{ij} b_{i1} & a_{i1} b_{12} + a_{i2} b_{22} + \cdots + a_{ij} b_{i2} & \cdots & a_{i1} b_{1j} + a_{i2} b_{2j} + \cdots + a_{ij} b_{ij} \\ \end{pmatrix} \end{equation} \label{itx_iop6} \]

• 当矩阵\(A\)的列数等于矩阵\(B\)的行数时，\(A\)与\(B\)可以相乘。
• 矩阵\(C\)的行数等于矩阵\(A\)的行数，\(C\)的列数等于\(B\)的列数。

矩阵乘法一般不满足交换律，除了特殊情况，以下等式是成立的：

\[ \begin{equation} A \times B \neq B \times A \end{equation} \label{itx_iopn7} \]

单位矩阵\(E\)与任意矩阵满足交换律：

\[ \begin{equation} A \times E = E \times A = A \end{equation} \label{itx_iopn7e} \]

乘法结合律：

\[ \begin{equation} (A \times B) \times C = A \times (B \times C) \end{equation} \label{itx_iop7} \]

乘法左分配律：

\[ \begin{equation} (A+B) \times C=A \times C + B \times C \end{equation} \label{itx_iop8} \]

乘法右分配律：

\[ \begin{equation} C \times (A +B) = C \times A + C \times B \end{equation} \label{itx_iop9} \]

对数乘的结合性：

\[ \begin{equation} k \times (A \times B) = (k \times A) \times B = A \times (k \times B) \end{equation} \label{itx_iop10} \]

Haramard乘积：矩阵相同位置相乘，产生新矩阵用\(A \odot B\)表示：

\[ \begin{equation} A \odot B = \begin{pmatrix} a_{11} \times b_{11} & a_{12} \times b_{12} & \cdots & a_{1j} \times b_{1j} \\ a_{21} \times b_{21} & a_{22} \times b_{22} & \cdots & a_{2j} \times b_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} \times b_{i1} & a_{i2} \times b_{i2} & \cdots & a_{ij} \times b_{ij} \end{pmatrix} \end{equation} \label{itx_hdm} \]

转置矩阵（tranposed matrix）：把单个矩阵\(A\)内部的元素\(a_{ij}\)与\(a_{ji}\)互换， 记作\(^{\mathrm{T}}A\)或是\(A^{\mathrm{T}}\)（在关于神经网络的文献中， 转置矩阵有不同写法\(^{\mathrm{t}}A\)、\(A^{\mathrm{t}}\)、 \(^{\top}A\)、\(A^\top\)等等，要特别留意。）：

\[ \begin{equation} A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1j} \\ a_{21} & a_{22} & \cdots & a_{2j} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{ij} \\ \end{pmatrix} , A^{\mathrm{T}} = \begin{pmatrix} a_{11} & a_{21} & \cdots & a_{i1} \\ a_{12} & a_{22} & \cdots & a_{i2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1j} & a_{2j} & \cdots & a_{ij} \\ \end{pmatrix} \end{equation} \label{itx_ts} \]

矩阵的线性变换

对于某种变换\(T\)，如果多个向量无论在变换之前还是之后相加， 如果产生的结果向量都相同，那么这种变换\(T\)就被称为「线性变换」 （Liner Tranformation Definition）。

线性变换定义参考：\(\eqref{vct_lntsf}\)

向量的旋转、镜像翻转、拉伸操作都是线性变换。 我们可以把多个向量相加，然后再旋转、镜像翻转、拉伸； 或者把每个向量分别旋转、镜像翻转、拉伸，然后再相加。 这二者最后生成的结果向量都是相同的。

例如，我们要定义一套新的变换名字叫\(MyTrans\)。它会对向量进行以下变换：

1. 在\(y=-x\)这个镜面上进行翻转。
2. 在\(z\)轴上向正方向拉伸2倍。

得到变换的矩阵

先假设一个最简单向量\((1,1,1)\)，它在每个维度上都是\(+1\)。可以分解为三个向量相加：

\[ \begin{equation} \begin{pmatrix} 1 \\ 1 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 1 \\ \end{pmatrix} \end{equation} \label{vct_liner_tran_samp_st01} \]

然后再把\(MyTrans\)这个变换应用到每一个维度上。

先看\(x\)这个维度：

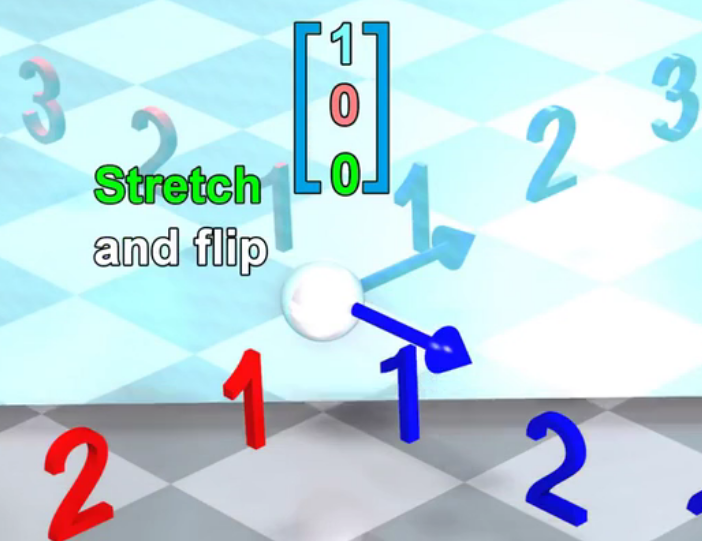
按照第一步：在\(y=-x\)这个镜面翻转后得到：

按照第二步：在\(z\)轴上向拉伸2倍不会对这个向量生成任何变化。 所以整个\(MyTrans\)在\(x\)这个维度上最终的变换结果就是：

\[ \begin{equation} \begin{pmatrix} 0 \\ -1 \\ 0 \\ \end{pmatrix} \end{equation} \label{vct_liner_tran_samp_st02} \]

然后是\(y\)这个维度：

按照第一步：在\(y=-x\)这个镜面翻转后得到：

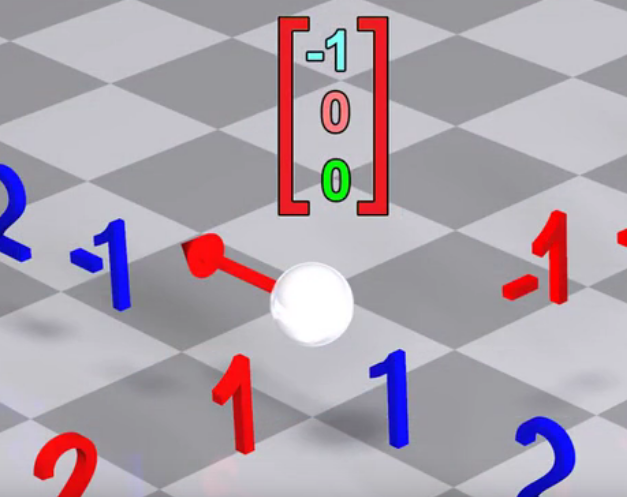
按照第二步：在\(z\)轴上向拉伸2倍不会对这个向量生成任何变化。 所以整个\(MyTrans\)在\(y\)这个维度上最终的变换结果就是：

\[ \begin{equation} \begin{pmatrix} -1 \\ 0 \\ 0 \\ \end{pmatrix} \end{equation} \label{vct_liner_tran_samp_st03} \]

最后的\(z\)这个维度，它在按照第一步：在\(y=-x\)这个镜面翻转后不会有任何变化， 但是在在\(z\)轴上向拉伸2倍会得到：

\[ \begin{equation} \begin{pmatrix} 0 \\ 0 \\ 2 \\ \end{pmatrix} \end{equation} \label{vct_liner_tran_samp_st04} \]

把三个维度的变换结果排在一起，就是：

\[ \begin{equation} \begin{pmatrix} 0 \\ -1 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} -1 \\ 0 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 2 \\ \end{pmatrix} \end{equation} \label{vct_liner_tran_samp_st05} \]

可以把本个维度的向量记为一个矩阵，每一行代表一个一个维度向量的变换的方式：

\[ \begin{equation} \begin{pmatrix} 0 & -1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 2 \\ \end{pmatrix} \end{equation} \label{vct_liner_tran_samp_st05tm} \]

这个矩阵就代表了我们定义的\(MyTrans\)变换，可以把它套用在其他的向量上。

把变换矩阵套用在向量上

例如我们要对一个向量\((5,6,7)\)进行\(MyTrans\)变换， 则把这三个值分别乘变换矩阵里代表维度的三行：

\[ \begin{equation} \begin{split} & 5 \times \begin{pmatrix} 0 \\ -1 \\ 0 \\ \end{pmatrix} + 6 \times \begin{pmatrix} -1 \\ 0 \\ 0 \\ \end{pmatrix} + 7 \times \begin{pmatrix} 0 \\ 0 \\ 2 \\ \end{pmatrix} \\ =& \begin{pmatrix} 0 \\ -5 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} -6 \\ 0 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 14 \\ \end{pmatrix} \\ =& \begin{pmatrix} -6 \\ -5 \\ 14 \\ \end{pmatrix} \end{split} \end{equation} \label{vct_liner_tran_samp_st06} \]

同样在地，如果我们要对另一个向量\((0,5,0)\)进行\(MyTrans\)变换，则：

\[ \begin{equation} \begin{split} & 0 \times \begin{pmatrix} 0 \\ -1 \\ 0 \\ \end{pmatrix} + 5 \times \begin{pmatrix} -1 \\ 0 \\ 0 \\ \end{pmatrix} + 0 \times \begin{pmatrix} 0 \\ 0 \\ 2 \\ \end{pmatrix} \\ =& \begin{pmatrix} 0 \\ -5 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \\ \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \\ \end{pmatrix} \\ =& \begin{pmatrix} 0 \\ -5 \\ 0 \\ \end{pmatrix} \end{split} \end{equation} \label{vct_liner_tran_samp_st07} \]

导数

对于函数\(f(x)\)，prime符号\('\)表示表示导函数，Delta符号\(\Delta\)表示\(\Delta x\) 无限趋近于\(0\)：

\[ \begin{equation} f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \end{equation} \label{pf_def1} \]

如果\(\Delta x\)无限接近于\(0\)，则点\(Q\)无限接近于点\(P\)，\(PQ\)所在的直线无限接近于 \(f'(x)\)所在的直线：

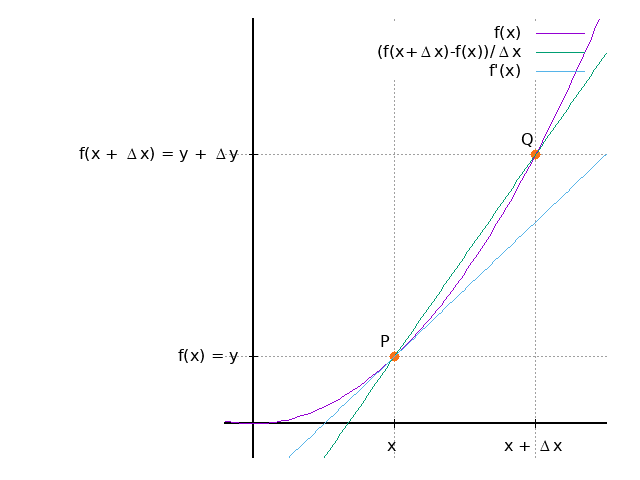
已知函数\(f(x)\)，求导函数\(f'(x)\)，称为对函数\(f(x)\)「求导」。当\(\ref{pf_def1}\) 的值存在时，称函数\(f(x)\)「可导」。

例，求导\(f(x)=3x\)：

\[ f'(x) = \lim_{\Delta x \to 0} \frac{3(x+\Delta x) -3x}{\Delta x} = \lim_{\Delta x \to 0} \frac{3\Delta x}{\Delta x} = \lim_{\Delta x \to 0} 3 = 3 \]

例，求导\(f(x)=x^2\)：

\[ f'(x) = \lim_{\Delta x \to 0} \frac{(x+\Delta x)^2 -x^2}{\Delta x} = \lim_{\Delta x \to 0} \frac{2x\Delta x + (\Delta x)^2}{\Delta x} = \lim_{\Delta x \to 0} (2x + \Delta x) = 2x \]

导数的分数形式

导函数还可以用分数的形式来表示：

\[ \begin{equation} f'(x) = \frac{{\rm d} y}{{\rm d} x} \end{equation} \label{pf_def2} \]

可以像分数一样进行约分等操作。

常用求导公式

求导过程不一定套用公式\(\ref{pf_def1}\)，常用函数的导函数可以背出来。

常数的导数，当\(c\)为常数：

\[ \begin{equation} c'=0 \end{equation} \label{pf_pf1} \]

幂函数的导数：

\[ \begin{equation} (x^a)'= ax^{a-1} \end{equation} \label{pf_pf2} \]

指数函数的导数：

\[ \begin{equation} (a^x)'= a^x \ln a \end{equation} \label{pf_pf3-1} \] \[ \begin{equation} (e^x)' = e^x \end{equation} \label{pf_pf3-2} \] \[ \begin{equation} (e^{-x})'= -e^{-x} \end{equation} \label{pf_pf3-3} \]

对数函数的导数：

\[ \begin{equation} (\log_ax)' = \frac{1}{x\ln a} \end{equation} \label{pf_pf4-1} \] \[ \begin{equation} (\ln x)' = \frac{1}{x} \end{equation} \label{pf_pf4-2} \]

三角函数的导数：

\[ \begin{equation} (\sin x)' = \cos x \end{equation} \label{pf_pf5-1} \] \[ \begin{equation} (\cos x)' = - \sin x \end{equation} \label{pf_pf5-2} \] \[ \begin{equation} (\tan x)' = \frac{1}{\cos x}^2 = (sec x)^2 \end{equation} \label{pf_pf5-3} \] \[ \begin{equation} (\cot x)' = - \frac{1}{\sin x}^2 = -(\csc x)^2 \end{equation} \label{pf_pf5-4} \] \[ \begin{equation} (\sec x)' = \sec x \cdot \tan x \end{equation} \label{pf_pf5-5} \] \[ \begin{equation} (\csc x)' = - \csc x \cdot \cot x \end{equation} \label{pf_pf5-6} \] \[ \begin{equation} (\arcsin x)' = (\arccos x)' = \frac{1}{\sqrt{1-x^2}} \end{equation} \label{pf_pf5-7} \] \[ \begin{equation} (\arctan x)' = ({\rm arccot} \, x)' = \frac{1}{1-x^2} \end{equation} \label{pf_pf5-8} \]

导数的性质

导数加、减、乘常数\(c\)具有「线性性」：

\[ \begin{equation} \begin{split} (f(x) + g(x))' &= f'(x) + g'(x) \\ (f(x) - g(x))' &= f'(x) - g'(x) \\ (cf(x))' &= cf'(x) \end{split} \end{equation} \label{pf_pfp-1} \]

导数的线性性是「误差反向传播法」重要元素。

导数之间乘除法：

\[ \begin{equation} \begin{split} (f(x) \times g(x))' &= f'(x)g(x) + f(x)g'(x) \\ (\frac{f(x)}{g(x)})' &= \frac{f'(x)g(x) - f(x)g'(x)}{f(g)^2} \end{split} \end{equation} \label{pf_pfp-2} \]

例，当\(f(x)=(2-x)^2\)时：

\[ \begin{split} f'(x) &= (4-4x+x^2)' = 4' - 4(x)'+ (x^2)' \\ &= 0 - 4 \times 1 + 2x = -4 + 2x \end{split} \]

例，当\(f(x)=2x^2+3x+1\)时：

\[ \begin{split} f'(x) &= (2x^2)'+(3x)'+(1)' \\ & = 2(x^2)'+3(x)'+(1)' = 4x + 3 \end{split} \]

例，当\(f(x)=1+e^{-x}\)时：

\[ f'(x) = (1)' + (e^{-x})' = -e^{-x} \]

分数函数的导数

当\(f(x) \neq 0\)时：

\[ \begin{equation} (\frac{1}{f(x)})' = \frac{f'(x)}{(f(x))^2} \end{equation} \label{pf_frac} \]

Sigmoid函数的导数

\[ \begin{equation} \begin{split} \sigma ' (x) &= (\frac{1}{1 + e^{-x}})' = \frac{(1 + e^{-x})' }{(1 + e^{-x})^2} = \frac{e^{-x} }{(1 + e^{-x})^2} \\ &= \frac{1 + e^{-x}-1 }{(1 + e^{-x})^2} = \frac{1+e^{-x}}{ (1+e^{-x})^2} - \frac{1}{(1+e^{-x })^2} \\ &= \frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x })^2} \\ &= \sigma(x) - \sigma(x)^2 \\ &= \sigma(x)(1 - \sigma(x)) \end{split} \end{equation} \label{pf_sigmoid} \]

最小值

• 充分条件：当函数\(f(x)\)在\(x=a\)处时为最小值，那么\(f(a)=0\)。
• 必要条件：\(f(a)=0\)是函数\(f(x)\)在\(x=a\)处时为最小值的必要条件。

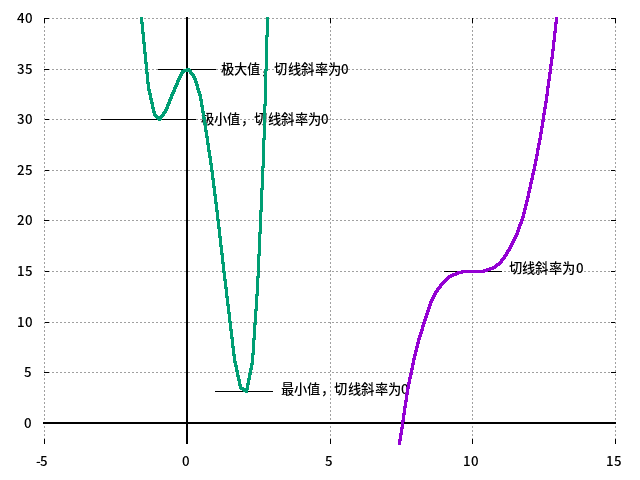
例，为了得到函数\(f(x)=3x^4-4x^3-12x^2+32\)的最值与极值，需要先求导：

\[ f'(x)=12x^3-12x^2-24x=12x(x+1)(x-2) \]

x	<-1	-1	(-1,0)	0	(0,2)	2	>2
f'(x)	<0	0	>0	0	<0	0	>0
f(x)	递减	27	递增	3	递减	0	递增
		极小		极大		最小

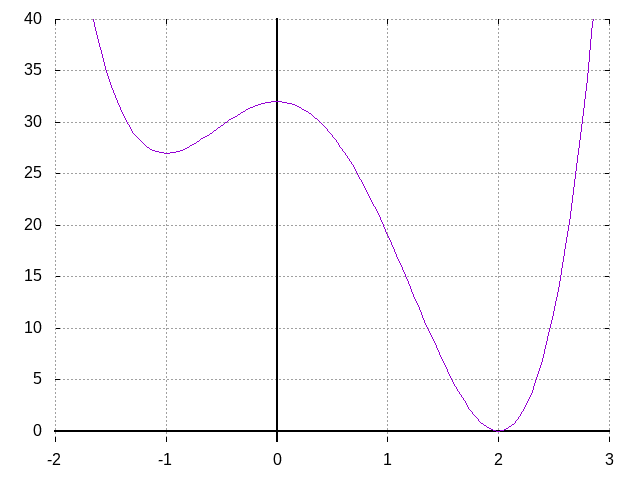
例，为了得到函数\(f(x)=2x^2-4x+3\)的最值与极值，需要先求导：

\[ f'(x)=4x-4 \]

x	<1	1	>1
f'(x)	<0	0	>0
f(x)	递减	1	递增
		最小

偏导函数

多变量函数

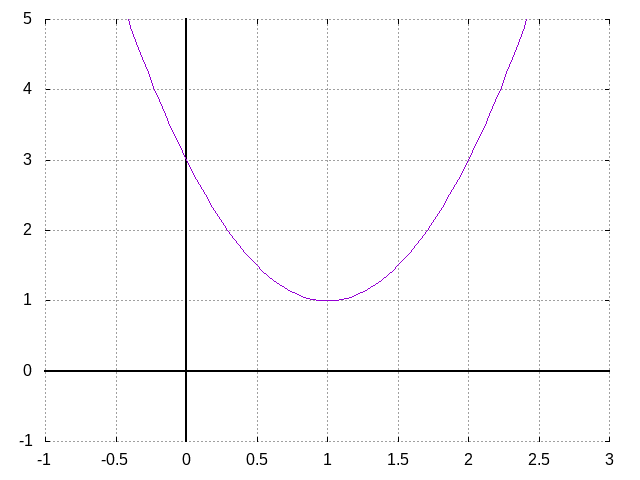
单变量函数\(y=f(x)\)中，\(x\)称为自变量，\(y\)称为因变量。而多变量函数有多个变量， 比如二个变量\(f(x,y)=x^2+y^2\)：

甚至更多个：\(f(x_1,x_2, \cdots, x_n)\)

偏导数

「偏导数」（partial derivative）是指针对多变量函数的多个变量中指定的 一个变量进行求导。

例如\(f'(x,y)\)把\(x\)视为变量，把\(y\)视为常量然后求导。得到的导数称为 「关于\(x\)的偏导数」（partial derivative of \(f(x,y)\) with respect to \(x\)）。 用符号表示为：

\[ \begin{equation} \frac{\partial z}{\partial x} = \frac{\partial f(x,y)}{\partial x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x,y)-f(x,y)}{\Delta x} \end{equation} \label{pdf_fcx} \]

同理关于\(y\)的偏导数：

\[ \begin{equation} \frac{\partial z}{\partial y} = \frac{\partial f(x,y)}{\partial y} = \lim_{\Delta x \to 0} \frac{f(x,y+\Delta y)-f(x,y)}{\Delta y} \end{equation} \label{pdf_fcy} \]

例，偏导数应用到神经网络中的函数\(f(x,y)=3x^2+4y^2\)：

\[ \frac{\partial f(x,y)}{\partial x}=6x \quad \quad , \quad \quad \frac{\partial f(x,y)}{\partial y}=8y \]

例，偏导数应用到神经网络中的函数\(z=wx+b\)：

\[ \frac{\partial z}{\partial x}=w \quad \quad , \quad \quad \frac{\partial z}{\partial w}=x \quad \quad , \quad \quad \frac{\partial z}{\partial b}=1 \]

例，偏导数应用到神经网络中的函数\(z=w_1x_1+w_2x_2+b\)：

\[ \frac{\partial z}{\partial x_1}=w_1 \quad \quad , \quad \quad \frac{\partial z}{\partial w_2}=x_2 \quad \quad , \quad \quad \frac{\partial z}{\partial b}=1 \]

偏导的几何意义与梯度

梯度（gradient）这个概念可以先把它想像成山坡的坡度和方向。

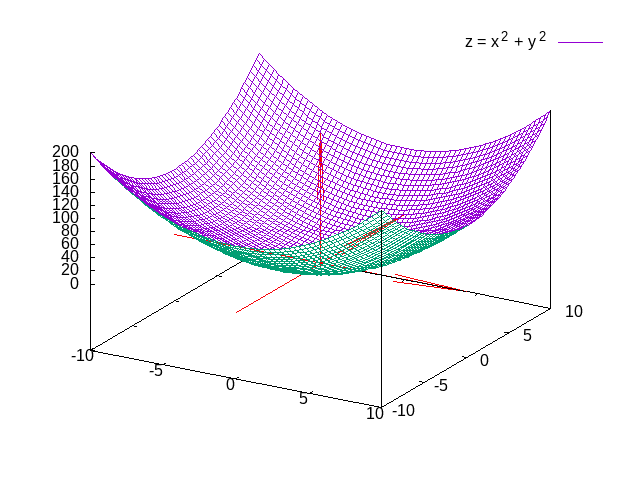
以函数\(f(x,y)=z\)的三维图像为例：

函数图像上的每一个点都有一个梯度。如果用向量来表示这个梯度：

• 向量方向代表坡度（\(z\)值）增加的方向。
• 向量的大小代表坡度的陡峭程度。

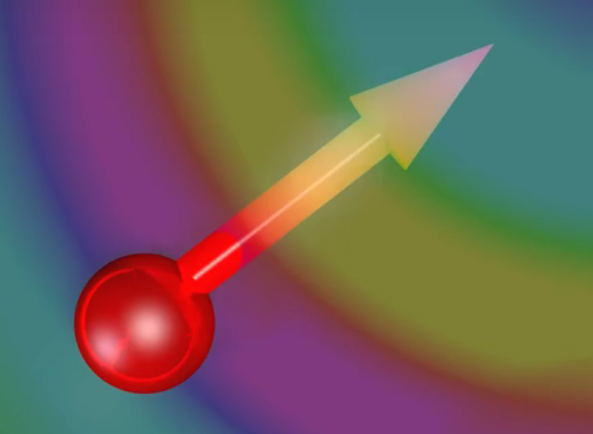
首先来理解一下偏导数的几何意义。

函数\(f(x,y)=a\)的图像有三个维度(x,y,z)。如果我们把\(x\)限制为一个固定值， 那么随着\(y\)的变化，\(z\)的值也会相应地变化。

\(z\)的变化值除以\(y\)的变化值\(\frac{\Delta z}{\Delta y}\)就是\(z\)的斜率也会随之变化：

所以在函数图像这个曲面上的每一个点：

• 都存在\(y\)固定而\(x\)变化的偏导\(\frac{\partial z}{\partial x}\)
• 也都有\(x\)固定而\(y\)变化的偏导\(\frac{\partial z}{\partial y}\)；

如果我们用向量来表示斜率：方向的正负对应斜率的正负，大小对应斜率的大小：

那么函数的每个点上都有\(x\)与\(y\)偏导的两个向量：

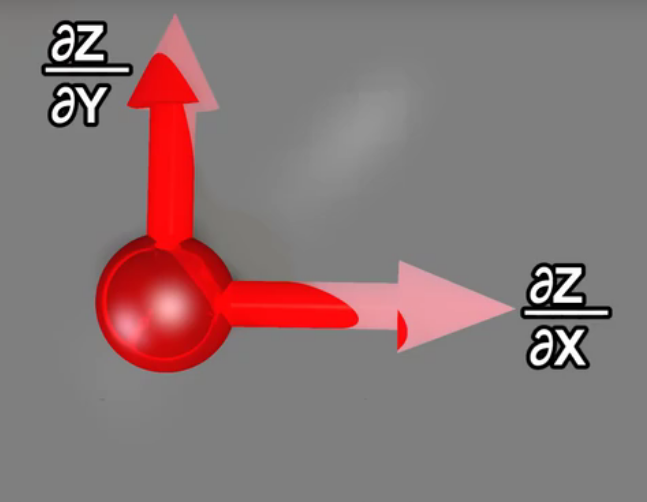
这两个向量相加就得到了一个新的向量，代表这个点上函数的梯度：

多变量函数的最小值条件

函数\(z=f(x,y)\)取得最小值的必要条件是：

\[ \begin{equation} \frac{\partial f}{\partial x}=0,\frac{\partial f}{\partial y}=0 \end{equation} \label{pdf_mvmm} \]

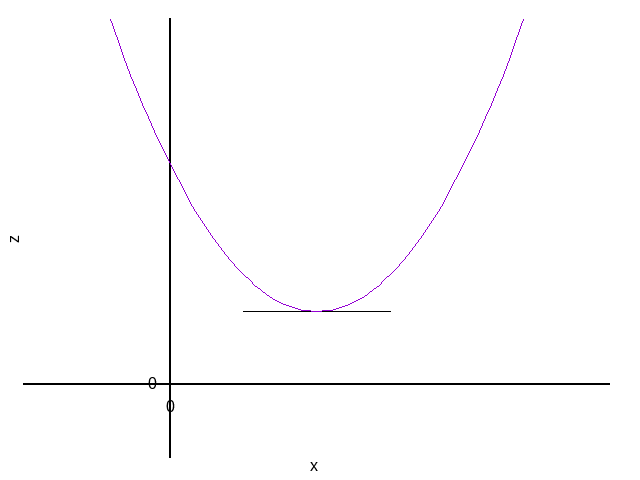
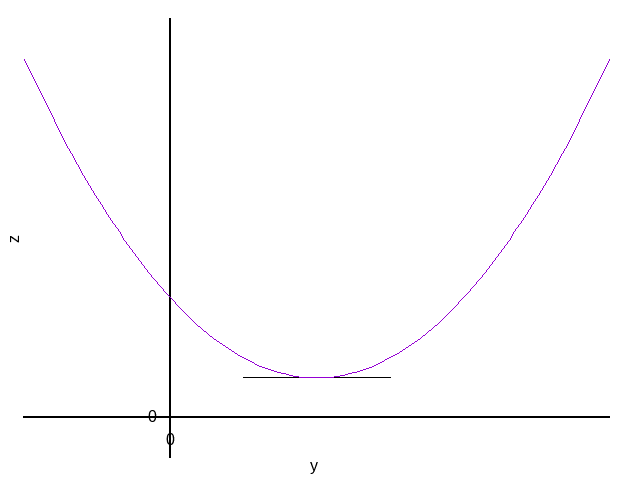
例，求\(z=x^2+y^2\)最小值时的\(x\)与\(y\)的值：

先求偏导：

\[ \frac{\partial z}{\partial x}=2x \quad \quad , \quad \quad \frac{\partial z}{\partial y}=2y \]

可知最小值的必要条件是\(x=0,y=0\)，而此时\(z=0\)。 由于\(z=x^2+y^2 \geq 0\)，所以\(x=0,y=0,z=0\)必然为最小值。

拉格朗日乘数法

在实际的最小值问题中（比如求性能良好的神经网络正则化技术中）， 有时会对变量附加约束条件，例如当\(x^2+y^2=1\)时，求\(x+y\)的最小值。 这种情况下可以使用「拉格朗日乘数法」：

首先引入参数\(\lambda\)，创建如下形式的函数\(L\)：

\[ \begin{equation} L=f(x,y)-\lambda g(x,y)=(x+y)-\lambda(x^2+y^2-1) \end{equation} \label{pdf_lglrpd} \]

然后求偏导：

\[ \begin{equation} \frac{\partial L}{\partial x}=1-2\lambda x = 0 \quad \quad , \quad \quad \frac{\partial L}{\partial y}=1-2\lambda y = 0 \end{equation} \label{pdf_lglrxy} \]

然后结合约束条件\(x^2+y^2=1\)，得到：

\[ \begin{equation} x=y=\lambda=\pm \frac{1}{\sqrt{2}} \end{equation} \label{pdf_lglrrs} \]

因而当\(x=y=-\frac{1}{\sqrt{2}}\)时，\(x+y\)取得最小值\(-\sqrt{2}\)。