神经网络数学基础.Part.02

数学基础 Part 02

链式法则

复合函数

当\(u=g(x)\)，\(y=f(u)\)，\(y\)作为\(x\)的函数可以表示为\(y=f(g(x))\)的「复合函数」形式。

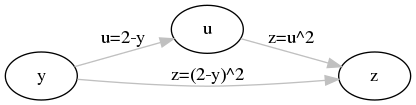
例：\(z=(2-y)^2\)是\(u=2-y\)和\(z=u^2\)的复合函数：

例：激活函数\(a(x)\)有多个输入\(x_1,x_2,x_3,\cdots,x_n\)，则神经单元输出\(y\)的过程：

\[ \begin{cases} \begin{split} z &= f(x_1,x_2,x_3,\cdots,x_n)=w_1x_1+w_2x_2+w_3x_3+\cdots +w_nx_n+b \\ y &= a(z) \end{split} \end{cases} \]

单变量函数的链式法则

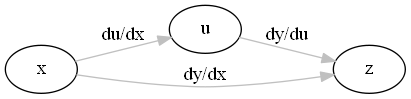
当\(u=g(x)\)，\(y=f(u)\)时，复合函数\(y=f(g(x))\)的导数可以使用以下「复合函数求导公式」 也叫「链式法则」：

\[ \begin{equation} \frac{{\rm d}y}{{\rm d}x}=\frac{{\rm d}y}{{\rm d}u}\frac{{\rm d}u}{{\rm d}x} \end{equation} \label{rpc_chnfp} \]

公式\(\ref{rpc_chnfp}\)当作分数来看，右边约分去掉\(\rm{d}u\)也等于左边。 （注：这个约分方法不适用于\(\rm{d}x\)、\(\rm{d}y\)平方地场景）

例：\(y=f(u)\)，\(u=f(v)\)，\(v=f(x)\)时，求导：

\[ \begin{equation} \frac{{\rm d}y}{{\rm d}x}=\frac{{\rm d}y}{{\rm d}u}\frac{{\rm d}u}{{\rm d}v}\frac{{\rm d}v}{{\rm d}x} \end{equation} \label{rpc_chnfp2} \]

例：对于以下\(x\)的函数求导：

\[ \frac{1}{1 + {\rm e}^{-(wx+b)}} \quad w \text{、} b \text{为常数} \]

解：设\(wx+b=u\)，可以得到：

\[ \frac{1}{1 + {\rm e}^{-u}} \quad \text{，} u=wx+b \]

前一部分是Sigmoid函数，之前已经求过Sigmoid函数的导函数：

\[ \frac{{\rm d}y}{{\rm d}u} = y(1-y) \]

再代入\(\frac{{\rm d}u}{{\rm d}x}=w\)，得到：

\[ \begin{equation} \begin{split} \frac{{\rm d}x}{{\rm d}u} &= \frac{{\rm d}y}{{\rm d}u}\frac{{\rm d}u}{{\rm d}x} \\ &= y(1-y) \cdot w \\ &= \frac{1}{1+{\rm e}^{(wx+b)}} \Big(1 - \frac{1}{1+{\rm e}^{(wx+b)}}\Big) \cdot w \\ &= \frac{w}{1+{\rm e}^{(wx+b)}} \Big(1 - \frac{1}{1+{\rm e}^{(wx+b)}}\Big) \end{split} \end{equation} \]

多变量函数的链式法则

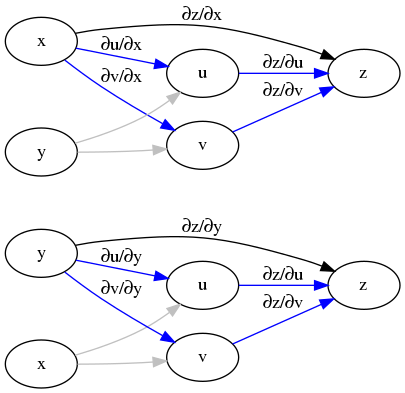
对于函数\(z(u,v)\)，\(u(x,y)\)，\(v(x,y)\)，求导：

\[ \begin{equation} \frac{\partial z}{\partial x}= \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x} \quad , \quad \frac{\partial z}{\partial y}= \frac{\partial z}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial y} \end{equation} \label{rpc_mmcpcf} \]

例，\(C=u^2+v^2\)，\(u=ax+by\)，\(v=px+qy\)，（\(a,b,q,p\)为常数）时，导数为：

\[ \begin{split} \frac{\partial C}{\partial x} &= \frac{\partial C}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial C}{\partial v} \frac{\partial v}{\partial x} & = 2u \times a + 2v \times p \\ & &= 2(ax+by) \times a + 2(px+qy) \times p \\ & &= 2a(ax+by) + 2p(px+qy) \\ \frac{\partial C}{\partial y} &= \frac{\partial C}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial C}{\partial v} \frac{\partial v}{\partial y} & = 2u \times b + 2v \times q \\ & &= 2(ax+by) \times b + 2(px+qy) \times q \\ & &= 2b(ax+by) + 2q(px+qy) \\ \end{split} \]

还可以扩展到更多变量的情况下，例如当\(a1,b1,c1,a2,b2,c2,a3,b3,c3\)为常数时：

\[ \begin{cases} \begin{split} C &= u^2 + v^2 + w^2 \\ u &= a_1x + b_1y + c_1z \\ v &= a_2x + b_2y + c_2z \\ w &= a_2x + b_2y + c_2z \end{split} \end{cases} \]

上面式子的导数为：

\[ \begin{split} \frac{\partial C}{\partial x} & = \frac{\partial C}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial C}{\partial v} \frac{\partial v}{\partial x} + \frac{\partial C}{\partial w} \frac{\partial w}{\partial x} \\ & = 2u \times a_1 + 2v \times a_2 + 2w \times a_3 \\ & = 2(a_1x+a_1y+a_1z) \times a_1 + 2(a_2x+a_2y+a_2z) \times a_2 + 2(a_3x+a_3y+a_3z) \times a_3 \\ & = 2a_1(a_1x+a_1y+a_1z) + 2a_2(a_2x+a_2y+a_2z) + 2a_3(a_3x+a_3y+a_3z) \\ & \\ \frac{\partial C}{\partial y} & = \frac{\partial C}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial C}{\partial v} \frac{\partial v}{\partial y} + \frac{\partial C}{\partial w} \frac{\partial w}{\partial y} \\ & = 2u \times b_1 + 2v \times b_2 + 2w \times b_3 \\ & = 2(a_1x+a_1y+a_1z) \times b_1 + 2(a_2x+a_2y+a_2z) \times b_2 + 2(a_3x+a_3y+a_3z) \times b_3 \\ & = 2b_1(a_1x+a_1y+a_1z) + 2b_2(a_2x+a_2y+a_2z) + 2b_3(a_3x+a_3y+a_3z) \\ & \\ \frac{\partial C}{\partial z} & = \frac{\partial C}{\partial u} \frac{\partial u}{\partial z} + \frac{\partial C}{\partial v} \frac{\partial v}{\partial z} + \frac{\partial C}{\partial w} \frac{\partial w}{\partial z} \\ & = 2u \times c_1 + 2v \times c_2 + 2w \times c_3 \\ & = 2(a_1x+a_1y+a_1z) \times c_1 + 2(a_2x+a_2y+a_2z) \times c_2 + 2(a_3x+a_3y+a_3z) \times c_3 \\ & = 2c_1(a_1x+a_1y+a_1z) + 2c_2(a_2x+a_2y+a_2z) + 2c_3(a_3x+a_3y+a_3z) \\ \end{split} \]

函数的近似公式

多变量函数的近似公式是实现梯度下降的工具。

单变量函数的近似公式

在求导的定义中，\(\Delta x\)是趋近于「无限小」：

\[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]

如果把「无限小」换成「非常微小」，也不会带来很大的误差，从而得到 ：

\[ \begin{equation} f'(x) \fallingdotseq \frac{f(x + \Delta x) - f(x)}{\Delta x} \end{equation} \label{pf_lmll} \]

进一步变形为「单变量函数的近似公式」：

\[ \begin{equation} \begin{split} f'(x) & \fallingdotseq \frac{f(x + \Delta x) - f(x)}{\Delta x} \\ f'(x) \cdot \Delta x & \fallingdotseq f(x + \Delta x) - f(x) \\ f'(x) \cdot \Delta x + f(x) & \fallingdotseq f(x + \Delta x) \\ f(x + \Delta x) & \fallingdotseq f(x) + f'(x)\Delta x \\ \end{split} \end{equation} \label{pf_lmll2} \]

例，\(f(x)=e^x\)在\(x=0\)时的近似公式：

\[ e^{x + \Delta x} \fallingdotseq e^x + e^x\Delta x \]

当\(x=0\)时，把\(\Delta x\)替换为\(x\)：

\[ e^{x} \fallingdotseq 1 + x \]

从图像上看，\(f(x)=e^x\)与\(f(x)=1+x\)在\((0,1)\)处重叠：

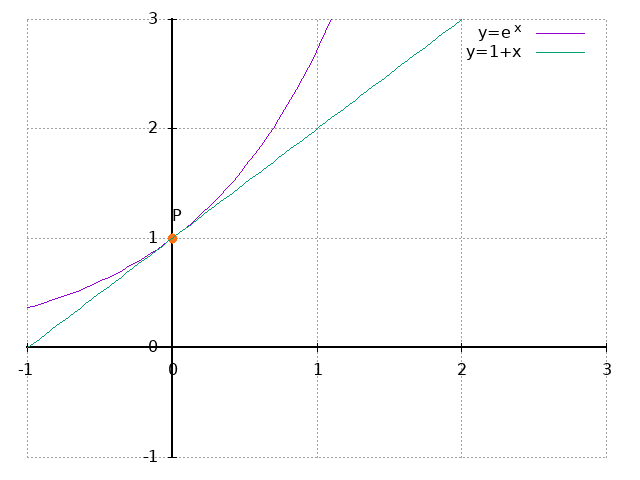
多变量函数的近似公式

把近似公式扩展到多变量环境下：

\[ \begin{equation} f(x+\Delta x,y+\Delta y) \fallingdotseq f(x,y) + \frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x,y)}{\partial y}\Delta y \end{equation} \label{pf_lmml} \]

例，\(z=e^{x+y}\)时，求\(x=y=0\)附近的近似公式：

根据指数函数的求导公式：

\[ \frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}=e^{x+y} \]

与近似值公式结合，得到：

\[ e^{x+\Delta x+y+\Delta y} \fallingdotseq e^{x+y} +e^{x+y}\Delta x + e^{x+y}\Delta y \]

当\(x=y=0\)时，把\(\Delta x\)替换为\(x\)，\(\Delta y\)替换为\(y\)：

\[ e^{x+y} \fallingdotseq 1+x+y \]

公式\(\ref{pf_lmml}\)可以进一步简化，首先定义\(\Delta z\)，用于表示当\(x\)、\(y\) 依次变化\(\Delta x\)、\(\Delta y\)时函数\(z=f(x,y)\)的变化：

\[ \begin{equation} \Delta z = f(x+\Delta x,y+\Delta y) - f(x,y) \end{equation} \label{pf_lmml2} \]

然后公式\(\ref{pf_lmml}\)就可以简化为：

\[ \begin{split} f(x+\Delta x,y+\Delta y) & \fallingdotseq f(x,y) + \frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x,y)}{\partial y}\Delta y \\ f(x+\Delta x,y+\Delta y) - f(x,y) & \fallingdotseq \frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x,y)}{\partial y}\Delta y \\ \Delta z & \fallingdotseq \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y \end{split} \label{pf_lmml3} \]

当需要扩展到更多变量时：

\[ \begin{equation} \Delta z \fallingdotseq \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y + \frac{\partial z}{\partial w}\Delta w \end{equation} \label{pf_lmml5} \]

近似公式的向量表示

近似公式\(\ref{pf_lmml5}\)可以写成以两个向量内积的形式

\[ \begin{equation} \begin{split} \Delta z & \fallingdotseq \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y + \frac{\partial z}{\partial w}\Delta w \\ & \fallingdotseq \Big( \frac{\partial z}{\partial x} , \frac{\partial z}{\partial y} , \frac{\partial z}{\partial w}\Big) \cdot (\Delta x , \Delta y , \Delta z) \\ \end{split} \end{equation} \label{pf_lmml5b} \]

如果变量变得非常多，那么\(\ref{pf_lmml5b}\)这个公式会写得非常长。 为了表达简单我们把这两个变量分别起两个缩写名字：\(\nabla z\)和\(\Delta x\)， （\(\nabla\)读作nabla）：

\[ \begin{equation} \begin{split} \nabla z &= \Big( \frac{\partial z}{\partial x} , \frac{\partial z}{\partial y} , \frac{\partial z}{\partial z}\Big) \\ \Delta x &= (\Delta x , \Delta y , \Delta z) \end{split} \end{equation} \label{pf_lmml5c} \]

这样再长的公式\(\ref{pf_lmml5b}\)也只要写成：

\[ \begin{equation} \Delta z = \nabla z \times \Delta x \end{equation} \label{pf_lmml6} \]

泰勒展开式

「泰勒展开式」是近似公式一般化的公式：

\[ \begin{equation} \label{pf_lmmtl} \begin{split} & f(x + \Delta x, y + \Delta y) \\ = & f(x,y) + \frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y + \\ & \frac{1}{2!} \bigg \{ \frac{\partial ^2 f}{\partial x^2}(\Delta x)^2 + 2\frac{\partial ^2 f}{\partial x\partial y}\Delta x \Delta y + \frac{\partial ^2 f}{\partial y^2}(\Delta y)^2 \bigg \} + \\ & \frac{1}{3!} \bigg \{ \frac{\partial ^3 f}{\partial x^3}(\Delta x)^3 + 3\frac{\partial ^3 f}{\partial x^2\partial y}(\Delta x)^2 \Delta y + 3\frac{\partial ^3 f}{\partial x\partial y^2}\Delta x (\Delta y)^2 + \frac{\partial ^3 f}{\partial y^3}(\Delta y)^3 \bigg \} + \\ & \cdots \end{split} \end{equation} \]

从以上泰勒展开式中取出前三项，就得到多变量函数的近似公式\(\ref{pf_lmml}\)。

此外，我们约定：

\[ \frac{\partial ^2 f}{\partial x^2}=\frac{\partial}{\partial x}\frac{\partial f}{\partial x} , \quad \frac{\partial ^2 f}{\partial x \partial y}=\frac{\partial}{\partial x}\frac{\partial f}{\partial y} , \quad \cdots \]

梯度下降法

「梯度下降」法是用来寻找函数最小值的点的方法，同时也是神经网络要用到的重要工具。

目前我们只在函数充分光滑的前题下，讨论梯度下降法。

通过公式求最小值

对于一元函数\(y=f(x)\)要找最小值，那么\(f'(x)=0\)是满足最小值的必要条件。

那么对于二元函数\(z=f(x,y)\)的最小值，那么\(x\)与\(y\)取偏导都为\(0\)也是必要条件：

\[ \begin{equation} \frac{\partial f(x,y)}{\partial x}=0 , \quad \frac{\partial f(x,y)}{\partial y}=0 \end{equation} \label{fldl_pd2d} \]

从图像上来看，最小值所在的点也是函数图像的底部：

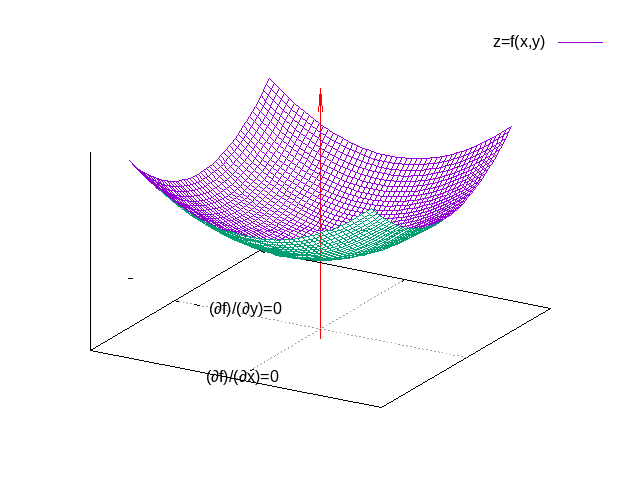
更多元的函数也是同理，分别求各个变量偏导函数值为\(0\)的点。

通过梯度下降法求最小值

但是，在实际问题中，要求得像\(\ref{fldl_pd2d}\)这样的联立方程式并不是容易的事情。 因此使用「梯度下降法」是更加现实的方案。

梯度下降法也叫「最速下降法」，模拟一个小球在重力作为下，从函数\(f(x,y)\)表面点 \(P(x,y,z)\)开始以最短路径下滑到最低点的过程。

在整个下滑的过程中的任意一个瞬间，小球所在的位置为 \(Q(x+\Delta x,y+\Delta y,z+\Delta z)\)：

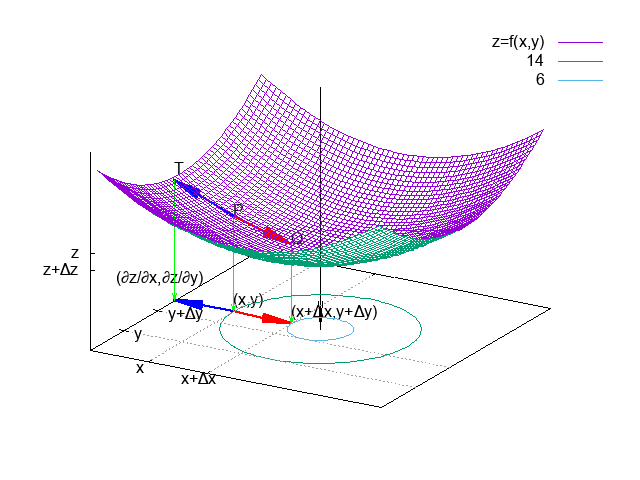
函数\(z=f(x,y)\)中，当\(x\)变动\(\Delta x\)，\(y\)变动\(\Delta y\)时，函数值\(z\)的变动 \(\Delta z\)：

\[ \Delta z = f(x+\Delta x, y+\Delta y)-f(x,y) \]

根据近似公式，可以简化为：

\[ \Delta z = \frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x,y)}{\partial y}\Delta y \]

近似公式可以用向量内积形式表示：

\[ \Bigg (\frac{\partial f(x,y)}{\partial x} , \frac{\partial f(x,y)}{\partial y}\Bigg ) \cdot (\Delta x , \Delta y) \]

而根据向量内积的定义\(a \cdot b=|a||b|\cos \theta\)可以得知，当\(\theta\)为\(180^\circ\) （即\(a\)与\(b\)两个向量方向相反）时内积的值最小，也意味\(\Delta z\) 最小。用公式 来表示就是：

\[ \begin{equation} b=-k \times a \quad \quad \text{$k$为正常数} \end{equation} \label{fldl_vtabrls} \]

把向量\(a\)与\(b\)的值代入\(\ref{fldl_vtabrls}\)就可以得到「梯度下降法的基本式」：

\[ \begin{equation} (\Delta x , \Delta y) = - \eta \Bigg (\frac{\partial f(x,y)}{\partial x} , \frac{\partial f(x,y)}{\partial y}\Bigg ) \quad \quad (\eta\text{为正的微小常量}) \end{equation} \label{fldl_sktl} \]

• \(\eta\)表示大0的微小常数。
• 等号左边的向量\((\Delta x , \Delta y)\)称为「位移向量」。

从点\((x,y)\)向\((x+\Delta x,y+\Delta y)\)移动时，如果满足公式\(\ref{fldl_sktl}\) 那么函数\(z=f(x,y)\)下降得最快。所以如下的向量：

\[ \begin{equation} \Bigg (\frac{\partial f(x,y)}{\partial x} , \frac{\partial f(x,y)}{\partial y}\Bigg ) \end{equation} \label{fldl_skpt} \]

称为函数\(f(x,y)\)在点\((x,y)\)处的梯度（gradient），它代表最陡的坡度方向。

例：函数\(z=x^2+y^2\)在点\((x,y)\)下降最快的向量\((\Delta x, \Delta y)\)。

先求偏导：

\[ \frac{\partial z}{\partial x} = 2x , \frac{\partial z}{\partial y} = 2y \]

然后把偏导代入梯度下降的基本式\(\ref{fldl_sktl}\)：

\[ (\Delta x , \Delta y) = - \eta \Bigg (\frac{\partial f(x,y)}{\partial x} , \frac{\partial f(x,y)}{\partial y}\Bigg ) \\ = - \eta (2x,2y) \quad \quad (\eta\text{为正的微小常量}) \]

题目中要求起点的位置是\((1,2)\)，得到

\[ (\Delta x , \Delta y) = - \eta (2 \times 1,2 \times 2) = - \eta (2,4) \quad \quad (\eta\text{为正的微小常量}) \]

多变量函数的梯度下降

梯度下降的基本式\(\ref{fldl_sktl}\)推广到多变量的条件下：

\[ \begin{equation} (\Delta x_1 , \Delta x_2, \cdots ,\Delta x_n) = - \eta \Bigg ( \frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2} , \frac{\partial f}{\partial x_1} , \cdots , \frac{\partial f}{\partial x_n} \Bigg ) \quad \quad (\eta\text{为正的微小常量}) \end{equation} \label{fldl_sktlm} \]

函数\(f\)在点\((x_1,x_2,\cdots,x_n)\)处的梯度：

\[ \begin{equation} \Bigg ( \frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2} , \frac{\partial f}{\partial x_1} , \cdots , \frac{\partial f}{\partial x_n} \Bigg ) \end{equation} \label{fldl_sktltl} \]

下降最短路径是从点\((x_1,x_2,\cdots,x_n)\)移动到 \((x_1+\Delta x_1,x_2+\Delta x_2,\cdots,x_n+\Delta x_n)\)。

哈密尔顿算子\(\nabla\)

在实际应用中函数的变量个数可能有成千上万个，书写时会用到哈密尔顿算子\(\nabla\)。 用\(\nabla f\)缩写：

\[ \begin{equation} \nabla f = \Bigg ( \frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2} , \frac{\partial f}{\partial x_3} , \cdots , \frac{\partial f}{\partial x_n} \Bigg ) \end{equation} \label{fldl_sknabla} \]

多变量梯度下降的基本式\(\ref{fldl_sktlm}\)简写为：

\[ \begin{equation} (\Delta x_1 , \Delta x_2, \cdots ,\Delta x_n) = - \eta \nabla f \quad \quad (\eta\text{为正的微小常量}) \end{equation} \label{fldl_sktlmnabla} \]

例如，对于二变量函数\(f(x,y)\)，梯度下降基本式简写为：

\[ (\Delta x , \Delta y) = - \eta \nabla f(x,y) \quad \quad (\eta\text{为正的微小常量}) \]

例如，对于三变量函数\(f(x,y,z)\)，梯度下降基本式简写为：

\[ (\Delta x , \Delta y, \Delta z) = - \eta \nabla f(x,y,z) \quad \quad (\eta\text{为正的微小常量}) \]

等号左边的向量\((\Delta x , \Delta y, \Delta z)\)称为「位移向量」， 也可以简化为\(\Delta x\)：

\[ \begin{equation} \Delta x = (\Delta x_1 , \Delta x_2, \cdots ,\Delta x_n) \end{equation} \label{fldl_skwl} \]

多变量梯度下降的基本式\(\ref{fldl_sktlm}\)可以更进一步简写为：

\[ \begin{equation} \Delta x = - \eta \nabla f \quad \quad (\eta\text{为正的微小常量}) \quad \quad (\eta\text{为正的微小常量}) \end{equation} \label{fldl_skwllabma} \]

\(\eta\)的取值

在神经网络中\(\eta\)称为「学习率」。从数学上来说，\(\eta\)是一个大于0的微小常量， 但是在计算机计算时，必须确定一个合适的值。而确定值大小的方法没有明确的方法， 往往只能反复试验。

用程序演示

以函数\(z=x^2+y^2\)为例，用梯度下降法求出\(z\)为最小值时的\((x,y)\)， 学习率采用\(\eta=0.1\)。

首先分别对\(x,y\)求导：

\[ \begin{split} \frac{\partial z}{\partial x}=2x , \frac{\partial z}{\partial y}=2y \end{split} \]

得到梯度：

\[ \begin{split} \Bigg (\frac{\partial z}{\partial x} , \frac{\partial z}{\partial y}\Bigg ) = (2x, 2y) \end{split} \]

然后根据梯度下降的基本式\(\ref{fldl_sktl}\)得到位移量：

\[ \begin{split} (\Delta x_i, \Delta y_i) &=- \eta \Bigg (\frac{\partial f(x,y)}{\partial x} , \frac{\partial f(x,y)}{\partial y}\Bigg ) \\ &=- \eta (2x_i,2y_i) \\ &= (- \eta \cdot 2x_i, - \eta \cdot 2y_i) \end{split} \]

下一轮的起点，用于开始新一轮的迭代：

\[ (x_{i+1},y_{i+1})=(x_i,y_i)+(\Delta x_i, \Delta y_i)=(x_i+\Delta x_i,y_i+\Delta y_i) \]

一直迭代直到最小值。用代码演示如下：

scala> val eta    = 0.1
scala> val func1  = (p: (Double, Double)) => Math.pow(p._1, 2) + Math.pow(p._2, 2)
scala> val funp1x = (x: Double) => 2 * x
scala> val funp1y = (y: Double) => 2 * y
scala> val start  = (3.0, 2.0)

scala> def acc(lst: List[String], idx: Int, max: Int, //
     |           eta: Double, curr: (Double, Double)): List[String] = {
     |   if (idx > max) lst else {
     |           val px = funp1x(curr._1)
     |           val py = funp1y(curr._2)
     |           val dx = px * -1 * eta
     |           val dy = py * -1 * eta
     |           val z = func1(curr)
     |           val nx = curr._1 + dx
     |           val ny = curr._2 + dy
     |           val node = (curr, (px, py), (dx, dy), z, (nx, ny))
     |           val str = f"${idx + 1}%02d    (${curr._1}%2.3f, ${curr._2}%2.3f)    " +
     |                   f"(${px}%2.3f, ${py}%2.3f)    " +
     |                   f"(${dx}%2.3f, ${dy}%2.3f)    " +
     |                   f"$z%2.3f"
     |           acc(str :: lst, idx + 1, max, eta, (nx, ny))
     |   }
     | }
acc: (lst: List[String], idx: Int, max: Int, eta: Double, curr: (Double, Double))List[String]

scala> println("迭代    起点           梯度           位移量       函数值")
scala> println("idx     (x,y)      (∂z/∂x,∂z/∂y)      (Δx,Δy)        z   ")
scala> println("---------------------------------------------------------")
scala> for (l <- acc(Nil, 0, 50, eta, start).reverse) println(l)

迭代    起点           梯度           位移量       函数值
idx     (x,y)      (∂z/∂x,∂z/∂y)      (Δx,Δy)        z   
---------------------------------------------------------
01  (3.000, 2.000) (6.000, 4.000) (-0.600, -0.400) 13.000
02  (2.400, 1.600) (4.800, 3.200) (-0.480, -0.320) 8.320
03  (1.920, 1.280) (3.840, 2.560) (-0.384, -0.256) 5.325
04  (1.536, 1.024) (3.072, 2.048) (-0.307, -0.205) 3.408
05  (1.229, 0.819) (2.458, 1.638) (-0.246, -0.164) 2.181
06  (0.983, 0.655) (1.966, 1.311) (-0.197, -0.131) 1.396
07  (0.786, 0.524) (1.573, 1.049) (-0.157, -0.105) 0.893
08  (0.629, 0.419) (1.258, 0.839) (-0.126, -0.084) 0.572
09  (0.503, 0.336) (1.007, 0.671) (-0.101, -0.067) 0.366
10  (0.403, 0.268) (0.805, 0.537) (-0.081, -0.054) 0.234
11  (0.322, 0.215) (0.644, 0.429) (-0.064, -0.043) 0.150
12  (0.258, 0.172) (0.515, 0.344) (-0.052, -0.034) 0.096
13  (0.206, 0.137) (0.412, 0.275) (-0.041, -0.027) 0.061
14  (0.165, 0.110) (0.330, 0.220) (-0.033, -0.022) 0.039
15  (0.132, 0.088) (0.264, 0.176) (-0.026, -0.018) 0.025
16  (0.106, 0.070) (0.211, 0.141) (-0.021, -0.014) 0.016
17  (0.084, 0.056) (0.169, 0.113) (-0.017, -0.011) 0.010
18  (0.068, 0.045) (0.135, 0.090) (-0.014, -0.009) 0.007
19  (0.054, 0.036) (0.108, 0.072) (-0.011, -0.007) 0.004
20  (0.043, 0.029) (0.086, 0.058) (-0.009, -0.006) 0.003
21  (0.035, 0.023) (0.069, 0.046) (-0.007, -0.005) 0.002
22  (0.028, 0.018) (0.055, 0.037) (-0.006, -0.004) 0.001
23  (0.022, 0.015) (0.044, 0.030) (-0.004, -0.003) 0.001
24  (0.018, 0.012) (0.035, 0.024) (-0.004, -0.002) 0.000
25  (0.014, 0.009) (0.028, 0.019) (-0.003, -0.002) 0.000
26  (0.011, 0.008) (0.023, 0.015) (-0.002, -0.002) 0.000
27  (0.009, 0.006) (0.018, 0.012) (-0.002, -0.001) 0.000
28  (0.007, 0.005) (0.015, 0.010) (-0.001, -0.001) 0.000
29  (0.006, 0.004) (0.012, 0.008) (-0.001, -0.001) 0.000
30  (0.005, 0.003) (0.009, 0.006) (-0.001, -0.001) 0.000
31  (0.004, 0.002) (0.007, 0.005) (-0.001, -0.000) 0.000
32  (0.003, 0.002) (0.006, 0.004) (-0.001, -0.000) 0.000
33  (0.002, 0.002) (0.005, 0.003) (-0.000, -0.000) 0.000
34  (0.002, 0.001) (0.004, 0.003) (-0.000, -0.000) 0.000
35  (0.002, 0.001) (0.003, 0.002) (-0.000, -0.000) 0.000
36  (0.001, 0.001) (0.002, 0.002) (-0.000, -0.000) 0.000
37  (0.001, 0.001) (0.002, 0.001) (-0.000, -0.000) 0.000
38  (0.001, 0.001) (0.002, 0.001) (-0.000, -0.000) 0.000
39  (0.001, 0.000) (0.001, 0.001) (-0.000, -0.000) 0.000
40  (0.000, 0.000) (0.001, 0.001) (-0.000, -0.000) 0.000 <- min x, y, z
41  (0.000, 0.000) (0.001, 0.001) (-0.000, -0.000) 0.000
42  (0.000, 0.000) (0.001, 0.000) (-0.000, -0.000) 0.000
43  (0.000, 0.000) (0.001, 0.000) (-0.000, -0.000) 0.000
44  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000
45  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000
46  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000
47  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000
48  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000
49  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000
50  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000
51  (0.000, 0.000) (0.000, 0.000) (-0.000, -0.000) 0.000

修正迭代的步长

位移量\(\Delta x\)在每次迭代的过程中并不是固定的大小，比如上面的例子里步长随着 迭代的次数越来越小。

在实际应用过程了，为了得到一个比较固定的步长，会对梯度下降的基本式\(\ref{fldl_sktl}\) 做一些修改：

\[ \begin{split} (\Delta x_i, \Delta y_i) =- \eta \Bigg (\frac{\partial f(x,y)}{\partial x} , \frac{\partial f(x,y)}{\partial y}\Bigg ) \div \sqrt{ \bigg (\frac{\partial f(x,y)}{\partial x}\bigg )^2 + \bigg (\frac{\partial f(x,y)}{\partial y}\bigg )^2 } \end{split} \]

步骤如下：

  迭代 |       起点                          梯度                 位移量                  函数值 
  idx |      (x, y, ...)           (∂z/∂x,∂z/∂y,...)        (Δx,Δy,...)              z    
------+-------------------------------------------------------------------------------
    1  | (3.000000,2.000000,)  (6.000000,4.000000,)  (-0.284444,-0.189629,)  13.000000 
    2  | (2.715556,1.810371,)  (5.431104,3.620748,)  (-0.263966,-0.175978,)  10.651689 
    3  | (2.451590,1.634393,)  (4.903189,3.268781,)  (-0.244479,-0.162986,)  8.681533 
    4  | (2.207111,1.471407,)  (4.414220,2.942819,)  (-0.225956,-0.150637,)  7.036377 
    5  | (1.981155,1.320770,)  (3.962306,2.641540,)  (-0.208374,-0.138916,)  5.669409 
    6  | (1.772781,1.181854,)  (3.545564,2.363700,)  (-0.191711,-0.127807,)  4.539531 
    7  | (1.581070,1.054047,)  (3.162146,2.108096,)  (-0.175942,-0.117294,)  3.610798 
    8  | (1.405128,0.936752,)  (2.810259,1.873506,)  (-0.161043,-0.107362,)  2.851891 
    9  | (1.244085,0.829390,)  (2.488170,1.658780,)  (-0.146992,-0.097994,)  2.235636 
   10  | (1.097093,0.731396,)  (2.194187,1.462794,)  (-0.133764,-0.089176,)  1.738554 
   11  | (0.963330,0.642220,)  (1.926661,1.284439,)  (-0.121335,-0.080890,)  1.340451 
   12  | (0.841995,0.561330,)  (1.683989,1.122660,)  (-0.109682,-0.073122,)  1.024046 
   13  | (0.732312,0.488208,)  (1.464624,0.976416,)  (-0.098782,-0.065855,)  0.774629 
   14  | (0.633530,0.422354,)  (1.267061,0.844708,)  (-0.088610,-0.059073,)  0.579743 
   15  | (0.544921,0.363281,)  (1.089842,0.726561,)  (-0.079142,-0.052761,)  0.428911 
   16  | (0.465779,0.310519,)  (0.931558,0.621039,)  (-0.070354,-0.046903,)  0.313373 
   17  | (0.395425,0.263617,)  (0.790850,0.527233,)  (-0.062223,-0.041482,)  0.225855 
   18  | (0.333202,0.222134,)  (0.666403,0.444269,)  (-0.054725,-0.036483,)  0.160367 
   19  | (0.278477,0.185651,)  (0.556953,0.371302,)  (-0.047835,-0.031890,)  0.112016 
   20  | (0.230642,0.153761,)  (0.461283,0.307522,)  (-0.041530,-0.027686,)  0.076838 
   21  | (0.189112,0.126075,)  (0.378224,0.252149,)  (-0.035784,-0.023856,)  0.051658 
   22  | (0.153327,0.102218,)  (0.306655,0.204436,)  (-0.030575,-0.020383,)  0.033958 
   23  | (0.122752,0.081835,)  (0.245504,0.163669,)  (-0.025878,-0.017252,)  0.021765 
   24  | (0.096874,0.064583,)  (0.193749,0.129166,)  (-0.021668,-0.014445,)  0.013556 
   25  | (0.075207,0.050138,)  (0.150413,0.100276,)  (-0.017920,-0.011947,)  0.008170 
   26  | (0.057286,0.038191,)  (0.114573,0.076382,)  (-0.014611,-0.009741,)  0.004740 
   27  | (0.042675,0.028450,)  (0.085350,0.056900,)  (-0.011716,-0.007811,)  0.002631 
   28  | (0.030959,0.020639,)  (0.061917,0.041278,)  (-0.009210,-0.006140,)  0.001384 
   29  | (0.021749,0.014499,)  (0.043498,0.028999,)  (-0.007067,-0.004711,)  0.000683 
   30  | (0.014682,0.009788,)  (0.029364,0.019576,)  (-0.005263,-0.003509,)  0.000311 
   31  | (0.009419,0.006279,)  (0.018838,0.012559,)  (-0.003773,-0.002515,)  0.000128 
   32  | (0.005646,0.003764,)  (0.011292,0.007528,)  (-0.002570,-0.001713,)  0.000046 
   33  | (0.003076,0.002051,)  (0.006152,0.004101,)  (-0.001630,-0.001087,)  0.000014 
   34  | (0.001446,0.000964,)  (0.002892,0.001928,)  (-0.000925,-0.000617,)  0.000003 
   35  | (0.000521,0.000347,)  (0.001562,0.001389,)  (-0.000156,-0.000139,)  0.000000 
0.000521,0.000347,

最优化问题与回归性分析

优化的主要工作就是对神经网络的参数（即权重与偏置）进行拟全，让网络的输出结果与 现实的数据相吻合。

优化问题中最浅显的例子就是「回归分析」：在多变量函数中，着眼于其中一个变量， 然后用其他变量来解释这个变量。

一元线性回归分析

回归分析的种类有很多，最简单有「一元线性回归分析」。

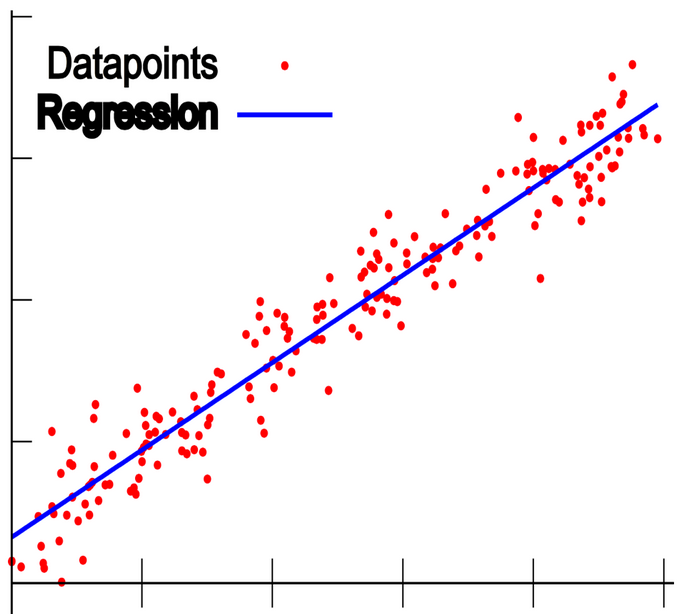
• Datapoints：离散的数据点
• Regresslon：近似地模拟离散的数据点，称为「回归直线」

多个数据点代表多个样本，从\(1\)到\(n\)：

	\(x\)	\(y\)
1	\(x_1\)	\(y_1\)
2	\(x_2\)	\(y_2\)
3	\(x_3\)	\(y_3\)
4	\(x_4\)	\(y_4\)
5	\(x_5\)	\(y_5\)
6	\(x_6\)	\(y_6\)
...	...	...
n	\(x_n\)	\(y_n\)

回归直线用公式表示：

\[ \begin{equation} y = px + q \end{equation} \label{lrt_rtsl} \]

• \(p\)为常数，称为「回归系数」
• \(q\)为常数，称为「截距」

一元线性回归分析步骤

首先收集样本：

	身高x	体重y
学生１	153.3	45.5
学生2	164.9	56.0
学生3	168.1	55.0
学生4	151.5	52.8
学生5	157.8	55.6
学生6	156.7	50.8
学生7	161.1	56.4

有了样本以后，最终目标是要示出\(px+q\)的回归系数\(p\)与截距\(q\)。现在假设回归直线 已经存在：

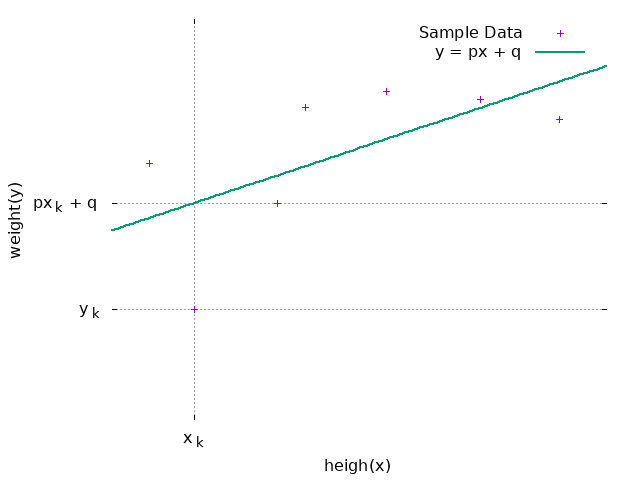
	身高x	体重y	预期值\(y=px+q\)
学生１	\(153.3\)	\(45.5\)	\(153.3p+q\)
学生2	\(164.9\)	\(56.0\)	\(164.9p+q\)
学生3	\(168.1\)	\(55.0\)	\(168.1p+q\)
学生4	\(151.5\)	\(52.8\)	\(151.5p+q\)
学生5	\(157.8\)	\(55.6\)	\(157.8p+q\)
学生6	\(156.7\)	\(50.8\)	\(156.7p+q\)
学生7	\(161.1\)	\(56.4\)	\(161.1p+q\)

对于样本中的第\(k\)位学生，实际身高为\(x_k\)，实际体重为\(y_k\)，体重预期值为：

\[ \begin{equation} px_k + q \end{equation} \label{lrt_evk} \]

实际体重\(y_k\)与预期体重的误差记为\(e_k\)：

\[ \begin{equation} e_k = y_k - (px_k + q) \end{equation} \label{lrt_eek} \]

误差\(e_k\)可能是正的也可能是负的，每个样本的正确答案\(y\)与预测值\(e\) 之间误差的平方即「平方误差」\(C_k\)：

\[ \begin{equation} C_k = (y_k - e_k)^2 \end{equation} \]

是为了方便后续的计算，平方误差乘以系数\(\frac{1}{2}\)。 理论上换成其他的系数也不会影响结果，但是\(\frac{1}{2}\)有助于以后求导方便：

\[ \begin{equation} C_k = \frac{1}{2}(y_k - e_k)^2 \end{equation} \label{lrt_ekctp} \]

把误差公式\(e_k\)在这个例子里的具体定义\ref{lrt_eek}代入平方误差公式 \ref{lrt_ekctp}后得到：

\[ \begin{equation} C_k = \frac{1}{2}(e_k)^2 = \frac{1}{2}\{y_k - (px_k + q)\}^2 \end{equation} \label{lrt_eck} \]

最小二乘法与代价函数

把所有的\(K\)个平方误差加起来，就得到代价函数（cost function），记为\(C_{\rm T}\)（T表示Total） ：

\[ \begin{equation} C_{\rm T} = C_1 + C_2 + C_3 + \cdots + C_K \end{equation} \]

\(C_{\rm T}\)所代表的误差总和有很多的名字，如：

• 「代价函数」(Cost Function)
• 「误差函数」(Error Function)
• 「损失函数」(Lost Function)

在这里我们使用代价函数这个名字，因为其他两个名字的首字母缩写容易和神经网络中 使用的词汇「熵」（Entropy）或「层」（Layer）的首字母混淆。

代价函数不止\(C_{\rm T}\)一个，根据不同的思路代价函数还有很多种其他的形式。 这里利用平方误差总和\(C_{\rm T}\)进行最优化的方法称为「最小二乘法」。

扩展到所有的数据样本，把每个样本的平方误差加起来， 把样本数据中的每一项\(y_k\)和\(px_k+q\)都代入到公式里，得到：

\[ \begin{equation} \begin{split} C_{\rm T} = & \frac{1}{2}\{45.5 - (153.3p + q)\}^2 + \frac{1}{2}\{56.0 - (164.9p + q)\}^2 + \\ & \frac{1}{2}\{55.0 - (168.1p + q)\}^2 + \frac{1}{2}\{52.8 - (151.5p + q)\}^2 + \\ & \frac{1}{2}\{55.6 - (157.8p + q)\}^2 + \frac{1}{2}\{50.8 - (156.7p + q)\}^2 + \\ & \frac{1}{2}\{56.4 - (161.1p + q)\}^2 \end{split} \end{equation} \label{lrt_ecte} \]

接下来就是要得到能使平方差最小的\(p\)与\(q\)，实现的方法是之前讲的多变量函数 最小值条件：

\[ \begin{equation} \frac{\partial C_{\rm T}}{\partial p}=0, \frac{\partial C_{\rm T}}{\partial q}=0 \end{equation} \label{lrt_ecmm} \]

代入数据：

\[ \begin{equation} \begin{split} \frac{\partial C_{\rm T}}{\partial p} = 0 = & - 153.3\{45.5 - (153.3p + q)\} - 164.9\{56.0 - (164.9p + q)\} \\ & - 168.1\{55.0 - (168.1p + q)\} - 151.5\{52.8 - (151.5p + q)\} \\ & - 157.8\{55.6 - (157.8p + q)\} - 156.7\{50.8 - (156.7p + q)\} \\ & - 161.1\{56.4 - (161.1p + q)\} \\ = & 113.4p + 7q - 372.1 \\ \frac{\partial C_{\rm T}}{\partial q} = 0 = & - \{45.5 - (153.3p + q)\} - \{56.0 - (164.9p + q)\} \\ & - \{55.0 - (168.1p + q)\} - \{52.8 - (151.5p + q)\} \\ & - \{55.6 - (157.8p + q)\} - \{50.8 - (156.7p + q)\} \\ & - \{56.4 - (161.1p + q)\} \\ = & 177312p + 113.4q - 59274 \end{split} \end{equation} \label{lrt_ected} \]

解联立方程：

\[ \begin{equation} \begin{cases} \begin{split} 113.4p + 7q & = 372.1 \\ 177312p + 113.4q & = 59274 \end{split} \end{cases} \end{equation} \label{lrt_ectedll} \]

得到：

\[ \begin{equation} p = 0.41 , q = -12.06 \end{equation} \label{lrt_ectedrs} \]

这里\(C_{\rm T}=27.86\)为最小值。把得到的\(p\)和\(q\)代入公式\ref{lrt_rtsl}， 最终回归直线的函数为：

\[ \begin{equation} y = 0.41x - 12.06 \end{equation} \label{lrt_ectedfc} \]

模型参数的个数

模型的参数个数大于数据规模，参数就不确定的。所以数据必须大于参数的个数。

习题

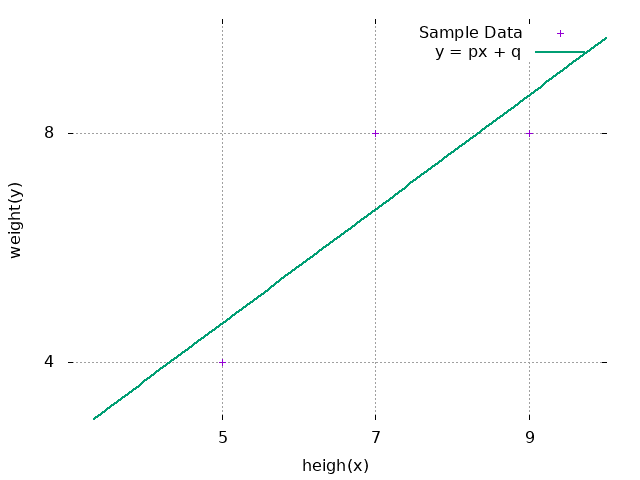
收集样本：

	数学成绩x	理科成绩y
学生1	7	8
学生2	5	4
学生3	9	8

算出预期值：

	数学成绩x	理科成绩y	预期值\(px+q\)	误差\(e=y-(px+q)\)
学生1	7	8	\(7p+q\)	\(8-(7p+q)\)
学生2	5	4	\(5p+q\)	\(4-(5p+q)\)
学生3	9	8	\(9p+q\)	\(8-(9p+q)\)

最小二乘法示平方误差：

\[ \begin{split} C_{\rm T} & = \frac{1}{2}\{8 - (7p + q)\}^2 \\ & + \frac{1}{2}\{4 - (5p + q)\}^2 \\ & + \frac{1}{2}\{8 - (9p + q)\}^2 \end{split} \]

分别求偏导：

\[ \begin{split} \frac{\partial C_{\rm T}}{\partial p} = 0 = & - 7\{8 - (7p + q)\} \\ & - 5\{4 - (5p + q)\} \\ & - 9\{8 - (9p + q)\} \\ \frac{\partial C_{\rm T}}{\partial q} = 0 = & -\{8 - (7p + q)\} \\ & -\{4 - (5p + q)\} \\ & -\{8 - (9p + q)\} \end{split} \]

解联立方程：

\[ \begin{cases} \begin{split} 21p & + 3q & = 20 \\ 155p & + 21q & = 148 \end{split} \end{cases} \]

得到：

\[ p = 1 , q = -\frac{1}{3} \]

回归直线的函数：

\[ y = x - \frac{1}{3} \]