神经网络调优

神经网络的描述

数学模型是由参数决定的。具体到神经网络中，参数包含「权重」和「偏置」。

数学模型通过调整参数使模型的输出符合实际的结果，从而确定模型， 这在数学上称为「最优化」，在神经网络中称为「学习」。

神经元模拟

接受输入

输入信号、权重与阈值

• 输入信号记为：\(x_1, x_2, \cdots , x_n\)
• 每个输入信号有对应权重（weight）记为：\(w_1, w_2, \cdots , w_n\)

\[ \begin{equation} w_1x_1 + w_2x_2 + w_3x_3 + \cdots + w_nx_n \end{equation} \label{zpt1} \]

输入要达到神经元固定的阈值（threshold）才有反应。记作：\(\theta\)。 在公式\(\ref{zpt1}\)的基础上，得到「加权输入」，用\(z\)表示：

\[ \begin{equation} z = w_1x_1 + w_2x_2 + w_3x_3 + \cdots + w_nx_n - \theta \end{equation} \label{zpt2} \]

优化输入公式

在公式\(\ref{zpt2}\)中，只有阈值一项是减法，为了公式看起来整齐， 设\(b=-\theta\)，得到：

\[ \begin{equation} z = w_1x_1 + w_2x_2 + w_3x_3 + \cdots + w_nx_n + b \end{equation} \label{zpt3} \]

公式\(\ref{zpt3}\)里每个信号都要乘以权重，为了整齐给\(b\)乘以权重\(1\)：

\[ \begin{equation} z = w_1x_1 + w_2x_2 + w_3x_3 + \cdots + w_nx_n + 1 \times b \end{equation} \label{zpt_fin} \]

公式\(\ref{zpt_fin}\)与公式\(\ref{zpt2}\)相比可不仅仅是样子好看。 它还可以进一步转为两个向量的内积：

\[ \begin{equation} z = (x_1, x_2, x_3 \cdots x_n, 1) (w_1, w_2, w_3 \cdots w_n, b) \end{equation} \label{zpt_vct} \]

内积运算更加便于计算机处理。

激活函数

加权输入\(z\)作为参数传入激活函数（activation function）记作\(a\)，得到输出结果\(y\)：

\[ \begin{equation} y = a(w_1x_1 + w_2x_2 + \cdots + w_nx_n - \theta) = a(z) \end{equation} \label{zpt_a1} \]

例举常用的四种激活函数：

• S函数（Sigmoid）记作\(\sigma(z)\)，值域在0到1之间，连续可导。
• 双切反曲函数（hyperbolic tangent）。
• 阈值函数（Hard limiting threshold）也叫单位阶跃函数，记作\(U(z)\)。
• 纯线性函数（Purely linear）。

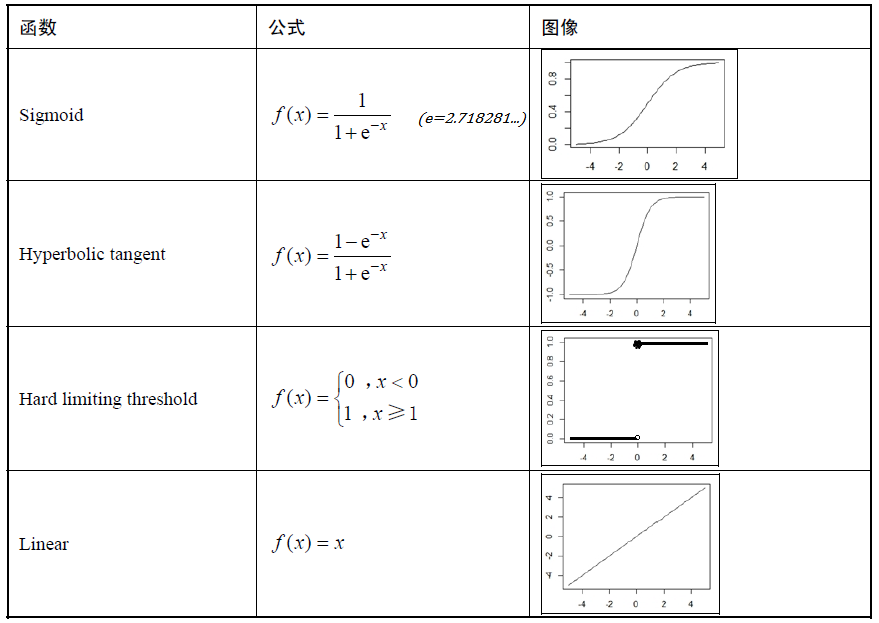
这里选用Sigmoid函数：

\[ \begin{equation} \sigma(x) = \frac{1}{1 + {\rm e}^{-x}} = \frac{1}{1+{\rm exp}(-x)} \quad \quad ({\rm e}=2.71828 \cdots) \end{equation} \label{fc_sgmd2} \]

优点：

• 对所有输入有定义
• 输出范围固定：\((0, 1)\)
• 连续、可导（而且求导方便）

求导：

\[ \begin{equation} \begin{split} \sigma ' (x) &= (\frac{1}{1 + e^{-x}})' = \frac{(1 + e^{-x})' }{(1 + e^{-x})^2} = \frac{e^{-x} }{(1 + e^{-x})^2} \\ &= \frac{1 + e^{-x}-1 }{(1 + e^{-x})^2} = \frac{1+e^{-x}}{ (1+e^{-x})^2} - \frac{1}{(1+e^{-x })^2} \\ &= \frac{1}{1+e^{-x}} - \frac{1}{(1+e^{-x })^2} \\ &= \sigma(x) - \sigma(x)^2 \\ &= \sigma(x)(1 - \sigma(x)) \end{split} \end{equation} \label{pf_sigmoid2} \]

组成网络

把多个神经单元连接成网络状，就成了「神经网络」。比如基础的「阶层型神经网络」 和由其发展而来的「卷积神经网络」。

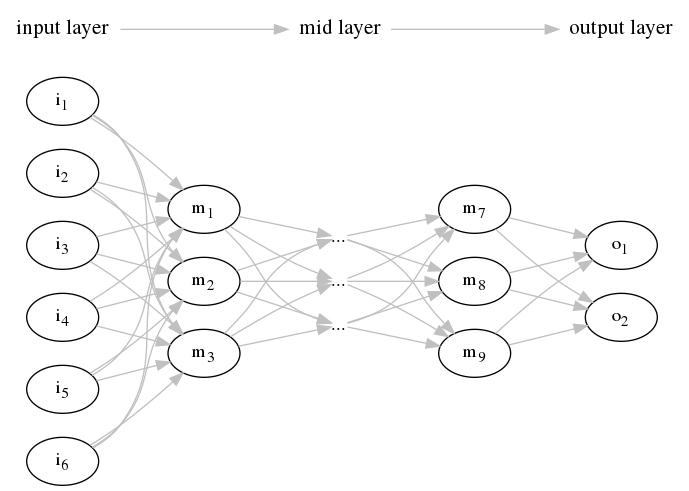
• 「输入层」负责读取输入的信息，仅仅把值原样输出到一下层。
• 「隐藏层」也叫「中间层」，负责主要的计算工作。
• 「输出层」不仅和隐藏层一样执行计算工作，还会输出计算结果。

如果前一层的神经单元与下一层的所有神经单元都有箭头连接，这样的层构造称为 「全连接层」（fully connected layer）。

输入层

输入层的神经单元与位图的像素完全一一对应，而且输入与输出完全相等。 可以省略激活函数或者直接把恒等式作为激活函数：

\[ \begin{equation} a(z) = z \end{equation} \label{fc_raw} \]

神经网络中的变量与参数

对于神经网络中的第\(j\)个神经元加权\(z_j\)的描述公式：

\[ z_j = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b \]

通过激活函数\(a()\)得到输出：

\[ a_j = a(z_j) = a(w_1x_1 + w_2x_2 + \cdots + w_nx_n + b) \]

• 变量：\(z_j\)、\(a_j\)、\(x_1\)到\(x_n\)
• 参数：偏置\(b\)、权重\(w_1\)到\(w_n\)

表示位置

神经元的位置用所在的层数加上位于层是的位置表示：

• 上标\(l\)用来表示层数。
• 下标\(j\)用来表示层中的位置。

表示变量与参数的方法

• 标记「神经元（或输出）」用字母\(a\)。例如，第\(l\)层的第\(j\)个神经元与它的输出记为： \(a^l_j\)
• 标记神经元的「加权」用字母\(z\)。例如，第\(l\)层的第\(j\)个神经元的加权，记为：\(z^l_j\)
• 标记神经元的「偏置」用字母\(b\)。例如，第\(l\)层的第\(j\)个神经元的偏置，记为：\(b^l_j\)

每个神经元有多个输入和与之对应的权重，因为输入一定是来自于它的前一层 （即\(l-1\)层），所以要用下标\(i\)标明输入是从前一层的哪一个神经元输出的。

• 标记神经元的「输入」用字母\(x\)。例如，第\(l\)层的第\(j\)个神经元来自于前一层第\(i\) 个神经元的输入，记为：\(x^l_{j,i}\)
• 标记神经元的「输入权重」用字母\(w\)。例如，第\(l\)层的第\(j\)个神经元来自于前一层第 \(i\)个神经元的输入的权重，记为：\(w^l_{j,i}\)

表示变量值的方法

变量的值是由输入样本来决定的。以第\(l\)层第\(j\)个神经元对例，对于第\(k\)个样本：

• 从前一层第\(i\)个「输入」： \(x^l_{j,i}[k]\)
• 「加权输入」：\(z^l_j[k]\)
• 「输出」：\(a^l_j[k]\)

回到位图0和1的例子，我们有很多图片作为为样本，其中第7张图片是这个样子的：

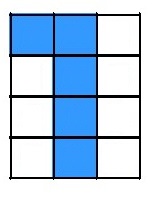
对于中间层的\(a^2_1\)、\(a^2_2\)、\(a^2_3\)从输入层得到的变量\(x_1\)到\(x_{12}\)值都为：

\[ \begin{split} x_1[7] & = 1, x_2[7] & = 1, x_3[7] & = 0, x_4[7] & = 0, \\ x_5[7] & = 1, x_6[7] & = 0, x_7[7] & = 0, x_8[7] & = 1, \\ x_9[7] & = 0, x_{10}[7] & = 0, x_{11}[7] & = 1, x_{12}[7] & = 0 \end{split} \]

以\(z^2_1\)为例，代主所有变量\(x\)时，要注意权重\(w\)与偏置\(b\)是常量，不会因为样本的变化而改变的：

\[ \begin{split} z^2_1[7] = & w^2_{1,1} \times 1 + w^2_{1,2} \times 1 & + w^2_{1,3} \times 0 & + w^2_{1,4} \times 0 & + \\ & w^2_{1,5} \times 1 + w^2_{1,6} \times 0 & + w^2_{1,7} \times 0 & + w^2_{1,8} \times 1 & + \\ & w^2_{1,9} \times 0 + w^2_{1,10} \times 0 & + w^2_{1,11} \times 1 & + w^2_{1,12} \times 0 & + b^2_1 \end{split} \]

得到：

\[ \begin{split} z^2_1[7] = w^2_{1,1} + w^2_{1,2} + w^2_{1,5} + w^2_{1,8} + w^2_{1,11} + b^2_1 \end{split} \]

用符号表示神经网络

如下形式用来表示神经元之间的关系：

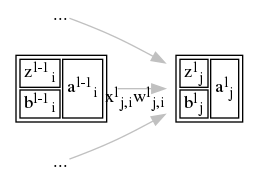
神经网络的变量的关系式

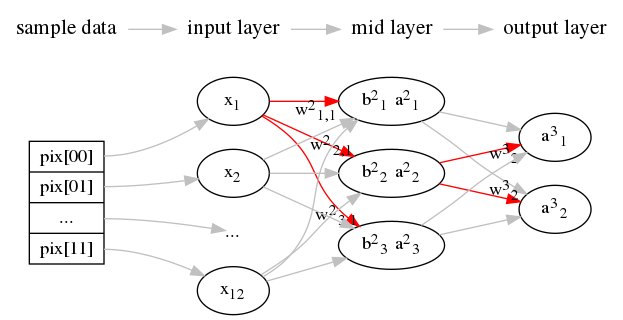
输入层的关系式

输入层是第一层，一般直接省略层数1用\(x_i\)表示：

\[ \begin{equation} a^l_i = x_i \end{equation} \label{vblat_iptlar} \]

隐藏层的关系式

设激活函数的\(a(z)\)，则中间层的变量与参数的关系为：

\[ \begin{equation} \begin{cases} a^2_1 = a(z^2_1) = a(w^2_{1,1} \cdot x_1 + w^2_{1,2} \cdot x_2 + \cdots + w^2_{1,12} \cdot x_{12} + b^2_1) \\ a^2_2 = a(z^2_2) = a(w^2_{2,1} \cdot x_1 + w^2_{2,2} \cdot x_2 + \cdots + w^2_{2,12} \cdot x_{12} + b^2_2) \\ a^2_3 = a(z^2_3) = a(w^2_{3,1} \cdot x_1 + w^2_{3,2} \cdot x_2 + \cdots + w^2_{3,12} \cdot x_{12} + b^2_3) \end{cases} \end{equation} \label{vblat_midlr} \]

其中\(z\)在计算机中以矩阵的方式处理为：

\[ \begin{equation} \begin{pmatrix} z^2_1 \\ z^2_2 \\ z^2_3 \end{pmatrix} \label{vblat_midlrmtx} = \begin{pmatrix} w^2_{1,1} & w^2_{1,2} & \cdots & w^2_{1,12} \\ w^2_{2,1} & w^2_{2,2} & \cdots & w^2_{2,12} \\ w^2_{3,1} & w^2_{3,2} & \cdots & w^2_{3,12} \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ \cdots \\ x_{12} \end{pmatrix} + \begin{pmatrix} b^2_1 \\ b^2_2 \\ b^2_3 \end{pmatrix} \end{equation} \]

更一般化表示，当前层为第\(l\)层，一共有\(J\)个神经元，前一层有\(I\)个神经元：

\[ \begin{equation} \begin{cases} a^l_1 &= a(z^l_1) = a(w^l_{1,1} \cdot x_1 + w^l_{1,2} \cdot x_2 + \cdots + w^l_{1,i} \cdot x_{i} + \cdots + w^l_{1,I} \cdot x_{I} + b^l_1) \\ a^l_2 &= a(z^l_2) = a(w^l_{2,1} \cdot x_1 + w^l_{2,2} \cdot x_2 + \cdots + w^l_{2,i} \cdot x_{i} + \cdots + w^l_{2,I} \cdot x_{I} + b^l_2) \\ & \vdots \\ a^l_j &= a(z^l_j) = a(w^l_{j,1} \cdot x_1 + w^l_{j,2} \cdot x_2 + \cdots + w^l_{j,i} \cdot x_{i} + \cdots + w^l_{j,I} \cdot x_{I} + b^l_j) \\ & \vdots \\ a^l_J &= a(z^l_J) = a(w^l_{J,1} \cdot x_1 + w^l_{J,2} \cdot x_2 + \cdots + w^l_{J,i} \cdot x_{i} + \cdots + w^l_{J,I} \cdot x_{I} + b^l_J) \end{cases} \end{equation} \label{vblat_midlr_jnl} \] \[ \begin{equation} \begin{pmatrix} z^l_1 \\ z^l_2 \\ \vdots \\ z^l_j \\ \vdots \\ z^l_J \end{pmatrix} = \begin{pmatrix} w^l_{1,1} & w^l_{1,2} & \cdots & w^l_{1,i} & \cdots & w^l_{1,I} \\ w^l_{2,1} & w^l_{2,2} & \cdots & w^l_{2,i} & \cdots & w^l_{2,I} \\ \vdots \\ w^l_{j,1} & w^l_{j,2} & \cdots & w^l_{j,i} & \cdots & w^l_{j,I} \\ \vdots \\ w^l_{J,1} & w^l_{J,2} & \cdots & w^l_{J,i} & \cdots & w^l_{J,I} \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_i \\ \vdots \\ x_{I} \end{pmatrix} + \begin{pmatrix} b^l_1 \\ b^l_2 \\ \vdots \\ b^l_j \\ \vdots \\ b^l_J \end{pmatrix} \end{equation} \label{vblat_midlrmtx_jnl} \]

输出层的关系式

输出层的变量与参数关系和公式\(\ref{vblat_midlr}\)一样，把对应的本层与上一层值代入：

\[ \begin{equation} \begin{cases} a^3_1 = a(z^3_1) = a(w^3_{1,1} \cdot a^2_1 + w^3_{1,2} \cdot a^2_2 + w^3_{1,3} \cdot a^2_3 + b^3_1) \\ a^3_2 = a(z^3_2) = a(w^3_{2,1} \cdot a^2_1 + w^3_{2,2} \cdot a^2_2 + w^3_{2,3} \cdot a^2_3 + b^3_2) \end{cases} \end{equation} \label{vblat_outptlr} \]

其中\(z\)同样可以用矩阵表示：

\[ \begin{equation} \begin{pmatrix} z^3_1 \\ z^3_2 \end{pmatrix} = \begin{pmatrix} w^3_{1,1} & w^3_{1,2} & w^3_{1,3} \\ w^3_{2,1} & w^3_{2,2} & w^3_{2,3} \end{pmatrix} \cdot \begin{pmatrix} a^2_1 \\ a^2_2 \\ a^2_3 \end{pmatrix} + \begin{pmatrix} b^3_1 \\ b^3_2 \end{pmatrix} \end{equation} \label{vblat_outptlrmtx} \]

更一般化表示，输出层为第\(L\)层，一共有\(J\)个神经元，前一层有\(I\)个神经元：

\[ \begin{equation} \begin{cases} a^L_1 = a(z^L_1) = a(w^L_{1,1} \cdot a^{L-1}_1 + w^L_{1,2} \cdot a^{L-1}_2 + \cdots + w^L_{1,i} \cdot a^{L-1}_i + \cdots + w^L_{1,I} \cdot a^{L-1}_I + b^L_1) \\ a^L_2 = a(z^L_2) = a(w^L_{2,1} \cdot a^{L-1}_1 + w^L_{2,2} \cdot a^{L-1}_2 + \cdots + w^L_{2,i} \cdot a^{L-1}_i + \cdots + w^L_{2,I} \cdot a^{L-1}_I + b^L_2) \\ \vdots \\ a^L_j = a(z^L_j) = a(w^L_{j,1} \cdot a^{L-1}_1 + w^L_{j,2} \cdot a^{L-1}_2 + \cdots + w^L_{j,i} \cdot a^{L-1}_i + \cdots + w^L_{j,I} \cdot a^{L-1}_I + b^L_j) \\ \vdots \\ a^L_J = a(z^L_J) = a(w^L_{J,1} \cdot a^{L-1}_1 + w^L_{J,2} \cdot a^{L-1}_2 + \cdots + w^L_{J,i} \cdot a^{L-1}_i + \cdots + w^L_{J,I} \cdot a^{L-1}_I + b^L_J) \end{cases} \end{equation} \label{vblat_outptlr_jnl} \] \[ \begin{equation} \begin{pmatrix} z^L_1 \\ z^L_2 \\ \vdots \\ z^L_j \\ \vdots \\ z^L_J \end{pmatrix} = \begin{pmatrix} w^L_{1,1} & w^L_{1,2} & \cdots & w^L_{1,i} & \cdots & w^L_{1,I} \\ w^L_{2,1} & w^L_{2,2} & \cdots & w^L_{2,i} & \cdots & w^L_{2,I} \\ \vdots \\ w^L_{j,1} & w^L_{j,2} & \cdots & w^L_{j,i} & \cdots & w^L_{j,I} \\ \vdots \\ w^L_{J,1} & w^L_{J,2} & \cdots & w^L_{J,i} & \cdots & w^L_{J,I} \end{pmatrix} \cdot \begin{pmatrix} a^{L-1}_1 \\ a^{L-1}_2 \\ \vdots \\ a^{L-1}_i \\ \vdots \\ a^{L-1}_I \end{pmatrix} + \begin{pmatrix} b^L_1 \\ b^L_2 \\ \vdots \\ b^L_j \\ \vdots \\ b^L_J \end{pmatrix} \end{equation} \label{vblat_outptlrmtx_jnl} \]

神经网络的调优

学习数据和正解

正解是每个样本正确的解，是用来帮助训练神经网络的。

如何表示正确的解

回到数字识别的例子：

第三层是输出层，两个神经元\(a^3_1\)和\(a^3_2\)分别代表结果为\(0\)与结果为\(1\)：

	期望输出
	图像为0	图像为1
\(a^3_1\)	接近1	接近0
\(a^3_2\)	接近0	接近1

那么对于以下的样本：

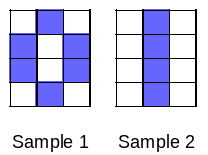
分别用\(t_1\)和\(t_2\)来表示对于每个样本，\(a^3_1\)和\(a^3_2\)正确的输出：

	含义	图像为0时	图像为1时
\(t_1\)	\(a^3_1\)的正确输出	1	0
\(t_2\)	\(a^3_2\)的正确输出	0	1

因为\(t_1\)和\(t_2\)对应到\(a^3_1\)和\(a^3_2\)的预期值，所以神经网络的正解可以用 预期值和正解的平方误差\(C\)来表示：

\[ \begin{equation} C = \frac{1}{2}\{(t_1-a^3_1)^2 + (t_2-a^3_2)^2\} \end{equation} \label{vblat_epta} \]

以上公式\ref{vblat_epta}更加一般化到层数为\(L\)层的神经网络中， 第\(L\)层输出层共有\(I\)个输出单元的网络中的公式：

\[ \begin{equation} C = \frac{1}{2}\{(t_1-a^L_1)^2 + (t_2-a^L_2)^2 + \cdots + (t_i-a^L_i)^2 + \cdots + (t_I-a^L_I)^2\} \end{equation} \label{vblat_epta1} \]

其中\(\frac{1}{2}\)只是为了求导时计算方便，不影响最终结果。

以上公式\(\ref{vblat_epta}\)看起来不复杂，但是实际应用中收敛较慢。实际应用的其他 误差指标很多，比较有名指标是从信息论中熵概念派生的「交叉熵」指标：

\[ \begin{equation} - \frac{1}{n}\{ [t_1\log{}a_1 + (1-t_1)\log(1-a_1)] + [t_2\log{}a_2 + (1-t_2)\log(1-a_2)] \} \end{equation} \label{vblat_xepc} \]

其中\(n\)代表数据规模。利用上面的公式\(\ref{vblat_xepc}\)和Sigmoid函数， 可以消除sigmoid函数的冗长性，提高梯度下降法的计算速度。

神经网络的代价函数

模型参数的表示总体误差的函数称为「代价函数」，也叫「误差函数」、「损失函数」 、「目的函数等」。

求出代价函数

平方误差公式\(\ref{vblat_epta}\)为基础，应用到64个样本上， 其中第\(k\)个样本的误差为：

\[ \begin{equation} C_k = - \frac{1}{2}\{ (t_1[k] -a^3_1[k])^2 + (t_2[k] -a^3_2[k])^2 \} \end{equation} \label{vblat_eptaexpstp1} \]

\(n\)个样本全加起来，就是代价函数\(C_{\rm T}\)：

\[ \begin{equation} C_{\rm T} = C_1 + C_2 + \cdots + C_{n} \end{equation} \label{vblat_eptaexpstpw} \]

具体到例子里就是64个样本：

1. 要把隐藏层的公式\ref{vblat_midlr}代入输出层的公式\ref{vblat_outptlr}
2. 再把输出层的公式\ref{vblat_outptlr}代入平方误差\ref{vblat_epta}
3. 再把64个样本分别代入平方误差\ref{vblat_epta}得到每个样本的平方误差\ref{vblat_eptaexpstp1}
4. 最后把64个样本的平方误差代入代价函数\ref{vblat_eptaexpstpw}

求出参数的个数和标本的规模

把梯度应用到神经网络中，以一个12:3:2的全连接网络为例子， 第\(k\)个样本到第三层输出层的「平方误差」\(C_k\)公式\ref{vblat_eptaexpstp1} 与「代价函数」\(C_{\rm T}\)公式\ref{vblat_eptaexpstpw} 。

参数的个数的数据规模：

• 隐藏层有3个神经元，每个神经元要一个偏置和12个输入权重，一共是\(3\)个偏置和\(36\)个权重。
• 输出层有2个神经元，每个神经元要一个偏置和3个输入权重，一共是\(2\)个偏置和\(6\)个权重。

所以参数的个数有：

\[ \begin{equation} (12 \times 3 + 3) + (3 \times 2 + 2) = 47 \end{equation} \label{vbca_pmc} \]

根据公式\ref{vbca_pmc}的计算最终要确定的参数（权重和偏置）一共有47个， 所以样本的数量至少要47张，不然不够解联立方程组。

神经网络与回归性分析的差异

• 神经网络中参数的数目大得多。
• 线性回归分析中使用的函数为一次式；神经网络中使用的激活函数不是一次式，要更加复杂。

由于这两点差异，可以联想到：

以之前求出的代价函数\(\ref{vblat_eptaexpstpw}\)为例，无法用参数（权重与偏置） 的式子把代价函数表示出，就算非要写出来也是无比复杂的； 就算不嫌函数复杂，下一步还要进行求导； 而且由于引入了激活函数的导数，就算求导求出来了，结果也不会很漂亮。

所以，相比回归分析，神经网络需要更加强大的数学工具，例如「误差反向传播法」。

神经网络中的梯度下降

对于光滑的函数\(f(x_1,x_2,\cdots,x_n)\)，如果每个变量做出微小的变化：

\[ \begin{equation} x_1+\Delta x_1 , x_2+\Delta x_2 , \cdots x_n+\Delta x_n \end{equation} \label{nnw_ffpm} \]

则当满足以下关系，函数\(f\)减少的速度最快（\(\eta\)为正的微小常量）：

\[ \begin{equation} (\Delta x_1 , \Delta x_2 , \cdots , \Delta x_n) = - \eta \Bigg ( \frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2} , \cdots , \frac{\partial f}{\partial x_n } \Bigg ) \quad \quad (\eta\text{为正的微小常量}) \end{equation} \label{nnw_fftd} \]

公式\ref{nnw_fftd}中\(\big ( \frac{\partial f}{\partial x_1} , \frac{\partial f}{\partial x_2} , \cdots , \frac{\partial f}{\partial x_n } \big )\) 就是函数\(f\)的「梯度」。应用到例子中就是：

\[ \begin{equation} (\Delta w^2_{1,1}, \cdots , \Delta w^3_{2,3}, \Delta b^2_1, \cdots , \Delta b^3_2) = - \eta \Bigg ( \frac{\partial C_{\rm T}}{\partial w^2_{1,1}}, \cdots , \frac{\partial C_{\rm T}}{\partial w^3_{2,3}}, \frac{\partial C_{\rm T}}{\partial b^2_1}, \cdots , \frac{\partial C_{\rm T}}{\partial b^3_2} \Bigg ) \end{equation} \label{nnw_ffte} \]

下降的最短路径就是从\((w^2_{1,1}, \cdots, b^2_1 \cdots)\)移动到 \((w^2_{1,1} + \Delta w^2_{1,1}, \cdots, b^2_1 + \Delta b^2_1, \cdots)\) 然后把这一个位置再作为下一轮梯度下降的起点。

关于分量的偏导

因为这个神经网络的例子的表达式\ref{vblat_midlr}和\ref{vblat_outptlr}里有47个参数 （权重和偏置），那么公式\ref{nnw_ffte}所表达的梯度也有47个「分量」。 如果要用偏导为0求最小值的方式来，那就至少要解47个方程：

\[ \begin{equation} \frac{\partial C_{\rm T}}{\partial w^2_{1,1}} = 0, \quad \cdots , \quad \frac{\partial C_{\rm T}}{\partial w^3_{2,3}} = 0, \quad \quad \quad \frac{\partial C_{\rm T}}{\partial b^2_1} = 0, \quad \cdots , \quad \frac{\partial C_{\rm T}}{\partial b^3_2} = 0 \end{equation} \label{nnw_ffct} \]

以其中一个参数\(w^2_{1,1}\)为例，在第\(k\)个样本时平方差\(C_k\)对于 \(w^2_{1,1}\)的偏导为\(\frac{\partial C_k}{\partial w^2_{1,1}}\)， 然后再根据偏导数的链式法则进行如下变形：

\[ \begin{equation} \begin{split} \frac{\partial C_k}{\partial w^2_{1,1}} = & \frac{\partial C_k}{\partial a^3_1[k]} \cdot \frac{\partial a^3_1[k]}{\partial z^3_1[k]} \cdot \frac{\partial z^3_1[k]}{\partial a^2_1[k]} \cdot \frac{\partial a^2_1[k]}{\partial z^2_1[k]} \cdot \frac{\partial z^2_1[k]}{\partial w^2_{1,1}} + \\ & \frac{\partial C_k}{\partial a^3_2[k]} \cdot \frac{\partial a^3_2[k]}{\partial z^3_2[k]} \cdot \frac{\partial z^3_2[k]}{\partial a^2_1[k]} \cdot \frac{\partial a^2_1[k]}{\partial z^2_1[k]} \cdot \frac{\partial z^2_1[k]}{\partial w^2_{1,1}} \end{split} \end{equation} \label{nnw_chtfs} \]

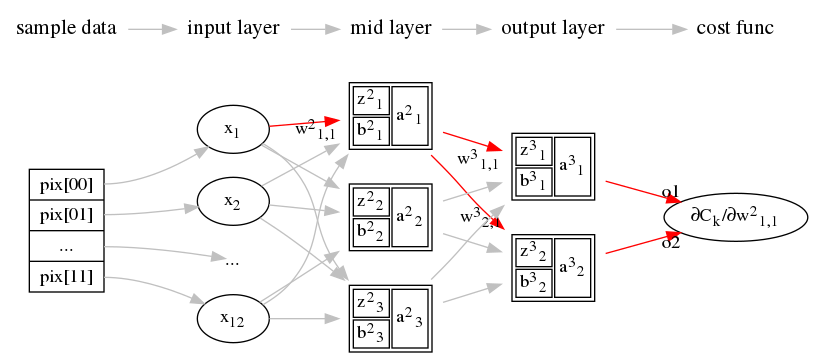
整个代价函数\(C_{\rm T}\)关于\(w^2_{1,1}\)这个分量的偏导为 \(\frac{\partial C_{\rm T}}{\partial w^2_{1,1}}\)（即公式\(\ref{nnw_chtfs}\)） 代入到代价函数\(C_{\rm T}\)中得到：

\[ \begin{equation} \begin{split} \frac{\partial C_{\rm T}}{\partial w^2_{1,1}} = & \frac{\partial C_1 }{\partial w^2_{1,1}} + \frac{\partial C_2 }{\partial w^2_{1,1}} + \cdots + \frac{\partial C_{64}}{\partial w^2_{1,1}} \\ = & \Bigg ( \frac{\partial C_1}{\partial a^3_1[1]} \cdot \frac{\partial a^3_1[1]}{\partial z^3_1[1]} \cdot \frac{\partial z^3_1[1]}{\partial a^2_1[1]} \cdot \frac{\partial a^2_1[1]}{\partial z^2_1[1]} \cdot \frac{\partial z^2_1[1]}{\partial w^2_{1,1}} + \\ & \frac{\partial C_1}{\partial a^3_2[1]} \cdot \frac{\partial a^3_2[1]}{\partial z^3_2[1]} \cdot \frac{\partial z^3_2[1]}{\partial a^2_1[1]} \cdot \frac{\partial a^2_1[1]}{\partial z^2_1[1]} \cdot \frac{\partial z^2_1[1]}{\partial w^2_{1,1}} \Bigg ) \\ & + \cdots + \\ & \Bigg ( \frac{\partial C_{64}}{\partial a^3_1[64]} \cdot \frac{\partial a^3_1[64]}{\partial z^3_1[64]} \cdot \frac{\partial z^3_1[64]}{\partial a^2_1[64]} \cdot \frac{\partial a^2_1[64]}{\partial z^2_1[64]} \cdot \frac{\partial z^2_1[64]}{\partial w^2_{1,1}} + \\ & \frac{\partial C_64}{\partial a^3_2[64]} \cdot \frac{\partial a^3_2[64]}{\partial z^3_2[64]} \cdot \frac{\partial z^3_2[64]}{\partial a^2_1[64]} \cdot \frac{\partial a^2_1[64]}{\partial z^2_1[64]} \cdot \frac{\partial z^2_1[64]}{\partial w^2_{1,1}} \Bigg ) \end{split} \end{equation} \label{nnw_chtct} \]

先求导再求和

为了求得代价函数\(C_{\rm T}\)的梯度下降基本式\ref{nnw_ffte}中的各个梯度分量， 可以先求公式\ref{vblat_epta}的平方误差\(C\)的偏导数，最后对全体学习数据求和即可。 逻辑上需要求64次偏导，这样只要求1次偏导就可以了。

神经单元误差\(\delta\)

定义新的概念「神经元误差」（error）\(\delta^l_j\)：

\[ \begin{equation} \delta^l_j = \frac{\partial C}{\partial z^l_j} \quad (l=2,3,\cdots) \end{equation} \label{nnw_nnernd} \]

注意：神经单元误差\(\delta\)与平方误差\(C\)是不同的概念。 \(\delta^l_j\)表示某个神经单元（\(a^l_j\)）的加权输入\(z^l_j\)给平方误差\(C\) 带来的变化率。如果神经网络符合数据，神经元误差\(\delta^l_j\)也一定为\(0\)。

例，用神经元误差来表示参数\(z^2_1\)与\(z^3_2\)：

\[ \begin{equation} \delta^2_1 = \frac{\partial C}{\partial z^2_1} \quad , \quad \delta^3_2 = \frac{\partial C}{\partial z^3_2} \end{equation} \]

用神经元误差\(\delta\)表示平方误差\(C\)中关于权重、偏置的偏导数

用\(\delta^l_j\)表示\(\frac{\partial C}{\partial w^2_{1,1}}\)，可以先用链式法则得到:

\[ \begin{equation} \frac{\partial C}{\partial w^2_{1,1}} = \frac{\partial C}{\partial z^2_1} \cdot \frac{\partial z^2_1}{\partial w^2_{1,1}} \end{equation} \label{csoe_nt2} \]

根据\(z^2_1\)的定义：

\[ \begin{equation} \frac{\partial z^2_1}{\partial w^2_{1,1}} = \frac{\partial (w^2_{1,1}x_1 + w^2_{1,2}x_2 + \cdots + w^2_{1,12}x_{12} + b^2_1)}{\partial w^2_{1,1}} = x_1 \end{equation} \label{csoe_nt3} \]

把神经单元误差\ref{nnw_nnernd}和公式\ref{csoe_nt3}代入式子\ref{csoe_nt2}， 得到：

\[ \begin{equation} \frac{\partial C}{\partial w^2_{1,1}} = \delta^2_1 \cdot x_1 \end{equation} \label{csoe_nt4} \]

而对于第一层，因为输入与输出相同，所以\(x_1=a^1_1\)，得到：

\[ \begin{equation} \frac{\partial C}{\partial w^2_{1,1}} = \delta^2_1 \cdot a^1_1 \end{equation} \label{csoe_nt5} \]

总结一下：

\[ \begin{equation} \frac{\partial C}{\partial w^2_{1,1}} = \frac{\partial C}{\partial z^2_1} \cdot \frac{\partial z^2_1}{\partial w^2_{1,1}} = \delta^2_1 \cdot \frac{\partial (w^2_{1,1}a^1_1 + w^2_{1,2}a^1_2 + \cdots + w^2_{1,12}a^1_{12} + b^2_1)}{\partial w^2_{1,1}} = \delta^2_1 \cdot a^1_1 \end{equation} \]

同理对于\(\frac{\partial C}{\partial w^3_{1,1}}\)可以表示为：

\[ \begin{equation} \frac{\partial C}{\partial w^3_{1,1}} = \frac{\partial C}{\partial z^3_1} \cdot \frac{\partial z^3_1}{\partial w^3_{1,1}} = \delta^3_1 \cdot \frac{\partial (w^3_{1,1}a^2_1 + w^3_{1,2}a^2_2 + w^3_{1,3}a^2_3 + b^3_1)}{\partial w^3_{1,1}} = \delta^3_1 \cdot a^2_1 \end{equation} \]

同理对于偏置\(\frac{\partial C}{\partial b^2_1}\)、\(\frac{\partial C}{\partial b^3_1}\) 可以表示为：

\[ \begin{equation} \frac{\partial C}{\partial b^2_1} = \frac{\partial C}{\partial z^2_1} \frac{\partial z^2_1}{\partial b^2_1} = \delta^2_1 \frac{\partial (w^2_{1,1}a^1_1 + w^2_{1,2}a^1_2 + \cdots + w^2_{1,12}a^1_{12} + b^2_1)}{\partial b^2_1} = \delta^2_1 \cdot 1 = \delta^2_1 \end{equation} \] \[ \begin{equation} \frac{\partial C}{\partial b^3_1} = \frac{\partial C}{\partial z^3_1} \frac{\partial z^3_1}{\partial b^3_1} = \delta^3_1 \frac{\partial (w^3_{1,1}a^2_1 + w^3_{1,2}a^2_2 + w^3_{1,3}a^2_3 + b^3_1)}{\partial b^3_1} = \delta^3_1 \cdot 1 = \delta^3_1 \end{equation} \]

可以总结出权重与偏置的一般公式，就把\(\delta\)与\(C\)关于权重和偏置的偏导数联系起来了：

\[ \begin{equation} \frac{\partial C}{\partial w^l_{j,i}} = \delta^l_i \cdot a^{l-1}_i , \quad \frac{\partial C}{\partial b^l_j} = \delta^l_i \quad (l=2,3,\cdots) \end{equation} \label{csoe_genfm} \]

如果能求出\(\delta^l_j\)，就可以根据公式\ref{csoe_genfm}求出平方误差公式\(C\)的偏导。 然后对于全体数据，把公式\ref{csoe_genfm}相加，从而计算出代价函数\(C_{\rm T}\)的梯度。

误差反向传播法

要寻找多变量函数的最小值，梯度下降法是非常有用的； 但是神经网络中不能直接使用梯度下降法，要借助「误差反向传播法」（BP）。 神经单元误差\(\delta^l_j\)的递推关系式\ref{csoe_genfm}可以用来避开复杂的导数计算。

计算输出层的\(\delta^l_j\)

在一个数列中第一项为首项，最后一项为末项。 如果把神经单元误差公式\ref{nnw_nnernd}看作一个数列\({\delta^l_j}\)， 可以简单地求出它的末项，就是输出层的神经单元误差\(\delta^3_j,(j=1,2)\)。 以\(a(z)\)为激活函数，根据链式法则，有：

\[ \begin{equation} \delta^3_j=\frac{\partial C}{\partial z^3_j}= \frac{\partial C}{\partial a^3_j} \cdot \frac{\partial a^3_j}{\partial z^3_j}= \frac{\partial C}{\partial a^3_j} \cdot a'(z^3_j) \end{equation} \label{cose_bpsp} \]

要列出所有的\(\delta^3_1\)、\(\delta^3_2\)，可以用矩阵表示更加清楚：

\[ \begin{equation} \begin{pmatrix} \delta^3_1 \\ \delta^3_2 \\ \end{pmatrix} = \begin{pmatrix} \frac{\partial C}{\partial a^3_1} \\ \frac{\partial C}{\partial a^3_2} \\ \end{pmatrix} \odot \begin{pmatrix} a'(z^3_1) \\ a'(z^3_2) \\ \end{pmatrix} \end{equation} \label{cose_bpsp2} \]

这样，如果给出平方误差\(C\)和激活激活函数\(a()\)，就可以得到输出层神经单元的误差 \(\delta^3_j\)。以\(L\)特指输出层的编号，那么\ref{cose_bpsp} 可以一般化为输出层的神经单元误差公式：

\[ \begin{equation} \delta^L_j = \frac{\partial C}{\partial a^L_j} \cdot a'(z^L_j) \end{equation} \label{cose_bpgnl} \]

例，实际计算\(\delta^3_1\)。根据平方误差公式\ref{vblat_epta}：

\[ \begin{equation} C = \frac{1}{2}\{(t_1-a^3_1)^2 + (t_2-a^3_2)^2\} = \frac{1}{2}\{(a^3_1 - t_1)^2 + (a^3_2 - t_2)^2\} \end{equation} \label{cose_bpcp10} \]

在这个表达式基础上，对\(a^3_1\)求偏导可以得到：

\[ \begin{equation} \frac{\partial C}{\partial a^3_1} = a^3_1 - t1 \end{equation} \label{cose_bpcp11} \]

以\(L\)特指输出层的编号，那么上面公式可以一般化为：

\[ \begin{equation} \frac{\partial C_k}{\partial a^L_j} = a^L_j[k] - t_j[k] \end{equation} \label{cose_bpcp11g} \]

把上面式\ref{cose_bpcp10}与式\ref{cose_bpcp11g}代入上面的式\ref{cose_bpgnl}：

\[ \begin{equation} \delta^3_1 = (a^3_1 - t_1) \cdot a'(z^3_1) \end{equation} \label{cose_bpcp12} \]

同理，可以得到\(\delta^3_2\)为：

\[ \begin{equation} \delta^3_2 = (a^3_2 - t_2) \cdot a'(z^3_2) \end{equation} \label{cose_bpcp13} \]

在此基础上，结合我们已知的激活函数为Sigmoid函数\(\sigma(z)\)：

\[ \begin{equation} \begin{split} \begin{cases} \delta^3_1 &= (a^3_1 - t_1) \cdot a'(z^3_1) = (a^3_1 - t_1) \cdot \sigma'(z^3_1) = (a^3_1 - t_1) \cdot \sigma(z^3_1) \cdot \{1 - \sigma(z^3_1)\} \\ \delta^3_2 &= (a^3_2 - t_2) \cdot a'(z^3_2) = (a^3_2 - t_2) \cdot \sigma'(z^3_2) = (a^3_2 - t_2) \cdot \sigma(z^3_2) \cdot \{1 - \sigma(z^3_2)\} \end{cases} \end{split} \end{equation} \label{cose_bpcp14} \]

中间层\(\delta^l_j\)的「反向」递推关系式

之所以引用神经元单元误差的概念，是因为它可以简单地把\(\delta^l_i\)与下一层 \(\delta^l_i\)联系起来。例如，根据偏导数据的链式法则，中间层\(\delta^2_1\)可以 表示为：

\[ \begin{equation} \delta^2_1 = \frac{\partial C}{\partial z^2_1} = \frac{\partial C}{\partial z^3_1} \frac{\partial z^3_1}{\partial a^2_1} \frac{\partial a^2_1}{\partial z^2_1} + \frac{\partial C}{\partial z^3_2} \frac{\partial z^3_2}{\partial a^2_1} \frac{\partial a^2_1}{\partial z^2_1} = ( \frac{\partial C}{\partial z^3_1}\frac{\partial z^3_1}{\partial a^2_1} + \frac{\partial C}{\partial z^3_2}\frac{\partial z^3_2}{\partial a^2_1} ) \frac{\partial a^2_1}{\partial z^2_1} \end{equation} \label{cose_bpmp14} \]

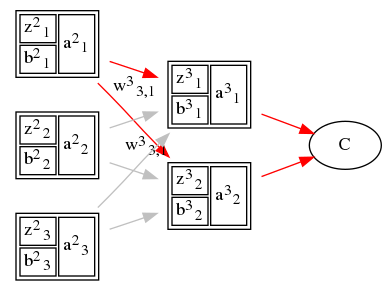
根据\(\delta^3_1\)和\(\delta^3_2\)的定义\ref{cose_bpcp14}可以得到：

\[ \begin{equation} \delta^3_1 = \frac{\partial C}{\partial z^3_1} \quad , \quad \delta^3_2 = \frac{\partial C}{\partial z^3_2} \end{equation} \label{cose_bpmp15} \]

\(z^3_j\)与\(a^2_i\)的关系由公式\ref{vblat_outptlr}求偏导得到：

\[ \begin{equation} \begin{cases} \begin{split} \frac{\partial z^3_1}{\partial a^2_1} = \frac{\partial (w^3_{1,1} \cdot a^2_1 + w^3_{1,2} \cdot a^2_2 + w^3_{1,3} \cdot a^2_3 + b^3_1)}{\partial a^2_1} = w^3_{1,1} \\ \frac{\partial z^3_2}{\partial a^2_1} = \frac{\partial (w^3_{2,1} \cdot a^2_1 + w^3_{2,2} \cdot a^2_2 + w^3_{2,3} \cdot a^2_3 + b^3_2)}{\partial a^2_1} = w^3_{2,1} \end{split} \end{cases} \end{equation} \label{cose_bpmp16} \tag{cose_bpmp16} \]

公式\ref{cose_bpmp14}中\(\frac{\partial a^2_1}{\partial z^2_1}\) 可以直接用激活函数\(a(z)\)的导函数\(a'(z)\)表示：

\[ \begin{equation} \frac{\partial a^2_1}{\partial z^2_1} = a'(z^2_1) \end{equation} \label{cose_bpmp17} \]

把\ref{cose_bpmp15}、\eqref{cose_bpmp16}和\ref{cose_bpmp17}代入公式 \ref{cose_bpmp14}中：

\[ \begin{equation} \delta^2_1 = ( \frac{\partial C}{\partial z^3_1}\frac{\partial z^3_1}{\partial a^2_1} + \frac{\partial C}{\partial z^3_2}\frac{\partial z^3_2}{\partial a^2_1} ) \frac{\partial a^2_1}{\partial z^2_1} = (\delta^3_1 w^3_{1,1} + \delta^3_2 w^3_{2,1}) a'(z^2_1) \end{equation} \label{cose_bpmp18} \]

同样的推导可以推广到\(\delta^2_i\)的通用的关系式：

\[ \begin{equation} \delta^2_i = (\delta^3_1 w^3_{1,i} + \delta^3_2 w^3_{2,i}) a'(z^2_i) \end{equation} \label{cose_bpmp19} \]

同样的推导可以推广到中间层第\(l\)层第\(i\)个神经单元误差\(\delta^l_i\)的通用的关系式 ，\(n\)代表\(l+1\)层神经元的个数：

\[ \begin{equation} \delta^l_i = ( \delta^{l+1}_1 w^{l+1}_{1,i} + \delta^{l+1}_2 w^{l+1}_{2,i} + \cdots + \delta^{l+1}_n w^{l+1}_{n,i} ) a'(z^l_i) \end{equation} \label{cose_bpmp19b} \]

如果要把所有的\(\delta^2_1\)、\(\delta^2_2\)、\(\delta^2_3\)列出来， 用矩阵来描述更加清楚：

\[ \begin{equation} \begin{pmatrix} \delta^2_1 \\ \delta^2_2 \\ \delta^2_3 \\ \end{pmatrix} = \Bigg [ \begin{pmatrix} w^3_{1,1} & w^3_{2,1} \\ w^3_{1,2} & w^3_{2,2} \\ w^3_{1,3} & w^3_{2,3} \\ \end{pmatrix} \begin{pmatrix} \delta^3_1 \\ \delta^3_2 \\ \end{pmatrix} \Bigg ] \odot \begin{pmatrix} a'(z^2_1) \\ a'(z^2_2) \\ a'(z^2_3) \\ \end{pmatrix} \end{equation} \label{cose_bpmp19a} \]

其中\(\delta^3_1\)、\(\delta^3_2\)的矩阵可以用公式\ref{cose_bpsp2}代入。 如果是计算机处理，会把权重那个矩阵以转置矩阵的形式存储， 这样矩阵相乘时的嵌套循环代码看起来更加清楚一点：

\[ \begin{equation} \begin{pmatrix} \delta^2_1 \\ \delta^2_2 \\ \delta^2_3 \\ \end{pmatrix} = \Bigg [ \begin{pmatrix} w^3_{1,1} & w^3_{1,2} & w^3_{1,3} \\ w^3_{2,1} & w^3_{2,2} & w^3_{2,3} \\ \end{pmatrix}^{\mathrm{T}} \begin{pmatrix} \delta^3_1 \\ \delta^3_2 \\ \end{pmatrix} \Bigg ] \odot \begin{pmatrix} a'(z^2_1) \\ a'(z^2_2) \\ a'(z^2_3) \\ \end{pmatrix} \end{equation} \label{cose_bpmp19c} \]

这样就得到了\(\delta^2_i\)与\(\delta^3_j\)的关系，并可以进一步推广为\(l\)层与\(l+1\) 层的一般关系式，其中\(m\)为第\(l+1\)层包含神经元的个数，\(l\)为2以上的整数：

\[ \begin{equation} \delta^l_i = ( \delta^{l+1}_1 w^{l+1}_{1,i} + \delta^{l+1}_2 w^{l+1}_{2,i} + \cdots + \delta^{l+1}_m w^{l+1}_{m,i} ) a'(z^l_i) \end{equation} \label{cose_bpmp20} \]

神经单元误差\(\delta\)避免求导

第二层的神经单元误差\(\delta^2_i\)可以通过公式\ref{cose_bpmp19b}得到， 而公式\ref{cose_bpmp19b}中涉及到的第三层神经单元误差\(\delta^3_1\)和\(\delta^3_2\) 又可以通过公式\ref{cose_bpcp12}与公式\ref{cose_bpcp13}得到。 这样可以避免多次求导操作。例，当激活函数为Sigmoid函数\(\sigma(z)\)时， 用\(\delta^3_1\)和\(\delta^3_2\)来表示\(\delta^2_2 \)：

\[ \begin{equation} \begin{split} \delta^2_2 &= (\delta^3_1 w^3_{1,2} + \delta^3_2 w^3_{2,2}) a'(z^2_2) \\ &= (\delta^3_1 w^3_{1,2} + \delta^3_2 w^3_{2,2}) \sigma'(z^2_2) \\ &= (\delta^3_1 w^3_{1,2} + \delta^3_2 w^3_{2,2}) \sigma(z^2_2) \{1-\sigma(z^2_2)\} \end{split} \end{equation} \label{cose_bpmp21} \]

总结误差反射传播法的步骤

准备学习数据。

初始化权重和偏置的值（通常用随机数，需要反复试错），选一个适当小的正数作为 学习率\(\eta\)（这个「适当」也需要反复试错）。

单个样本

输出层

对于单个样本\(k\)，计算出神经单元的输出值\(a^3_1\)、\(a^3_2\)。 再结合样本\(k\)的正解\(t_1[k]\)、\(t_2[k]\)代入公式\ref{vblat_epta1} 得到单个样本的平方误差\(C_k\)。

\[ z^l_j[k] = \sum^{I}_{i=1} (w^l_{j,i} \cdot a^{l-1}_i[k]) + b^l_j \] \[ a^l_j[k] = a(z^l_j[k]) \] \[ a'^l_j[k] = a'(z^l_j[k]) \] \[ C_k = \frac{1}{2} \sum^{L}_{j=1}(t_j[k] - a^L_j[k])^2 \]

用误差反向传播法计算出各层神经单元误差\(\delta\)。 利用\ref{cose_bpcp11g}求出输出层的神经单元误差，

\[ \frac{\partial C_k}{\partial a^L_j[k]} = a^L_j[k] - t_j[k] \]

根据公式\ref{cose_bpgnl}和神经单元误差\(\delta\)的定义\ref{nnw_nnernd}可以得到 平方误差\(C\)对于权重\(w\)和偏置\(b\)的偏导数：

\[ \frac{\partial C_k}{\partial b^l_j} = \delta^l_j[k] = \frac{\partial C_k}{\partial a^l_j[k]} \cdot a'^l_j[k] \] \[ \frac{\partial C_k}{\partial w^l_{j,i}} = a^{l-1}_{i}[k] \cdot \delta^l_j[k] \]

利用公式\ref{cose_bpmp19b}求出前一层（隐藏层）的神经单元误差 \(\frac{\partial C}{\partial a}\)：

\[ \frac{\partial C_k}{\partial a^{l-1}_i[k]} = \sum^J_{j=1}(w^l_{j,i} \cdot \delta^l_{j,i}[k]) \]

隐藏层

因为当前层的神经单元误差\(\frac{\partial C}{\partial a}\)是由后一层传过来的， 以它为基础求出当前层的平方误差\(C\)对于权重\(w\)和偏置\(b\)的偏导。

还可以算出前一层的神经单元误差\(\frac{\partial C}{\partial a}\)， 继续向前传递（如果有多个隐藏层的话）。

归纳

输出层和隐藏层的操作步骤基本一致。区别在于：

• 隐藏层的\(\frac{\partial C}{\partial a}\)是由后一层传过来的。
• 输出层的\(\frac{\partial C}{\partial a}\)是输出结果和正解的平方错差算出来的

所有样本

得到了每一层所有的\(\frac{\partial C}{\partial b}\)与 \(\frac{\partial C}{\partial w}\)后，根据公式\ref{vblat_eptaexpstpw} 对于所有的样本求和计算出代价函数\(C_{\rm T}\)，还有\(C_{\rm T}\)的梯度\(\nabla C_{\rm T}\)。

\[ C_{\rm T} = \sum^K_{k=1} C_k \] \[ \frac{\partial C_{\rm T}}{\partial b^l_j} = \sum^K_{k=1}\frac{\partial C_k}{\partial b^l_j} \] \[ \frac{\partial C_{\rm T}}{\partial w^l_{j,i}} = \sum^K_{k=1}\frac{\partial C_k}{\partial w^l_{j,i}} \]

下一轮

根据梯度\(\nabla C_{\rm T}\)更新权重和偏置的值(公式\ref{nnw_ffpm})。 如果\(C_{\rm T}\)的误差不符合要求，那么梯度下降以求得更小的精度 下一轮的权重与偏置：

\[ b^l_j = b^l_j + \frac{\partial C_{\rm T}}{\partial b^l_j} \] \[ w^l_{j,i} = w^l_{j,i} \frac{\partial C_{\rm T}}{\partial w^l_{j,i}} \]

重复直到代价函数\(C_{\rm T}\)的值足够小为止。