结构化程序
结构化程序的定义
流程图程序
函数结点
谓词结点

汇点

正规(Proper)程序
- 有一个入口和一个出口。
- 每个结点都能从入口到达,并能从出口离开。
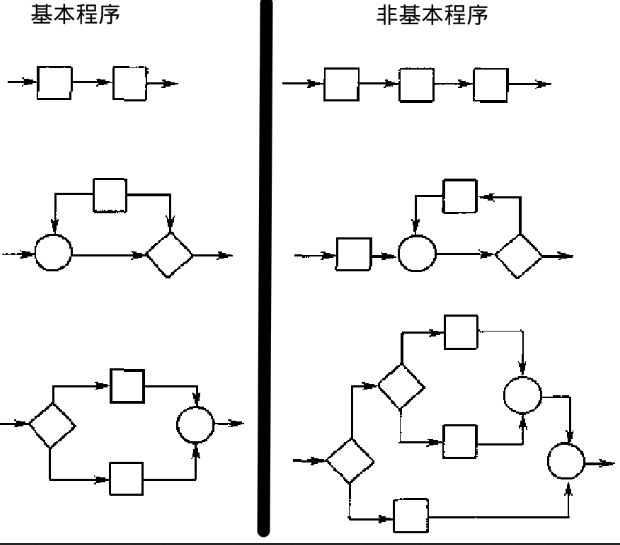
符合正规程序:

非正规程序,因为有无法离开的结点:
非正规程序,因为有无法到达的结点:

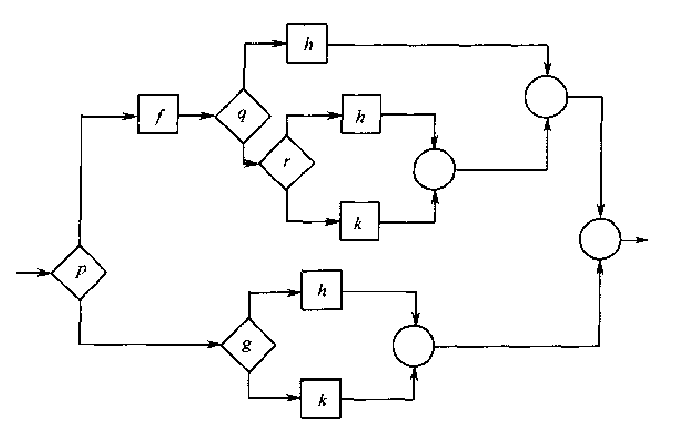
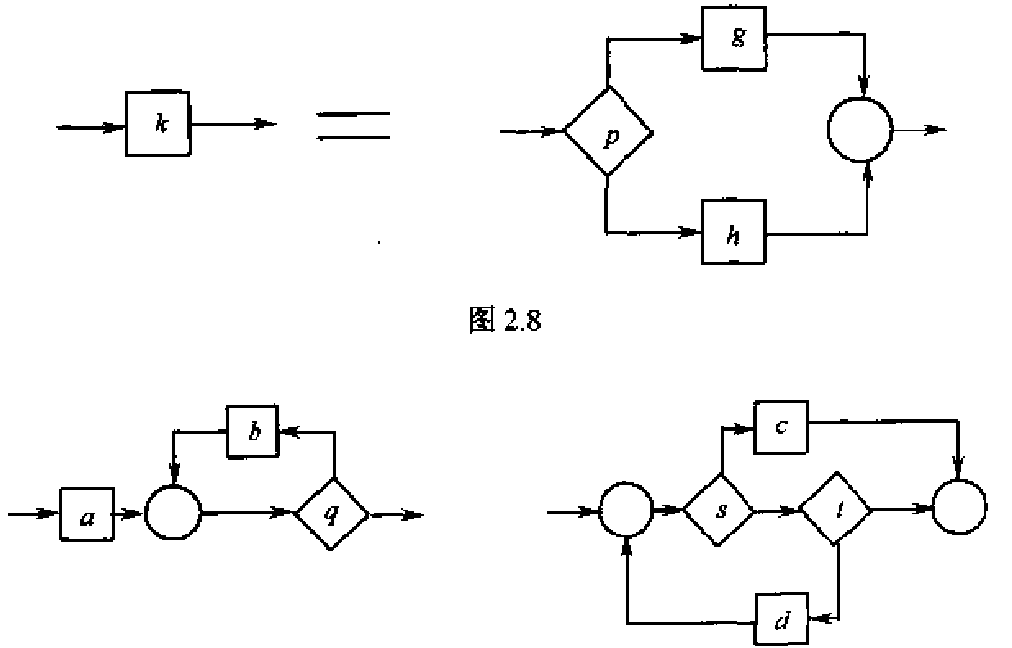
正规程序可以抽象为一个结点。比如以下程序:
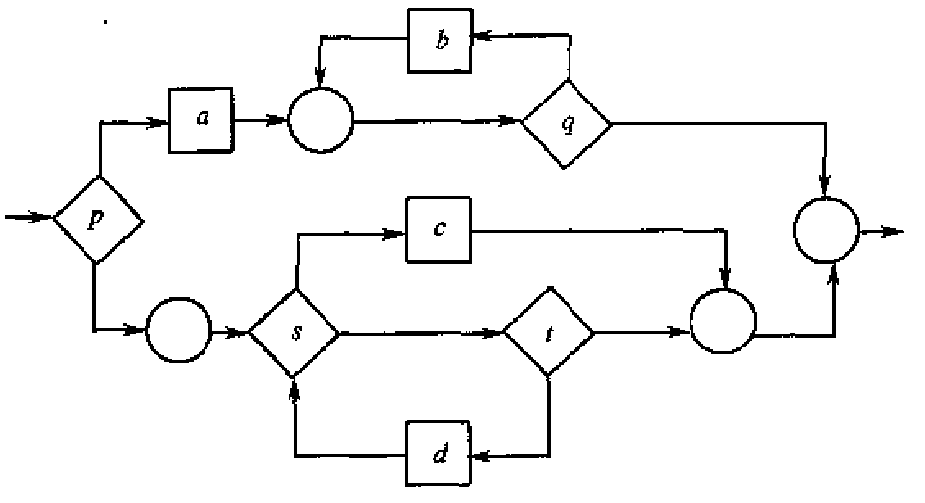
其中的结点可以抽象。最终抽象为只有一个k结点:
基本(Prime)程序
不包含多于一个结点的正规子程序,称为基本程序:
可以总结为7种基本程序:
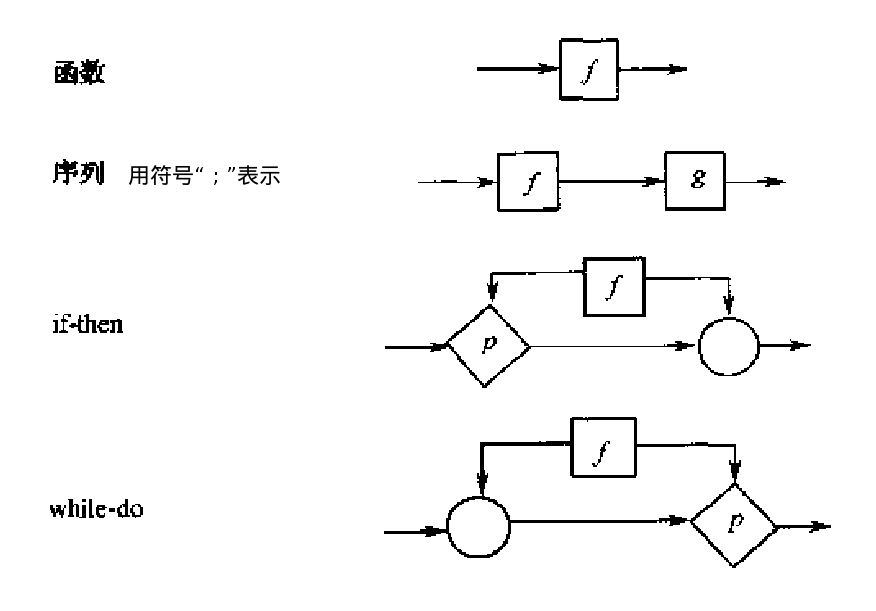
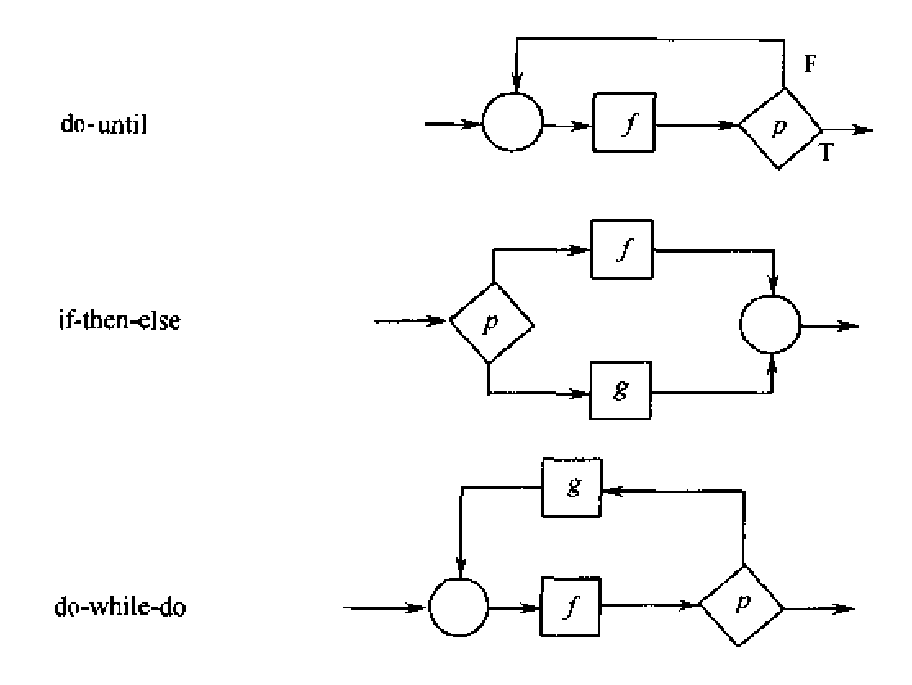
多个基本程序组成一个更大的程序,例如:
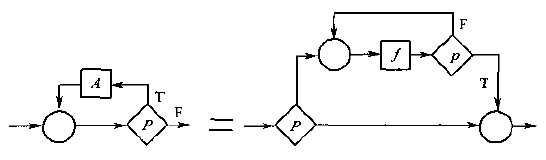
结构化程序
多个基本程序组成复合程序。比如由多个程序\(P1, P2, ..., Pn\)组成的复合程序的全体, 记为:\({P1, P2, ..., Pn}\)。例:
- \(\{;, \text{if-then}\}\)是一个没有循环的程序。
- \(\{;, Repeat\} \subset \{;, \text{if-then}, while\}\)
- \(\{;, \text{if-then-else}, while\} \equiv \{;, \text{if-then-else}, repeat\}\)
- \(\{;, \text{if-then}\}\)与\(\{;, Repeat\}\)无法比较
由基本程序的一个固定的基集合构造出的复合程序称为「结构化程序」。
结构化定理
任何控制结构(即任何正规程序)都可以用三种结构表示出来:
- 序列
- 条件
- 循环
程序函数
- 已知正规程序\(P\),对于每一个初始数据状态\(X\),若程序是终止的,那么有最终数据状态\(Y\)。
- 如果每个\(X\)对应的\(Y\)是唯一的,则对于序对集合\({(X, Y)}\)定义了一个函数, 这个函数被称为\(P\)的「程序函数」,记为\([P]\)。
以程序P为例:
t := x x := y y := t
对于给定的集合\(X: (x, y, t)\)结果为\(Y: (y, x, x)\)。所以程序函数为:
\[ \begin{equation} \{(x, y, t),(y, x, x)\} \end{equation} \]又例如:
if x < y then z := x else z := y fi
是一个基本程序,它的程序函数是:
\[ \begin{equation} \{ ((x, y, z), (x, y, min(x, y)) \} \end{equation} \]用条件规则式表达为:
\[ \begin{equation} \{ (x, y, z) \; | \; x \lt y \to z:=x \land x \gt y \to z := y\} \end{equation} \]也可以简写为数据赋值形式:
\[ \begin{equation} (z:=min(x,y)) \end{equation} \]7种基本程序的程序函数表示:
\[ \begin{equation} \begin{split} [f] = & \{(x,y) \; | \; y=f(x)\} \\ [f;g] = & \{(x,y) \; | \; y=g \cdot f(x)\} \\ [\text{if-then}] = & \{(x,y) \; | \; p(x) \to y=f(x) \; | \; \neg p(x) \to y=x \} \\ [\text{while-do}] = & \{(x,y) \; | \owns k \gt 0 \; ((\forall j, 1 \lt j \lt k) \\ & (p \cdot f^i(x)) \land \neg p \cdot f^k(x) \to y = f^k(x)) \} \\ [\text{do-while}] = & \{(x,y) \; | \owns k \gt 0 \; ((\forall j, 1 \lt j \lt k) \\ & (\neg p \cdot f^i(x)) \land p \cdot f^k(x) \to y = f^k(x)) \} \\ [\text{if-then-else}] = & \{(x,y) \; | \; p(x) \to y=f(x) \; | \; \neg p(x) \to y= g(x) \} \\ [\text{do-while-do}] = & \{(x,y) \; | \owns k \gt 0 \; ((\forall j, 0 \lt j \lt k) p \cdot f(g \cdot f)^i(x)) \land \\ & \neg p \; f(g \cdot f)^k(x) \to y = f \cdot (g \cdot f)^k(x) \} \end{split} \end{equation} \]- \(g \cdot f(x)\)表示函数复合,即:\(g(f(x))\);
- \(f^k(x)\)表示同一函数的重复复合,即:\(f^0(x)=x, f^k(x)=f \cdot f^{k-1}(x)\), 其中\(k=1,2,\cdots\)
定义:如果程序\(P_1\)和\(P_2\)有相同的程序函数,则称它们是函数等价的,或简称是等价的。
结构化定理
结构化定理:任何一个正规程序都可以函数等价于一个由基集合\(\{;, \text{if-then-else},\text{while-do}\}\) 产生的程序。
证明过程:
首先,从程序的入口开始给程序的函数结点和谓词结点编号(1, 2, ..., n), 函数结点和谓词的出口那条线也要编号,线条的编号为下一个结点的编号。 如果线后面没有结点,那么线的编号就是\(0\)。
然后,把每一个函数结点\(h\),需要根据它的编号为\(i\)和它的出口线编号为\(j\), 全部构造为序列程序\(g_i\):
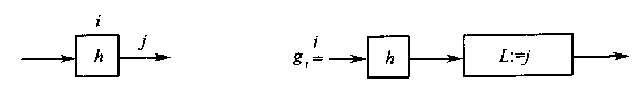
对于每个谓词结点\(p\),需要根据它的编号\(i\)和两条出口线\(j\)、\(k\), 构造一个新的\(\text{if-then-else}\)程序\(g_i\):
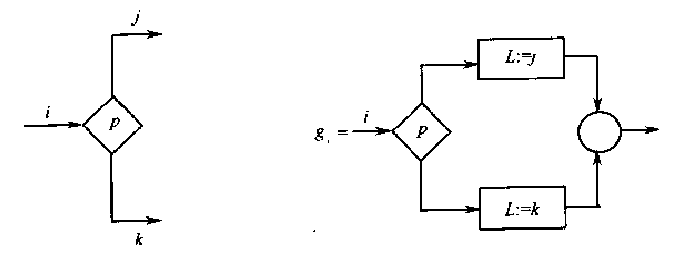
最后根据全部的\(g_i\)(其中\(i = 1,2,\cdots,n\))构造一个\(\text{while-do}\)循环, 循环体是\(L\)值从\(1\)到\(n\)进行测试嵌套的\(\text{if-then-else}\)程序, 最内层的\(I\)表示恒等函数:
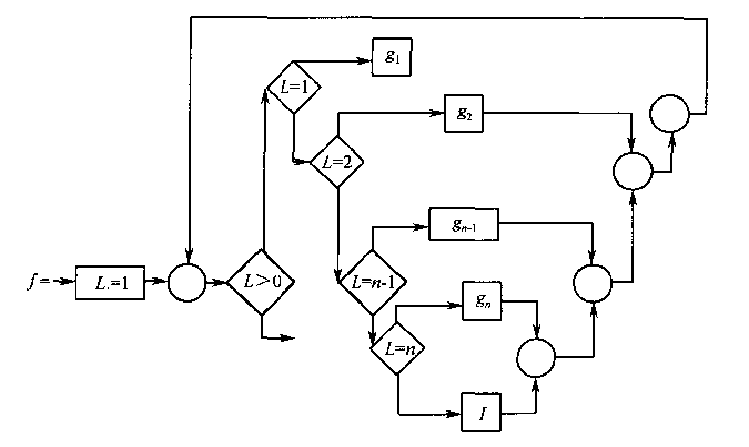
例子,下图中已经加上编号了:
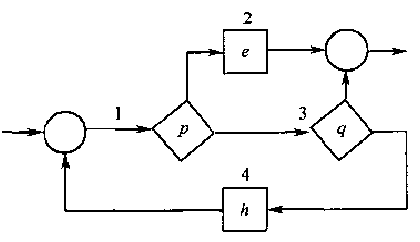
每个结点转为序列:
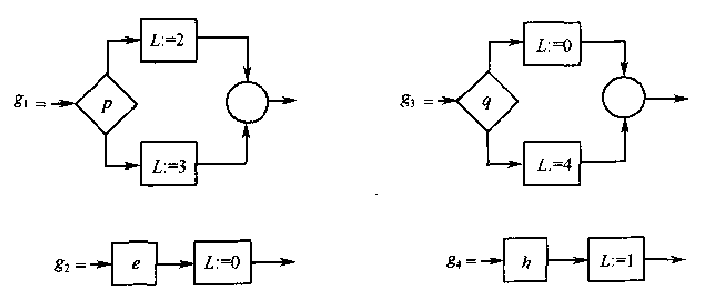
虽然\(\{;, \text{if-then-else},\text{while-do}\}\)可以表示任何复杂的控制结构, 但这并不是唯一的方法。例如\(\{;, \text{if-then-else},\text{do-until}\}\) 也可以表示所有的正规程序:
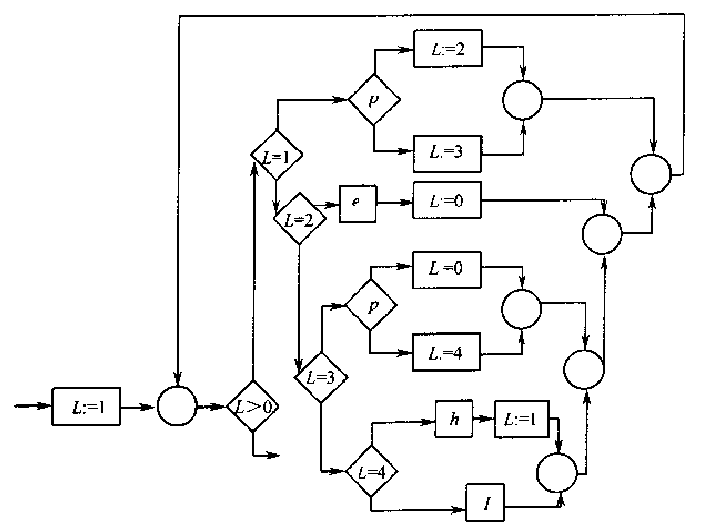
递归结构程序
上面的例子可以看出结构化程序比较庞大而且效率不高。有一些对于\(L\)的测试和赋值是多余的, 可以消除掉。
对于某些\(j \gt 0\),如果\(g_j\)中不包含赋值\(L := j\),可以用\(g_j\)代替所有的赋值操作\(L := j\)。 这样\(j\)不再赋值给\(L\),所以就不用在\(\text{if-then-else}\)中就不用测试\(I = j\)。 这个替换过各可以一直继续到发现以下两种情况为止:
- 除了\(L := 0\)以外所有对\(L\)的赋值操作都被消除。
- 每个余下的\(g'_i\)中都包含相应的赋值操作\(L := i\)。 其中\(g'_i\)是\(gi\)经过一些替换后得到的复合程序。
注意对包含\(L := i\)的\(g'_i\)不能替换,因为这样替换以后并不能消除赋值\(L := i\)。
采用以上步骤的程序通常称为递归结构程序。
例子,对于以下程序的简化步骤:

用\(g_4\)代替赋值操作\(L := 4\),并消除\(L := 4\)得到:
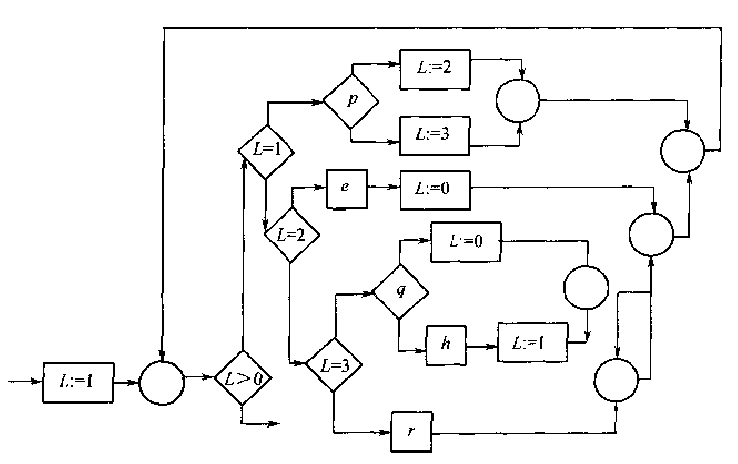
用代换后得到的\(g'_3\)(即\(L=3\)通路上的\(\text{if-then-else}\)程序)代替赋值操作\(L := 3\), 并消除测试\(L = 3\),得到:
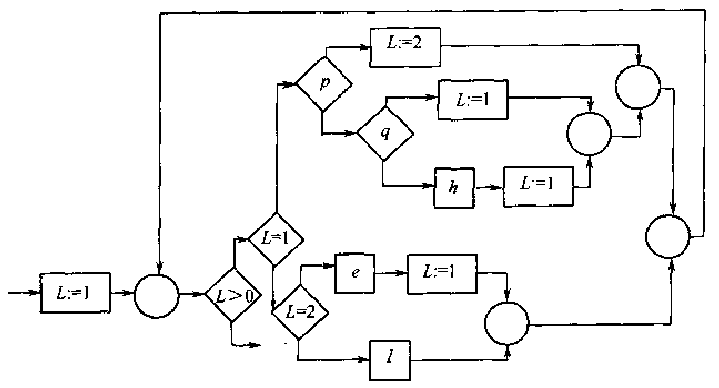
用\(g_2\)代替赋值操作\(L := 2\),得到:
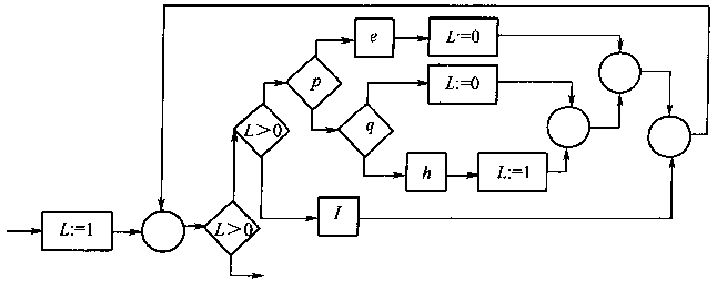
这时代换以后得到\(g'_1\)中包含赋值操作\(L := 1\),因而不能再进一步替换。 但是在这个程序中\(L\)的初始值为\(1\),而且仅在程序出口处才变为\(0\), 所以在循环中赋值操作\(L := 1\)和测试操作\(L := 1\)是不需要的,消除以后得到:
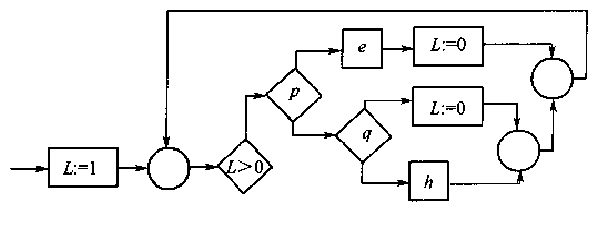
另一个例子,以下程序是个无限循环例子:
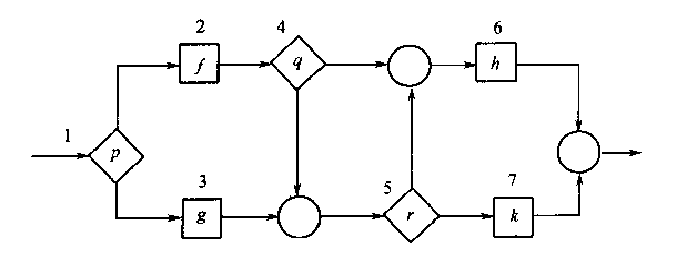
转为结构化程序为(其中为了看起来清楚,把嵌套的\(\text{if-then-else}\)改为CASE结构):
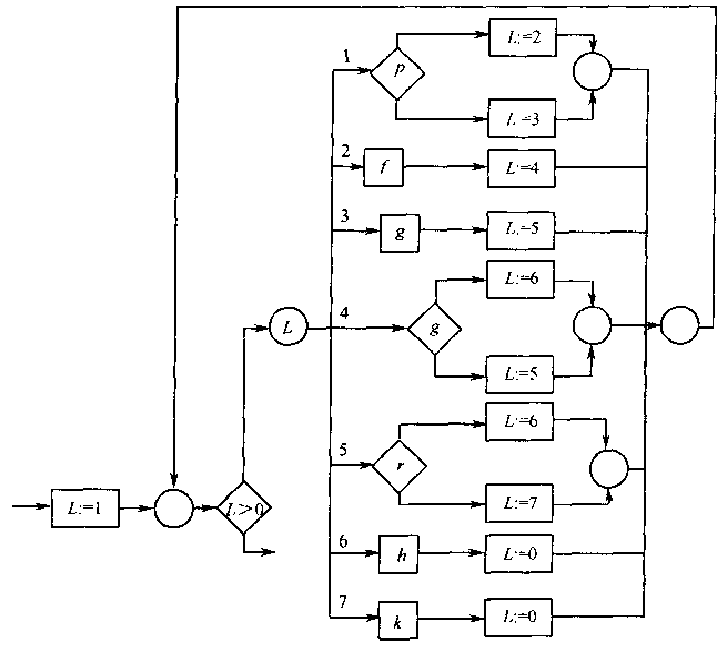
继续按本节介绍的方法替换,会得到这样的递归程序:
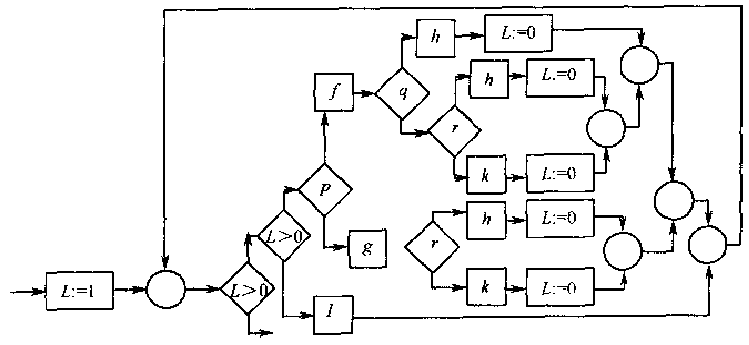
这样每条通路上都有\(L := 0\),所以无论哪条通路都会让循环体执行一次以后直接退出循环。 所以,赋值操作\(L := 0\)和测试\(L > 0\)和循环都可以消除,接下来\(L := 1\)也可以消除。 最后得到以下简单复合程序: