Jade Dungeon

Scala相关数学概念

代数数据类型

代数数据类型（algebraic data type）通过数学上代数的特性来讨论编程时用到的数据结构。

Scala中把数据类型分为「乘法类型」（product type）和「加法类型」（sum type）。

乘法类型

乘法类型非常常用，以case类型的Person作为例子，包含名字和年龄两个属性：

case class Persion(name: Name, age: Age)

对于这个类型，代表姓名的Name类型有无限种可能性，代表年龄的Age类型取值范围为\((0, 130]\)之内的整数。所以Person类可能的取值范围为\(N \times 131\)。

`Product`类型

在Scala中Product类型抽象了乘法类型，并且它是所有TupleN和Case类的父类。

`Unit`类型

Unit类型只有一个实例()，代表没有任何元素的空元组。没有元素的元组只能有一个实例，因为它不能具有任何状态。

(Int, String, Unit)可能存在的实例个数与(Int, String)相同。即： \((M \times N \times 1) = (M \times N)\)

Unit（单位）这个名字代表了它是乘法中最小的单位，即\(1\)。

`Nothing`类型

scala.Nothing类型抽象了乘法类型中零个实例的情况。它与任何其他类型结合，产生出了新类型也只有零个实例。没有任何实例可以「装下」Nothing类型。

加法类型

加法类型的每个值都是互拆的。

Scala中加法类型的代表是枚举类型和封闭继承类型。

枚举类：适合于仅仅带索引的标志位。
封闭类型：适用于需要携带比较多的可选值。

枚举类型

枚举是典型的加法类型，每个值都是互斥的：

object WeekDay extends Enumeration {
	type WeekDay = Value
		val Sunday    = Value("Sunday")
		val Monday    = Value("Monday")
		val Tuesday   = Value("Tuesday")
		val Wednesday = Value("Wednesday")
		val Thursday  = Value("Thursday")
		val Firday    = Value("Firday")
		val Saturday  = Value("Saturday")
}

封闭继承类型（sealed hierarchy of object）

sealed trait WeekDay { val name: String }

case object Sunday    extends WeekDay { val name = "Sunday"    }
case object Monday    extends WeekDay { val name = "Monday"    }
case object Tuesday   extends WeekDay { val name = "Tuesday"   }
case object Wednesday extends WeekDay { val name = "Wednesday" }
case object Thursday  extends WeekDay { val name = "Thursday"  }
case object Firday    extends WeekDay { val name = "Firday"    }
case object Saturday  extends WeekDay { val name = "Saturday"  }

代数数据类型的属性

乘法类型的交换率：

Nothing * (Int, String, Boolean) == (Int, String, Boolean) * Nothing 
Unit    * (Int, String, Boolean) == (Int, String, Boolean) * Unit    
WeekDay * (Int, String, Boolean) == (Int, String, Boolean) * WeekDay

Nothing + (Sunday, Monday, Tuesday) == (Sunday, Monday, Tuesday) + Nothing 
Unit    + (Sunday, Monday, Tuesday) == (Sunday, Monday, Tuesday) + Unit    
Person  + (Sunday, Monday, Tuesday) == (Sunday, Monday, Tuesday) + Person

更多细节

代数的意义

引入代数的概念，是为了让开发者审视自己的类型设计在逻辑上是否能自圆其说。防范一些在逻辑上的Bug。例如：

Scala中的List是一个抽象类，它的两个子类Nil和::抽象了空列表和非空列表。这种抽象看起来像是废话，但是在实际应用中，这两种类型可以构造出不同的实例，可以非常精确地定义对于同一种操作，在列表为空和非空时应该表现出来的行为。

群论（Goup）

群表示一个拥有满足封闭性、结合律、有单位元、有逆元的二元运算的代数结构。若群\(G\)中元素个数是有限的，则\(G\)称为有限群。否则称为无限群。

http://www.wlxt.uestc.edu.cn/wlxt/ncourse/lsxx/web/lssx/end/imgs/16/ls16.2/16.2.1.htm

二元代数系统

\(G\)代表集合，\(\circ\)代表可以应用到\(G\)中元素类型的操作，那么可以用\(<G, \circ >\)来表示一个二元代数系统。例如：

<整数, 加法>
<整数, 乘法>
<字段串, 拼接>

二元代数系统满足封闭性（Closure），对于任意\(\forall a,b \in G\)，有\(a \circ b \in G\)。

对应到Scala中就是：对字符串类型（集合）与拼接操作（操作），返回值也是字符串。这样的组合满足封闭性，所以字符串与拼接操作可以形成的二元代数系统，

半群（SemiGroup）

群必须是二元代数系统，所以群必须满足封闭性。如果在满足封闭性的前提下还满足结合律，那么这个二元代数系统就是一个半群：

结合律（Associativity）：在\(G\)中是可结合的，即\(\forall a,b,c \in G\)，都有\((a \circ b) \circ c = a \circ (b \circ c)\)；

(("foo" + "bar") + "helloword") == ("foo" + ("bar" + "helloword"))
                                          //> res0: Boolean = true

((3 + 2) + 1) == (3 + (2 + 1))            //> res1: Boolean = true
((3 * 2) * 1) == (3 * (2 * 1))            //> res2: Boolean = true

((true || false) || true) == (true || (false || true))
                                          //> res3: Boolean = true

((true && false) && true) == (true && (false && true))
                                          //> res3: Boolean = true

用类来抽象：半群是一组对象的集合，满应足封闭性和结合性。A表示群的构成对象， op表示两个对象的结合，它的封闭性由返回值的抽象类型A保证。

(("foo" + "bar") + "helloword") == ("foo" + ("bar" + "helloword"))
                                                       //> res0: Boolean = true
((3 + 2) + 1) == (3 + (2 + 1))                         //> res1: Boolean = true
((3 * 2) * 1) == (3 * (2 * 1))                         //> res2: Boolean = true
((true || false) || true) == (true || (false || true)) //> res3: Boolean = true
((true && false) && true) == (true && (false && true)) //> res4: Boolean = true

/* 半群的抽像 */
trait SemiGroup[A] {

  def op(a1: A, a2: A): A
  
}

幺半群（Monoid）

单位元或幺元（Identity）：\(G\)中存在关于\(\circ\)的幺元\(e\)，即\(\exists e \in G\)，使得\(\forall a \in G\)，都有\(e \circ a = a \circ e = a\)；

用Scala来举例子，对于字符串和拼接操作组成的半群，有一个特殊的字符串""。任何一个字符串和""进行拼接操作，返回的结果都是这个字符串本身。例：

(a: String)  => a == (a + ""    ) == (""    +  a) // 字符串与拼接的幺元是 `""`
(n: Int)     => n == (n +  0    ) == (0     +  n) // 整数与加法的幺元是 `0`
(n: Int)     => n == (n *  1    ) == (1     *  n) // 整数与乘法的幺元是 "1"
(b: Boolean) => b == (b || false) == (false || b) // 布尔与或的幺元是 `false`
(b: Boolean) => b == (b && true ) == (true  || b) // 布尔与与的幺元是 "true"

可以看到对于不同集合与操作组成的幺半群群，它们的操作行为和幺元是不一样的。当自己实现一个群时一定要注意这点。整数加法的的幺半群实现，它的幺元是0，整数乘法的的幺半群实现，它的幺元是1。

逆元：\(G\)中每个元素\(a\)都有逆元\(a^{-1}\)，即\(\forall a \in G\)，都\(\exists a^{-1} \in G\)，使得\(a \circ a^{-1} = a^{-1 \circ a} = e\)。

这个程序里暂时用不到，不解释了。

如果一个半群有幺元并且每个元有逆元，那么这个群肯定是含幺半群。

(a: String)  => { a == (a + "")     == ("" + a)     } // always return true
(n: Int)     => { n == (n + 0)      == (0 + n)      } // always return true
(n: Int)     => { n == (n * 1)      == (1 * n)      } // always return true
(b: Boolean) => { b == (b || false) == (false || b) } // always return true
(b: Boolean) => { b == (b && true)  == (true || b)  } // always return true

幺元应用到flod操作：

((("" + "hello ") + "world ") + "monoid")       
                                 //> res10: String = hello world monoid
List("hello ", "world ", "monoid").foldLeft("")((a, b) => { a + b })
                                 //> res11: String = hello world monoid

(((0 + 1) + 2) + 3)                             //> res12: Int = 6
List(1, 2, 3).foldLeft(0)(_ + _)                //> res13: Int = 6

(((1 * 1) * 2) * 3)                             //> res14: Int = 6
List(1, 2, 3).foldLeft(1)(_ * _)                //> res15: Int = 6

(((false || true) || false) || true)            //> res16: Boolean = true
List(true, false, true).foldLeft(false)(_ || _) //> res17: Boolean = true

(((true && true) && false) && true)             //> res18: Boolean = false
List(true, false, true).foldLeft(true)(_ || _)  //> res19: Boolean = true

还可以通过结合律并行执行：

List(0, 1, 2, 3, 4, 5, 6, 7, 8, 9).foldLeft(0)(_ + _)
                                                //> res20: Int = 45

((((((((((0 + 0) + 1) + 2) + 3) + 4) + 5) + 6) + 7) + 8) + 9)
                                                //> res21: Int = 45

(0 + (0 + (1 + (2 + (3 + (4 + (5 + (6 + (7 + (8 + 9))))))))))
                                                //> res22: Int = 45

(0 + //
  (((((0 + 0) + 1) + 2) + 3) + 4) + //
  (((((0 + 5) + 6) + 7) + 8) + 9))              //> res23: Int = 45

幺半群是半群的子集，并且存在一个幺元：

用Scala来实现幺半群是半群的子集，并且存在一个幺元：

/* 幺半群的抽像  */
trait Monoid[A] extends SemiGroup[A] {

  def zero: A
  
}

val stringMonoid = new Monoid[String] {

  def op(a1: String, a2: String) = a1 + a2

  def zero = ""
}

val intAdditionMonoid = new Monoid[Int] {
  def op(a1: Int, a2: Int) = a1 + a2
  def zero = 0
}

val intMultiplyMonoid = new Monoid[Int] {
  def op(a1: Int, a2: Int) = a1 * a2
  def zero = 1
}

`String`类型与拼接操作的幺半群实现，它的幺元是空字符串：

{{{class="brush: scala"
val stringMonoid = new Monoid[String] {
  def op(a1: String, a2: String) = a1 + a2
  def zero = ""
}

val booleanOrMonoid = new Monoid[Boolean] {

	def op(a1: Boolean, a2: Boolean) = a1 || a2

	def zero = false

}

val booleanAndMonoid = new Monoid[Boolean] {

	def op(a1: Boolean, a2: Boolean) = a1 && a2

	def zero = true

}

更加抽象一步，如果我们把集合也作为一个集合：

列表类型与拼接操作的幺半群实现，它的幺元是空列表：

/* 列表类型与拼接操作的幺半群实现，它的幺元是空列表： */
def listMonoid[A] = new Monoid[List[A]] {
  def op(a1: List[A], a2: List[A]) = a1 ++ a2
  def zero = Nil
}

Option类型与取值操作的幺半群实现，它的幺元是空：

def optionMonoid[A] = new Monoid[Option[A]] {
  def op(a1: Option[A], a2: Option[A]) = a1 orElse a2
  def zero = None
}

自函子类型与组合操作的幺半群实现。

函数是值到值的映射，函子就是类型到类型的映射。
自函数（endofunctor）是参数值和返回值相同函数。
自函子（identity）就是参数类型与返回类型相同的函子。

def endoMonoid[A]: Monoid[A => A] = new Monoid[A => A] {
  def op(f: A => A, g: A => A) = f compose g // f(g())
  val zero = (a: A) => a                     // identity
}

检查Monoid

/* 检查Monoid的结合性 */
def checkAssociativity[A](m: Monoid[A], a: A, b: A, c: A): Boolean =
  m.op(a, m.op(b, c)) == m.op(m.op(a, b), c)

/* 检查Monoid的幺元 */
def checkIdentity[A](m: Monoid[A], a: A): Boolean =
  m.op(a, m.zero) == a && m.op(m.zero, a) == a

使用monoid折叠列表

把实现的Monoid类代入到flod操作中，「幺元」与「操作」正好对应了flod方法的两个参数：

val words = "Hic" :: "Est" :: "Index" :: Nil    
//> words  : List[String] = List(Hic, Est, Index)

val s = words.foldLeft(stringMonoid.zero)(stringMonoid.op)
//> s  : String = HicEstIndex

val t = words.foldRight(stringMonoid.zero)(stringMonoid.op)
//> t  : String = HicEstIndex

((("" + "Hic") + "Est") + "Index") == ("" + ("Hic" + ("Est" + "Index")))
//> res24: Boolean = false

实现一个通用的concatenate函数用来折叠列表：

对于类型A，如果有现成的Monoid[A]，那么可以保证折叠操作的正确。因为Monoid从数学上保证了的列表的元素类型、操作类型与幺元三者的匹配。

def concatenate[A](as: List[A], m: Monoid[A]): A = {
	as.foldLeft(m.zero)(m.op)
}

如果类型A不是Monoid类型怎么办？想办法把它转为Monoid类型B：

def foldMap[A, B](as: List[A], m: Monoid[B])(f: A => B): B =
	as.foldLeft(m.zero)((b, a) => m.op(b, f(a)))

上面的例子使用flodLeft方法来实现flodMap，反过来也可能用flodMap来实现 flodLeft

def dual[A](m: Monoid[A]): Monoid[A] = new Monoid[A] {
  def op(x: A, y: A): A = m.op(y, x)
  val zero = m.zero
}

def foldLeft[A, B](as: List[A])(z: B)(f: (B, A) => B): B =
  foldMap(as, dual(endoMonoid[B]))(a => b => f(b, a))(z)

def foldRight[A, B](as: List[A])(z: B)(f: (A, B) => B): B =
  foldMap(as, endoMonoid[B])(f.curried)(z)

分段并行地折叠操作

把集合拆成两部分，然后递归地处理每一部分：

indexedSeq作为不可变的集合，支持高效地随机访问，也提供了现成的splitAt和 length方法：

def foldMapV[A, B](as: IndexedSeq[A], m: Monoid[B])(f: A => B): B = {
  if (as.length == 0) {
    m.zero
  } else if (as.length == 1) {
    f(as(0))
  } else {
    val (l, r) = as.splitAt(as.length / 2)
    m.op(foldMapV(l, m)(f), foldMapV(r, m)(f))
  }
}

使用flodMap来判断序列是否是有序的：

def ordered(ints: IndexedSeq[Int]): Boolean = {
	// Our monoid tracks the minimum and maximum element seen so far
	// as well as whether the elements are so far ordered.
	val mon = new Monoid[Option[(Int, Int, Boolean)]] {
		def op(
				o1: Option[(Int, Int, Boolean)], 
				o2: Option[(Int, Int, Boolean)]
		) = (o1, o2) match {
			// The ranges should not overlap if the sequence is ordered.
			case (Some((x1, y1, p)), Some((x2, y2, q))) => 
				Some((x1 min x2, y1 max y2, p && q && y1 <= x2))
			case (x, None) => x
			case (None, x) => x
		}
		val zero = None
	}
	// The empty sequence is ordered, 
	// and each element by itself is ordered.
	foldMapV(ints, mon)(i => Some((i, i, true))).map(_._3).getOrElse(true)
}

把长文本递归地分成两段，并计算单词数量（根据空格出现的次数）：

sealed trait WC
case class Stub(chars: String) extends WC
case class Part(lStub: String, rStub: String, number: Int) extends WC

val wcMonoid: Monoid[WC] = new Monoid[WC] {
	// The empty result, where we haven't seen any characters yet.
	val zero = Stub("")

	def op(a: WC, b: WC) = (a, b) match {
		case (Stub(c), Stub(d))       => Stub(c + d)
		case (Stub(c), Part(l, r, n)) => Part(c + l, r, n)
		case (Part(l, r, n), Stub(c)) => Part(l, r + c, n)
		case (Part(l1, r1, n1), Part(l2, r2, n2)) =>
			Part(l1, r2, n1 + (if ((r1 + l2).isEmpty) 0 else 1) + n2)
	}
}

def count(s: String): Int = {
	// A single character's count. Whitespace does not count,
	// and non-whitespace starts a new Stub.
	def wc(c: Char): WC = if (c.isWhitespace) {
		Part("", "", 0)
	} else { Stub(c.toString) }

	// `unstub(s)` is 0 if `s` is empty, otherwise 1.
	def unstub(s: String) = s.length min 1

	foldMapV(s.toIndexedSeq, wcMonoid)(wc) match {
		case Stub(s)			 => unstub(s)
		case Part(l, r, n) => unstub(l) + unstub(r) + n
	}
}

Monoid同态

分别取长度再相加，与连接字符串取长度结果是一样的：

"foo".length + "bar".length == ("foo" + "bar").length
//> res30: Boolean = true

length:     String => Int
   add: (Int, Int) => Int

length函数把String转为Int并保存monoid结构，这样的函数称为monoid同态（honomorphism）。

一个monoid同态f定义为在monoid M和N之间对所有的值及x和y都遵守以下法则：

M.op(f(x), f(y)) == f(N.op(x, y))

对应到上面的例子就是：

val strAddMonoid = new Monoid[String] {
	def op(a1: String, a2: String) = a1 + a2
	def zero = ""
}

val intAddMonoid = new Monoid[Int] {
	def op(a1: Int, a2: Int) = a1 + a2
	def zero = 0
}

intAddMonoid.op(strLen(x), strLen(y)) == strLen(strAddMonoid.op(x, y))

同态在设计类库时有十分有用，如果两个类型是monoid并且它们之间存在函数，好的做法是考虑这个函数是否可以保持monoid结构，并测试其是否为monoid同态。

Monoid同质

某些情况下两个monoid之间是双向同态的，称为同质（isomorphic，前缀iso表示相等）。在两个monoid M和N之间存在两个同态函数f和g，而且f andThen g和g andThen f是同等的函数。

例如，String和List[Char] monoid的连接操作是同质的：

def listAddMonoid[A] = new Monoid[List[A]] {
	def op(a1: List[A], a2: List[A]) = a1 ++ a2
	def zero = Nil
}

val charListMonoid = listAddMonoid[Char]
// ch10.monoid.group.Monoid[List[Char]]{
//   def zero: scala.collection.immutable.Nil.type
// } = ch10.monoid.group.MonoidExample$$anon$6@47f6473


val stringAddMonoid = new Monoid[String] {
	def op(a1: String, a2: String) = a1 + a2
	def zero = ""
}

monoid(false, ||)和monoid(true, &&)通过取反操作!是同质的：

val booleanOrMonoid = new Monoid[Boolean] {
	def op(a1: Boolean, a2: Boolean) = a1 || a2
	def zero = false
}

val booleanAndMonoid = new Monoid[Boolean] {
	def op(a1: Boolean, a2: Boolean) = a1 && a2
	def zero = true
}

booleanOrMonoid.op(!(false), !(true)) == 
	!(booleanAndMonoid.op(false, true)) //> res33: Boolean = true
	
booleanAndMonoid.op(!(true), !(false)) == 
	!(booleanOrMonoid.op(true, false)) //> res34: Boolean = true

可折叠的数据结构

无论容器的结构是列表、树、流等等，只要确定是可折叠的，就可以通过flodRight 来汇总。

例如确定可折叠容器中元素是整数，就可以通过flodRight求和：

ints.foldRight(0)(_ + _)

把可折叠性抽象为Foldable特质：

trait Foldable[F[_]] {
	import Monoid._

	def foldRight[A,B](as: F[A])(z: B)(f: (A, B) => B): B =
	  foldMap(as)(f.curried)(endoMonoid[B])(z)

	def foldLeft[A,B](as: F[A])(z: B)(f: (B, A) => B): B =
	  foldMap(as)(a => (b: B) => f(b, a))(dual(endoMonoid[B]))(z)

	def foldMap[A, B](as: F[A])(f: A => B)(mb: Monoid[B]): B =
	  foldRight(as)(mb.zero)((a, b) => mb.op(f(a), b))

	def concatenate[A](as: F[A])(m: Monoid[A]): A =
	  foldLeft(as)(m.zero)(m.op)

	def toList[A](as: F[A]): List[A] =
	  foldRight(as)(List[A]())(_ :: _)
}

可折叠的列表实现：

object ListFoldable extends Foldable[List] {

	override def foldRight[A, B](as: List[A])(z: B)(f: (A, B) => B) =
	  as.foldRight(z)(f)

	override def foldLeft[A, B](as: List[A])(z: B)(f: (B, A) => B) =
	  as.foldLeft(z)(f)

	override def foldMap[A, B](as: List[A])(f: A => B)(mb: Monoid[B]): B =
	  foldLeft(as)(mb.zero)((b, a) => mb.op(b, f(a)))

	override def toList[A](as: List[A]): List[A] = as

}

可折叠的序列：

object IndexedSeqFoldable extends Foldable[IndexedSeq] {
	import Monoid._

	override def foldRight[A, B](as: IndexedSeq[A])(z: B)(f: (A, B) => B) =
	  as.foldRight(z)(f)

	override def foldLeft[A, B](as: IndexedSeq[A])(z: B)(f: (B, A) => B) =
	  as.foldLeft(z)(f)

	override def foldMap[A, B](as: IndexedSeq[A])(f: A => B)(mb: Monoid[B]): B =
	  foldMapV(as, mb)(f)

}

可折叠的流：

object StreamFoldable extends Foldable[Stream] {

	override def foldRight[A, B](as: Stream[A])(z: B)(f: (A, B) => B) =
	  as.foldRight(z)(f)

	override def foldLeft[A, B](as: Stream[A])(z: B)(f: (B, A) => B) =
	  as.foldLeft(z)(f)

}

可折叠的二叉树实现。注意在flodMap树的时候不会用到幺元，因为不在空的二叉树。所以这里二叉树只是一个半群，而不是幺半群。

sealed trait Tree[+A]
case class Leaf[A](value: A) extends Tree[A]
case class Branch[A](left: Tree[A], right: Tree[A]) extends Tree[A]

object TreeFoldable extends Foldable[Tree] {

	override def foldMap[A, B](as: Tree[A])(f: A => B)(mb: Monoid[B]): B = as match {
	  case Leaf(a) => f(a)
	  case Branch(l, r) => mb.op(foldMap(l)(f)(mb), foldMap(r)(f)(mb))
	}

	override def foldLeft[A, B](as: Tree[A])(z: B)(f: (B, A) => B) = as match {
	  case Leaf(a) => f(z, a)
	  case Branch(l, r) => foldLeft(r)(foldLeft(l)(z)(f))(f)
	}

	override def foldRight[A, B](as: Tree[A])(z: B)(f: (A, B) => B) = as match {
	  case Leaf(a) => f(a, z)
	  case Branch(l, r) => foldRight(l)(foldRight(r)(z)(f))(f)
	}
	
}

可折叠的Option实现：

object OptionFoldable extends Foldable[Option] {

	override def foldMap[A, B](as: Option[A])(f: A => B)(mb: Monoid[B]): B =
	  as match {
	    case None => mb.zero
	    case Some(a) => f(a)
	  }

	override def foldLeft[A, B](as: Option[A])(z: B)(f: (B, A) => B) = as match {
	  case None => z
	  case Some(a) => f(z, a)
	}

	override def foldRight[A, B](as: Option[A])(z: B)(f: (A, B) => B) = as match {
	  case None => z
	  case Some(a) => f(a, z)
	}

}

组合monoid为product

如果类型A与B是monoid，那么tuple类型(A, B)也是monoid，称为product。

当A.op与B.op是可结合的（associative），那么如下的op实现也是可结合的：

def productMonoid[A,B](A: Monoid[A], B: Monoid[B]): Monoid[(A, B)] = {

	new Monoid[(A, B)] {

		def op(x: (A, B), y: (A, B)) = (A.op(x._1, y._1), B.op(x._2, y._2))

		val zero = (A.zero, B.zero)

	}

}

把容器组装为monoid

如果元素是monoid，某些容器就可以构建成monoid。比如Map中的value是monoid，把合并key-value的操作构建成monoid：

def mapMergeMonoid[K, V](vMonoid: Monoid[V]): Monoid[Map[K, V]] =
	new Monoid[Map[K, V]] {
		def op(a: Map[K, V], b: Map[K, V]) = {
			(a.keySet ++ b.keySet).foldLeft(zero)((acc, k) => {
				acc.updated(k, vMonoid.op(a.getOrElse(k, vMonoid.zero),
					b.getOrElse(k, vMonoid.zero)
				))
			})
		}

		def zero = Map[K, V]()
	}

mapMergeMonoid作为一个组合子（combinator），通过整数相加monoid把Map里key 相同的值都加起来：

val smMonoid: Monoid[Map[String, Map[String, Int]]] =
	mapMergeMonoid(mapMergeMonoid(intAddMonoid))

val m1 = Map("o1" -> Map("i1" -> 1, "i2" -> 2))
val m2 = Map("o1" -> Map("i2" -> 3))
val m3 = smMonoid.op(m1, m2)
//> m3  : Map[String,Map[String,Int]] = Map(o1 -> Map(i1 -> 1, i2 -> 5))

容器为函数的例子：

def functionMonoid[A, B](B: Monoid[B]): Monoid[A => B] =
	new Monoid[A => B] {
		def op(f: A => B, g: A => B) = a => B.op(f(a), g(a))
		val zero: A => B = a => B.zero
	}

bag函数可以统计单词出现的数量：

def bag[A](as: IndexedSeq[A]): Map[A, Int] =
	foldMapV(
			as, mapMergeMonoid[A, Int](intAddMonoid)
	)((a: A) => Map(a -> 1))

bag("a rose is a rose")
//> Map(e -> 2, s -> 3, a -> 2, i -> 1,   -> 4, r -> 2, o -> 2)

bag(Vector("a", "rose", "is", "a", "rose"))
//> Map(a -> 2, rose -> 2, is -> 1)

使用monoid整合多个遍历

多个monoid可以组合成一个，这样就可以在一次折叠时同时执行多个操作。比如同时计算List的长度和值的总和：

首先把两个整数加法组对，因为，计数与求和都是整数加法操作：

val cvMonoid = productMonoid(intAddMonoid, intAddMonoid)
//> cvMonoid  : ch10.monoid.group.Monoid[(Int, Int)]

计数操作每次都是加1，所以写死值是1。
求和操作每次加的都是传进来的值a。

val pair = ge.ListFoldable.foldMap(
		1 :: 2 :: 3 :: 4 :: Nil
	)(a => (1, a))(cvMonoid)                //> pair  : (Int, Int) = (5,15)
                                                
pair._2.toDouble / pair._1                //> res38: Double = 3.0

范畴论

范畴论（category theory）在全局属性的层面概括了所有数学概念，所以它的B格很高，直冲天际。范畴论在高级函数式编程中占有中心位置，并被率先应用在Haskell中解决各种设计问题。

Scala中有一个实现了范畴的库Scalaz（发音为Scala Zed）。

范畴的基本概念

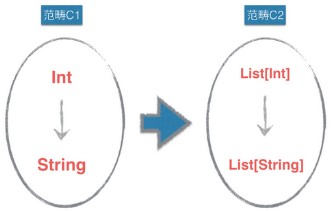
我们把范畴（category）看做一组类型及其关系态射（morphism）的集合。包括：

特定类型及其态射，比如Int、String、Int -> String；
高阶类型及其态射，比如List[Int]、List[String]、List[Int] -> List[String]。

态射

态射（morphism）也称为箭头（arrow）。它是对函数概念的一种推广，写为： \(f: A \mapsto B\)

对于每个态射\(f\)，其中一个对象为域（domain），另一个为值域（codomain）。对应到Scala中就是f: A => B。

例如下图介绍了一个简单的范畴：

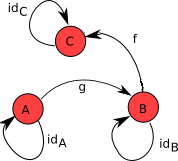
「对象」：该范畴由三个对像组成，分别为\(A\)、\(B\)、\(C\)。
「单位态射」：三个对象映射到自己，就是\(id_A\)、\(id_B\)、\(id_C\)。
「态射」：对象\(A\)到\(B\)中存在态射\(f: A \mapsto B\)、对象\(B\)到\(C\)中存在态射\(f: A \mapsto B\)

二元操作（射态的组合）

对于\(f: A \mapsto B\)和\(g: B \mapsto C\)，组合为\(g \circ f: A \mapsto C\)。

scala> val f1: Int => Int = i => i + 1
f1: Int => Int = <function1>

scala> val f2: Int => Int = i => i + 2
f2: Int => Int = <function1>

scala> val f3 = f1 compose f2
f3: Int => Int = <function1>

态射公理

范畴需要满足以下三个公理：

态射的组合操作要满足结合律。对于\(f: A \mapsto B\)，\(g: B \mapsto C\)，\(h: C \mapsto D\)，存在： \((f \circ g) \circ h = f \circ (g \circ h)\)
对任何一个范畴，其中任何一个对象\(A\)有且仅有一个单位态射\(id_A: A \mapsto A\) 。并且对于态射\(g：A \mapsto B\)有\(id_B \circ g = g = g \circ id_A\)。
态射在组合操作下是闭合的。所以如果存在态射\(f: A \mapsto B\)和\(g: B \mapsto C\)，那么范畴中必定存在态射\(h: A \mapsto C\)使得\(h = g \circ f\)。

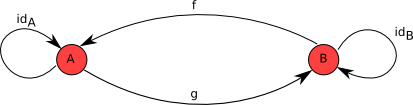
\(f\)和\(g\)都是态射，所以我们一定能够对它们进行组合并得到范畴中的另一个态射。那么哪一个是态射\(f \circ g\)呢？唯一的选择就是\(id_A\)了。类似地，\(g \circ f=id_B\)。

函子（Functor）

函数描述的是特定类型（Porper Type）之间的映射，而函子描述的是范畴（Category）之类的映射。

如果一个范畴内部的所有元素可以映射为另一个范畴的元素，且元素间的关系也可以映射为另一个范畴元素间关系，则认为这两个范畴之间存在映射。所谓函子就是表示两个范畴的映射。

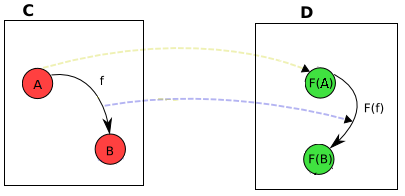
比如对于范畴\(C\)和\(D\)，对象之间的转换是用浅黄色的虚线箭头表示，态射之间的转换是用蓝紫色的箭头表示：

函子\(F : C \mapsto D\)能够：将\(C\)中任意对象\(A\)转换为\(D\)中的\(F(A)\);
将\(C\)中的态射\(f : A \mapsto B\)转换为\(D\)中的\(F(f) : F(A) \mapsto F(B)\)。

下图示范了一个更加复杂一点的例子，用\(F\)表示从范畴\(C\)到范畴\(D\)的函子：

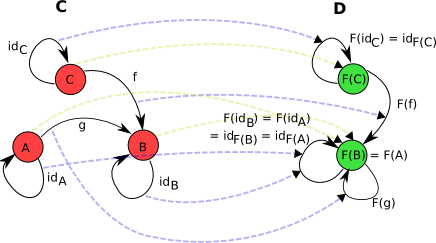
图中的文字描述了对象\(A\)和\(B\)被转换到了范畴\(D\)中同一个对象，因此，态射\(g\)就被转换成了一个源对象和目标对象相同的态射（不一定是单位态射），而且\(id_A\)和\(id_B\)变成了相同的态射。

用代码表示：

def map[A, B](o: Option[A])(f: A => B): Option[B] = ???
def map[A, B](o:   List[A])(f: A => B):   List[B] = ???
def map[A, B](o: Stream[A])(f: A => B): Stream[B] = ???

抽象为特质：

trait Functor[F[_]] {

	def map[A, B](fa: F[A])(f: A => B): F[B]
	
}

F[_]是参数化map的构造器，如同monoid里的Foldable。例如，用List：

val listFunctor = new Functor[List] {

	def map[A, B](as: List[A])(f: A => B): List[B] = as map f

}

对于F[(A, B)]，F是一个functor，可以定义distribute方法分派F到二元组，从而生成(F[A], F[B])。相当于一个更具泛用性的unzip操作，不仅适用于List，还可以应用到所有的functor上：

trait Functor[F[_]] {

	def map[A, B](fa: F[A])(f: A => B): F[B]

	def distribute[A, B](fab: F[(A, B)]): (F[A], F[B]) =
		(map(fab)(_._1), map(fab)(_._2))

}

listFunctor.distribute(("a", 1) :: ("b", 2) :: ("c", 3) :: Nil)
//> res0: (List[String], List[Int]) = (List(a, b, c),List(1, 2, 3))

trait Functor[F[_]] {

	def map[A, B](fa: F[A])(f: A => B): F[B]

	def distribute[A, B](fab: F[(A, B)]): (F[A], F[B]) =
		(map(fab)(_._1), map(fab)(_._2))

	def codistribute[A, B](e: Either[F[A], F[B]]): F[Either[A, B]] = e match {
		case Left(fa) => map(fa)(Left(_))
		case Right(fb) => map(fb)(Right(_))
	}

}

val er = new Right(1 :: 2 :: 3 :: Nil)    
//> er  : scala.util.Right[Nothing,List[Int]] = Right(List(1, 2, 3))
mf.listFunctor.codistribute(er)
//> res1: List[Either[Nothing,Int]] = List(Right(1), Right(2), Right(3))

val el = new Left("cannot divied by 0" :: "cannot divied by 0" :: Nil)
//> el  : scala.util.Left[List[String],Nothing] = Left(
//| List(cannot divied by 0, cannot divied by 0))
mf.listFunctor.codistribute(el)
//> res2: List[Either[String,Nothing]] = 
//| List(Left(cannot divied by 0), Left(can not divied by 0))

单位函子

对于每一个范畴\(C\)，都可以定义一个单位函子：\(Id: C \mapsto C\)。它将对象和态射直接转换成它们自己：\(Id[A] = A; f: A \mapsto B, Id[f] = f\)。

函子公理

给定一个对象\(A\)上的单位态射\(id_A\)，\(F(id_A)\)必须也是\(F(A)\)上的单位态射，也就是说：\(F(id_A) = id_{F(A)}\)
函子在态射组合上必须满足分配律，也就是说：\(F(f \circ g) = F(f) \circ F(g)\)

自函子

自函子（Endofunctor）是一类比较特殊的函子，它是一种将范畴映射到自身的函子 (A functor that maps a category to itself)。

函子这部分定义都很简单，但是理解起来会相对困难一些。如果范畴是一级抽象，那么函子就是二级抽象。起初我看函子的概念时，由于其定义简单，并且我很熟悉map这种操作，所以一带而过。当看到Monad时，发现了一些矛盾的地方。返回头再看，当初的理解是错误的。所以，在学习这部分概念时，个人有一些建议：

1. 函子是最基本，也是最重要的概念，这个要首先弄明白。本文后半部分有其代码实现，结合代码去理解。如何衡量已经明白其概念呢？脑补map的工作过程并且自己实现Functor。

2. 自函子也是我好长时间没有弄明白的概念。理解这个概念，可以参看Haskell关于Hask的定义。然后类比到Scala，这样会容易一些。

通过自函数（Endofunction）可以帮助理解自函子。函数identity是一个自函数的特例，它接收什么参数就返回什么参数，所以入参和返回值不仅类型一致，而且值也相同。

object Predef {
	// ...
	@inline def identity[A](x: A): A = x
	// ...
}

val arr = Array(1, 2, 3, 3, 3) //> arr  : Array[Int] = Array(1, 2, 3, 3, 3)
arr.groupBy(identity) //> Map(2 -> Array(2), 1 -> Array(1), 3 -> Array(3, 3, 3))

https://www.jianshu.com/p/31377066bf97

http://hongjiang.info/understand-monad-5-what-is-endofunctor/

https://www.jianshu.com/p/324c9ce77317

Monad：对flatMap和unit函数的泛化

只要实现了unit和flatMap就可以用map和map2方法了：

trait Functor[F[_]] {

	def map[A, B](fa: F[A])(f: A => B): F[B]

}

trait Monad[F[_]] extends Functor[F] {

	def unit[A](a: => A): F[A]

	def flatMap[A, B](ma: F[A])(f: A => F[B]): F[B]

	def map[A, B](ma: F[A])(f: A => B): F[B] =
		flatMap(ma)(a => unit(f(a)))
	
	def map2[A, B, C](ma: F[A], mb: F[B])(f: (A, B) => C): F[C] =
		flatMap(ma)(a => map(mb)(b => f(a, b)))
		

}

实现flatMap需要unit和flatMap：

val optionMonad = new Monad[Option] {

  def unit[A](a: => A) = Some(a)
  
  def flatMap[A,B](ma: Option[A])(f: A => Option[B]) = ma flatMap f
}

val streamMonad = new Monad[Stream] {

  def unit[A](a: => A) = Stream(a)
  
  def flatMap[A,B](ma: Stream[A])(f: A => Stream[B]) = ma flatMap f
}

val listMonad = new Monad[List] {

  def unit[A](a: => A) = List(a)
  
  def flatMap[A,B](ma: List[A])(f: A => List[B]) = ma flatMap f
}

引用scala.language.higherKinds包中的工具：

import scala.language.higherKinds

/**
 * 函子的抽像特质
 */
trait Functor[F[_]] { 
 def map[A, B](fa: F[A])(f: A => B): F[B]
}

Functor的作用是为容器中每个成员都映射出一个新的成员来：

范型定义为F[_]，表示它可以应用到成员为任何类型的容器。
A表示原来的类型，B表示新的类型。
map方法的参数fa: F[A]表示内容为A类型的源容器。
map方法的参数f: A => B表示把成员从A类型转为B类型的方法。
map方法的返回类型 F[B]表示返回值是内容为B类型的目标容器。

/**
 * `SeqF`实现了函子应用到容器类型为`Seq`的实现：
 */
object SeqF extends Functor[Seq] {
  def map[A, B](seq: Seq[A])(f: A => B): Seq[B] = seq map f
}

/**
 * `OptionF`实现了函子应用到容器类型为`Option`的实现：
 */
object OptionF extends Functor[Option] {
  def map[A, B](opt: Option[A])(f: A => B): Option[B] = opt map f
}

/**
 * `FunctionF`实现了函子应用到容器类型为`Function`的实现，
 * 把`A -> C`和`C -> B`两个函数转为一个新的函数`A -> B`：
 */
object FunctionF {
  def map[A, C, B](func: A => C)(f: C => B): A => B = {
    val functor = new Functor[({type L[D] = A => D})#L] {
      def map[E, B](func: A => E)(f: E => B): A => B =
        (a: A) => f(func(a))
    }
    functor.map(func)(f)
  }
}

调用：

val fii:    Int => Int    = i => 2 * i      //> fii  : Int    => Int
val fid:    Int => Double = i => 2.1 * i    //> fid  : Int    => Double
val fds: Double => String = d => d.toString //> fds  : Double => String

SeqF.map(List(1, 2, 3, 4))(fii)     //> res0: Seq[Int] = List(2, 4, 6, 8)
SeqF.map(List.empty[Int])(fii)      //> res1: Seq[Int] = List()
OptionF.map(Some(2))(fii)           //> res2: Option[Int] = Some(4)
OptionF.map(Option.empty[Int])(fii) //> res3: Option[Int] = None

val fa = FunctionF.map(fid)(fds)                      //> fa  : Int => String
val fb = FunctionF.map[Int, Double, String](fid)(fds) //> fb  : Int => String
val fc = fds compose fid                              //> fc  : Int => String
fa(2)                                     //> res4: String = 4.2
fb(2)                                     //> res5: String = 4.2
fc(2)                                     //> res6: String = 4.2