ch02 构造数据抽象 part02
层次性数据和闭包性质
组合数据对象的操作满足闭包性质:组合数据的结果还可以用同样的操作再进行组。
闭包性质可以实现层次性数据结构。形式:
(cons 1 2)
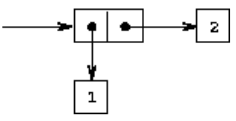
(cons (cons 1 2) (cons 3 4))

(cons (cons 1 (cons 2 3)) 4)
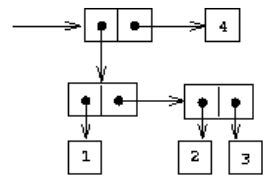
cons的闭包性质:序对中的元素也可以是序对。
序列的表示
(cons 1 (cons 2 (cons 3 (cons 4 nil))))
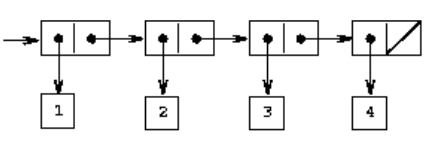
nil表示空表(拉丁文「nihil」,表示「什么也没有」)。
也可以简写为:
(list 1 2 3 4)
注意与:(1 2 3 4)的区别,它表示把参数2、3、4应用于过程1。
序列可以通过car与cdr取元素:
(define one-through-four (list 1 2 3 4)) (car one-through-four) ; 1 (cdr one-through-four) ; (2 3 4) (car (cdr one-through-four)) ; (10 1 2 3 4)
通过cons可以在表头上加上一个元素:
(cons 10 one-through-four) ; (5 1 2 3 4)
表操作
遍历列表
通过不断向下cdr遍历整个列表。取表中的第n个元素,算法:
-
n = 0,返回car -
递归调用自己,参数为
n - 1
(define (list-ref items n) (if (= n 0) (car items) (list-ref (cdr items) (- n 1))))
测试:
(define squares (list 1 4 9 16 25)) (list-ref squares 3) ; 16
检查列表是否为空
检查是否为空表,Scheme已经提供了内置的操作null?。
计算列表的长度
递归方式计算列表长度:
- 空表的length为0。
- 非空表的length就是这个表的cdr的\(length + 1\)
(define (length items) (if (null? items) 0 (+ 1 (length (cdr items))))) (define odds (list 1 3 5 7)) (length odds) ;; 4
迭代方式计算长度:
(define (length items) (define (length-iter a count) (if (null? a) count (length-iter (cdr a) (+ 1 count)))) (length-iter items 0))
拼接两个列表
递归方式实现append过程拼接两个表:
-
如果
list1为空,就返回list2 -
否则先用
(cdr list1)和list2进行append操作,然后再(car list1)的结果 cons加到结果的前面。
(define (append list1 list2) (if (null? list1) list2 (cons (car list1) (append (cdr list1) list2))))
练习 2.17 :取最后一个元素
取列表中最后一个元素。
last-pair需要处理以下三种情况:
- 空表:引发一个错误
- 单个元素的表:返回这个表本身
- 多于一个元素的表:继续向列表右边前进
以下是last-pair的定义:
;;; 17-last-pair.scm (define (last-pair lst) (cond ((null? lst) (error "list empty -- LAST-PAIR")) ((null? (cdr lst)) lst) (else (last-pair (cdr lst)))))
测试:
(load "17-last-pair.scm") (last-pair (list 1)) ; Value 12: (1) (last-pair (list 1 2 3)) ; Value 11: (3)
练习 2.18 :反转列表顺序
反转列表的顺序:
;;; 18-reverse.scm (define (reverse lst) (iter lst '())) (define (iter remained-items result) (if (null? remained-items) result (iter (cdr remained-items) (cons (car remained-items) result))))
reverse使用一个迭代过程iter来执行实际的逆序操作。
对于空表'(),iter只是简单地返回空表。
另一方面,如果输入表非空,那么iter就会以逆序的方式组合起输入列表,从而形成
一个逆序的列表。
比如说,对于列表(list 3 2 1)来说,iter先组合起(cons 1 '()),然后是
(cons 2 (cons 1 '())),最后是(cons 3 (cons 2 (cons 1'())))。
测试:
(load "18-reverse.scm") (reverse '()) ;Value: () (reverse (list 1 2 3)) ;Value 11: (3 2 1)
练习 2.19
改进1.2.2的兑换零钱程序,用一个列表可以定义可用的面值。如美元与英磅的面值不同, 就可以通过:
(define us-coins (list 50 25 10 5 1)) (define uk-coins (list 100 50 20 10 5 2 1 0.5)) (define (cc amount coin-values) (cond ((= amount 0) 1) ((or (< amount 0) (no-more? coin-values)) 0) (else (+ (cc amount (except-first-denomination coin-values)) (cc (- amount (first-denomination coin-values)) coin-values)))))
计算美元找零时:
(cc 100 us-coins)
答:以下是找零程序的其他函数:
;;; 19-other.scm (define (first-denomination coin-values) (car coin-values)) (define (except-first-denomination coin-values) (cdr coin-values)) (define (no-more? coin-values) (null? coin-values))
现在可以进行找零测试了:
(load "19-cc.scm") (load "19-other.scm") (define us-coins (list 50 25 10 5 1)) ;Value: us-coins (cc 100 us-coins) ;Value: 292 (define uk-coins (list 100 50 20 10 5 2 1 0.5)) ;Value: uk-coins (cc 100 uk-coins) ;Value: 104561
货币的排序并不会影响找零的结果,验证这一断言的最简单方法就是将一个逆序的货币
列表重新传入cc程序,可以看到计算的结果和之前未逆序的货币排列一样:
(cc 100 (reverse us-coins)) ;Value: 292 (cc 100 (reverse uk-coins)) ;Value: 104561
练习 2.20 :可变长参数列表
define、*、list这些方法的参数长度是不固定的。定义变长参数的方式是define
时参数列表中用.
如参数个数为2个以上:
(define (f x y . z) (display x) (display ",") (display y) (display ",") (display z))
调用时:
(f 1 2 3) ; 1,2,(3) (f 1 2) ; 1,2,() (f 1) ; error
以下定义了一个可以没有参数也可以有多个参数的方法:
(define (f . x) (display x)
定义一个有变长参数的过程,它返回和第一个参数奇偶性相同的其他参数:
same-parity函数要完成两件事:
- 检查第一个参数的奇偶性
- 检查所有参数,只保留奇偶性和第一个参数相同的那些参数
第一个任务可以用even?或者odd?函数来完成:
(even? 10) ;Value: #t (odd? 10) ;Value: #f
第二个任务则要求我们拥有对一个列表进行某种过滤的能力,filter函数可以完成这个
任务,它接受一个谓词函数和一个列表作为参数,并返回列表中那些谓词函数检测结果
为真的元素(filter函数在书本 78 页介绍):
(filter even? (list 1 2 3 4)) ;Value 12: (2 4) (filter zero? (list 1 0 2 0 3 0)) ;Value 13: (0 0 0)
以下是same-parity函数的定义:
;;; 20-same-parity.scm (define (same-parity sample . others) (filter (if (even? sample) even? odd?) (cons sample others))) ; 别忘了 sample 也要包含在列表内
测试:
(load "20-same-parity.scm") (same-parity 1) ;Value 11: (1) (same-parity 1 2 3 4 5 6 7) ;Value 14: (1 3 5 7) (same-parity 2 3 4 5 6 7) ;Value 15: (2 4 6)
对表的映射
Scheme内置的map方法
map第一个参数是一个接收n个参数的方法,其他的n个参数都是列表。 把方法应用在n个列表上。
(map + (list 1 2 3) (list 40 50 60) (list 700 800 900)) ;; (741 852 963)
(map (lambda (x y) (+ x (* 2 y))) (list 1 2 3) (list 4 5 6)) ;; (9 12 15)
自己实现一个map方法
map方法对表中的所有成员执行指定的操作。如,对表中每个成员做乘法:
(define (scale-list items factor)
(map
(lambda (x) (* x factor))
items))
把表中的每个成员乘10:
(scale-list (list 1 2 3 4 5) 10) ; Value 13: (10 20 30 40 50)
练习 2.21
定义过程返回表中每个元素的平方:
首先要给出的是使用cons定义的square-list,这个函数和书本 70 页的scale-list
函数很相似:
;;; 21-square-list-using-cons.scm (define (square-list items) (if (null? items) '() (cons (square (car items)) (square-list (cdr items)))))
测试:
(square-list (list 1 2 3 4)) ; Value 11: (1 4 9 16)
第二个square-list定义使用map函数,它和书本 71 页的scale-list函数很相似:
;;; 21-square-list-using-map.scm (define (square-list items) (map square items))
测试:
(square-list (list 1 2 3 4)) ; Value 11: (1 4 9 16)
练习 2.22
下面的过程试图用迭代的方式实现前面2.21的square-list过程,但为什么顺序反了?
(define (square-list items) (define (iter things answer) (if (null? things) answer (iter (cdr things) (cons (square (car things)) answer)))) (iter items nil))
使用(list 1 2 3 4)作为输入,测试square-list函数:
(load "22-square-list-by-louis.scm") (square-list (list 1 2 3 4)) ;Value 11: (16 9 4 1)
展开前面执行的表达式的运行序列:
(square-list (list 1 2 3 4)) (iter (list 1 2 3 4) '()) (iter (list 2 3 4) (cons (square 1) '())) (iter (list 3 4) (cons (square 2) '(1))) (iter (list 4) (cons (square 3) '(4 1))) (iter '() (cons (square 4) '(9 4 1))) '(16 9 4 1)
实际上,如果将square函数的调用去掉, Louis写出的其实就是练习 2.18 的reverse
函数:
;;; 18-reverse.scm (define (reverse lst) (iter lst '())) (define (iter remained-items result) (if (null? remained-items) result (iter (cdr remained-items) (cons (car remained-items) result))))
这也就说明了square-list生成逆序列表的原因。
为什么交换cons方法的参数以后顺序还是反的?
(define (square-list items) (define (iter things answer) (if (null? things) answer (iter (cdr things) (cons answer (square (car things)))))) (iter items nil))
将(list 1 2 3 4)作为输入,对square-list进行测试:
(load "22-another-square-list-by-louis.scm") (square-list (list 1 2 3 4)) ;Value 12: ((((() . 1) . 4) . 9) . 16)
可以看到,新的square-list产生的列表虽然顺序正确,但组合起来的方式不太对。
展开前面的表达式:
(square-list (list 1 2 3 4)) (iter (list 1 2 3 4) '()) (iter (list 2 3 4) (cons '() (square 1))) (iter (list 3 4) (cons (cons '() 1) (square 2))) (iter (list 4) (cons (cons (cons '() 1) 4) (square 3))) (iter '() (cons (cons (cons (cons '() 1) 4) 9) (square 4))) (iter '() (cons (cons (cons (cons '() 1) 4) 9) 16)) (cons (cons (cons (cons '() 1) 4) 9) 16)
可以看到square-list生成的并不是列表,而是一个使用cons组织起的序对序列,
它组织起元素的方式和位置都搞错了。
正确实现迭代计算square-list
其实 Louis 完全不必如此麻烦,只要对他的第一个square-list进行一点小修改,就
可以获得一个正确的、迭代计算的square-list实现:
;;; 22-iter-square-list.scm
(define (square-list items)
(define (iter things answer)
(if (null? things)
(reverse answer) ; 修改
(iter (cdr things)
(cons (square (car things))
answer))))
(iter items '()))
以上的square-list实现和 Louis 的第一个square-list实现几乎完全一样,
唯一不同的一行是,当输入列表为空时,iter先反序answer列表,然后才将它返回给
调用者,这样的话,原本逆序的结果列表又变为正序了,而且维持迭代计算方式不变。
测试:
(load "22-iter-square-list.scm") (square-list (list 1 2 3 4)) ; Value 11: (1 4 9 16)
迭代square-iter的另一种选择是,不在计算的最后逆序answer,而是在iter开始的
时候就将输入列表逆序,这样得出来的结果表在调用者看来就是正序的了:
;;; 22-another-iter-square-list.scm (define (square-list items) (define (iter things answer) (if (null? things) answer (iter (cdr things) (cons (square (car things)) answer)))) (iter (reverse items) '())) ; 修改
测试:
(load "22-another-iter-square-list.scm") (square-list (list 1 2 3 4)) ;Value 11: (1 4 9 16)
以上两种方法都会增加一次\(\Theta(n)\)复杂度的reverse调用,不过square-list的
总复杂度仍是\(\Theta(n)\)。
练习 2.23 :for-each遍历操作
定义一个和map过程类似的过程for-each,只是没有返回值。可以进行打印之类的操作
:
(for-each (lambda (x) (newline) (display x)) (list 57 321 88))
可以使用特殊形式begin加上if来定义for-each:
;;; 23-for-each-using-if.scm (define (for-each p lst) (if (not (null? lst)) (begin (p (car lst)) (for-each p (cdr lst)))))
测试:
(for-each (lambda (x) (newline) (display x)) (list 57 321 88)) 57 321 88 ;Unspecified return value
特殊形式begin可以确保多条表达式按顺序求值,它可以将多条表达式当作一条表达式
来运行,因此可以用在只支持单条表达式的if形式里。
另一种定义for-each的办法是使用cond:
;;; 23-another-for-each.scm
(define (for-each p lst)
(cond ((not (null? lst))
(p (car lst))
(for-each p (cdr lst)))))
测试:
(load "23-another-for-each.scm") (for-each (lambda (x) (newline) (display x)) (list 57 321 88)) 57 321 88 ;Unspecified return value
因为cond形式支持多条表达式,因此可以直接将两个表达式都放进cond形式之内(
实际上,cond的形式体内有一个隐式的begin)。
See also
关于if、cond和begin这三个特殊形式的更多信息,可以参考手册的
Special Form
章节 。
层次性结构
对于结构((1 2) 3 4)可以通过以下方式构造出来:
(cons (list 1 2) (list 3 4)) ; ((1 2) 3 4)
数据结构:

注意与(cons (cons 1 2) (cons 3 4))的区别:

层次结构:
再来看看其他的例子:
(cons (list 1 2 3) (list 4 5 6)) ;Value 13: ((1 2 3) 4 5 6) (list (list 1 2 3) (list 4 5 6) (list 7 8 9)) ;Value 14: ((1 2 3) (4 5 6) (7 8 9))
计算叶节点的数量
计算叶节点数量,要求的效果:
(define x (cons (list 1 2) (list 3 4))) (length x) ; 3 (count-leaves x) ; 4 (list x x) ; (((1 2) 3 4) ((1 2) 3 4)) (length (list x x)) ; 2 (count-leaves (list x x)) ; 8
递归计算时,树x的count-leaves应该是x的car的count-leaves与x的cdr的
count-leaves之和。而一个树叶的count-leaves为1。Scheme提供了基本过程pair?
可以检查其参数是否为序对。
(define (count-leaves x) (cond ((null? x) 0) ((not (pair? x)) 1) (else (+ (count-leaves (car x)) (count-leaves (cdr x))))))
练习 2.24
表达式(list 1 (list 2 (list 3 4)))的打印结果如下:
1 ]=> (list 1 (list 2 (list 3 4))) ;Value 11: (1 (2 (3 4)))
它的盒子图形如下:

它的树形图如下:

练习 2.25 :取出指定元素
使用car和cdr从以下列表中取出元素7。
首先是(1 3 (5 7) 9):
1 ]=> (define x (list 1 3 (list 5 7) 9)) ;Value: x 1 ]=> x ;Value 11: (1 3 (5 7) 9) 1 ]=> (cdr x) ;Value 12: (3 (5 7) 9) 1 ]=> (cddr x) ;Value 13: ((5 7) 9) 1 ]=> (caddr x) ;Value 14: (5 7) 1 ]=> (cdaddr x) ;Value 15: (7) 1 ]=> (car (cdaddr x)) ;Value: 7
然后是((7)):
1 ]=> (define y (list (list 7))) ;Value: y 1 ]=> y ;Value 16: ((7)) 1 ]=> (car y) ;Value 17: (7) 1 ]=> (caar y) ;Value: 7
最后是(1 (2 (3 (4 (5 (6 7)))))):
1 ]=> (define z (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 7))))))) ;Value: z 1 ]=> (cdr z) ;Value 24: ((2 (3 (4 (5 (6 7)))))) 1 ]=> (cadr z) ;Value 25: (2 (3 (4 (5 (6 7))))) 1 ]=> (cdadr z) ;Value 26: ((3 (4 (5 (6 7))))) 1 ]=> (cadadr z) ;Value 27: (3 (4 (5 (6 7)))) 1 ]=> (cdr (cadadr z)) ;Value 28: ((4 (5 (6 7)))) 1 ]=> (cadr (cadadr z)) ;Value 29: (4 (5 (6 7))) 1 ]=> (cdadr (cadadr z)) ;Value 30: ((5 (6 7))) 1 ]=> (cadadr (cadadr z)) ;Value 31: (5 (6 7)) 1 ]=> (cdr (cadadr (cadadr z))) ;Value 32: ((6 7)) 1 ]=> (cadr (cadadr (cadadr z))) ;Value 33: (6 7) 1 ]=> (cdadr (cadadr (cadadr z))) ;Value 34: (7) 1 ]=> (cadadr (cadadr (cadadr z))) ;Value: 7
练习 2.26
有两个列表x和y:
(define x (list 1 2 3)) (define y (list 4 5 6))
求以下表达式的打印结果:
(append x y) (cons x y) (list x y)
1 ]=> (append x y) ;Value 35: (1 2 3 4 5 6) (1 2 3 4 5 6) (2 3 4 5 6) (3 4 5 6) (4 5 6) (5 6) (6) [*]-------------> [*]------------> [*]---------> [*]--------> [*]-----> [*]---> nil | | | | | | v v v v v v 1 2 3 4 5 6
1 ]=> (cons x y) ;Value 36: ((1 2 3) 4 5 6) ((1 2 3) 4 5 6) (4 5 6) (5 6) (6) [*]---------------> [*]--------> [*]-------> [*]---> nil | | | | | v v v | 4 5 6 | | (1 2 3) (2 3) (3) [*]---------> [*]---------> [*]-----> nil | | | v v v 1 2 3
1 ]=> (list x y) ;Value 37: ((1 2 3) (4 5 6)) ((1 2 3) (4 5 6)) ((4 5 6)) [*]------------------> [*]------------> nil | | | | | | (4 5 6) (5 6) (6) | [*]----------> [*]------> [*]---> nil | | | | | v v v | 4 5 6 | | (1 2 3) (2 3) (3) [*]----------> [*]--------> [*]----> nil | | | v v v 1 2 3
练习 2.27 :反转树与子树
修改练习2.18中的reverse过程为deep-reverse,能把表的子表元素也反转:
deep-reverse函数比reverse函数更进一步,它不仅逆序最外层的列表(树根),而且
还使用递归,连内层的子树也一并进行逆序。
;;; 27-deep-reverse.scm (define (deep-reverse tree) (cond ((null? tree) '()) ; 空树 ((not (pair? tree)) tree) ; 叶子 (else ; 递归地逆序左右子树 (reverse (list (deep-reverse (car tree)) (deep-reverse (cadr tree)))))))
测试:
1 ]=> (load "27-deep-reverse.scm") ;Loading "27-deep-reverse.scm"... done ;Value: deep-reverse 1 ]=> (define x (list (list 1 2) (list 3 4))) ;Value: x 1 ]=> x ;Value 11: ((1 2) (3 4)) 1 ]=> (reverse x) ;Value 12: ((3 4) (1 2)) 1 ]=> (deep-reverse x) ;Value 13: ((4 3) (2 1))
better-deep-reverse
通过使用一些辅助函数,可以让deep-reverse程序更具可读性:
;;; 27-better-deep-reverse.scm (define (deep-reverse tree) (cond ((empty-tree? tree) '()) ((leaf? tree) tree) (else (reverse (make-tree (deep-reverse (left-branch tree)) (deep-reverse (right-branch tree))))))) (define (empty-tree? tree) (null? tree)) (define (leaf? tree) (not (pair? tree))) (define (make-tree left-branch right-branch) (list left-branch right-branch)) (define (left-branch tree) (car tree)) (define (right-branch tree) (cadr tree))
测试:
1 ]=> (load "27-better-deep-reverse.scm") ;Loading "27-better-deep-reverse.scm"... done ;Value: right-branch 1 ]=> (define x (list (list 1 2) (list 3 4))) ;Value: x 1 ]=> x ;Value 11: ((1 2) (3 4)) 1 ]=> (reverse x) ;Value 12: ((3 4) (1 2)) 1 ]=> (deep-reverse x) ;Value 13: ((4 3) (2 1))
tree-reverse
上面两个函数只能处理输入为二叉树的情况, 也即是,对于像
(list (list 1 2) (list 3 4))这样的输入,deep-reverse和better-deep-reverse
可以给出正确的输出, 但是,如果输入不是二叉树,那么它们的输出就不是正确的:
;; 输入为三叉树,正确输出应该是 ((6 5) (4 3) (2 1)) 才对 1 ]=> (deep-reverse (list (list 1 2) (list 3 4) (list 5 6))) ;Value 11: ((4 3) (2 1))
以下函数可以处理输入不为二叉树的情况:
;;; 27-tree-reverse.scm (define (tree-reverse lst) (define (iter remained-items result) (if (null? remained-items) result (iter (cdr remained-items) (cons (if (pair? (car remained-items)) (tree-reverse (car remained-items)) (car remained-items)) result)))) (iter lst '()))
无论输入是二叉树、三叉树,等等,这个函数都可以给出正确的输出:
1 ]=> (load "27-tree-reverse.scm") ;Loading "27-tree-reverse.scm"... done ;Value: tree-reverse 1 ]=> (tree-reverse (list (list 1 2) (list 3 4))) ;Value 11: ((4 3) (2 1)) 1 ]=> (tree-reverse (list (list 1 2) (list 3 4) (list 5 6))) ;Value 12: ((6 5) (4 3) (2 1))
练习 2.28:树转为列表
实现过程fringe,作用是把树按从左到右输出为列表。例:
(define x (list (list 1 2) (list 3 4))) (fringe x) ; Value: (1 2 3 4) (fringe (list x x)) ; Value: (1 2 3 4 1 2 3 4)
要遍历一棵树并累积它的所有元素,我们会遇到以下三种情况:
-
元素是空表,也即是空树,返回
'() -
元素是单个节点(不是序对),也即是叶子节点,对它使用
list函数,让它变成一个 只有单个元素的列表 -
元素有左右两棵子树,使用书本 68 页提到的
append过程(MIT Scheme 也内置了这个 过程),对两棵子树的所有元素进行累积
;;; 28-fringe.scm (define (fringe tree) (cond ((null? tree) '()) ; 空树 ((not (pair? tree)) (list tree)) ; 叶子 (else (append (fringe (car tree)) ; 累积左子树所有元素 (fringe (cadr tree)))))) ; 累积右子树所有元素
测试:
1 ]=> (load "28-fringe.scm") ;Loading "28-fringe.scm"... done ;Value: fringe 1 ]=> (define x (list (list 1 2) (list 3 4))) ;Value: x 1 ]=> (fringe x) ;Value 13: (1 2 3 4) 1 ]=> (fringe (list x x)) ;Value 14: (1 2 3 4 1 2 3 4)
可以通过增加一些辅助函数,来让fringe函数的定义更具可读性:
;;; 28-better-fringe.scm (define (fringe tree) (cond ((empty-tree? tree) '()) ((leaf? tree) (list tree)) (else (append (fringe (left-branch tree)) (fringe (right-branch tree)))))) (define (empty-tree? tree) (null? tree)) (define (leaf? tree) (not (pair? tree))) (define (left-branch tree) (car tree)) (define (right-branch tree) (cadr tree))
对fringe进行测试:
1 ]=> (load "28-better-fringe.scm") ;Loading "28-better-fringe.scm"... done ;Value: right-branch 1 ]=> (define x (list (list 1 2) (list 3 4))) ;Value: x 1 ]=> (fringe x) ;Value 15: (1 2 3 4) 1 ]=> (fringe (list x x)) ;Value 16: (1 2 3 4 1 2 3 4)
评论
不應該用car,cdr就可以了,否則只對二叉樹有效。另外即使改成cdr后還有問題,
如果樹中的葉子有nil的話,nil在最後的結果中會消失,改用如下版本可以消除
這兩個問題:
;; exercise 2.28 (define (fringe tree) (define (fringe-car tree) (if (not (pair? tree)) (list tree) (fringe tree))) (if (null? tree) tree (append (fringe-car (car tree)) (fringe (cdr tree)))))
练习 2.29
二叉活动体:端上可以挂重量,也可以是另一个二叉活动体。分支的杆长度确定。
用复合数据表示:通过两个分支构造起来:
(define (make-mobile left right) (list left right))
分支长度为length,端点上的重量或另一个分支为structure:
(define (make-branch length structure) (list length structure))
a) 实现left-branch函数和right-branch函数
实现left-branch函数和right-branch函数分别返回两个分支。还有branch-length
和branch-structure返回分支的上一部分。
根据以上定义,先写出对应的left-branch和right-branch:
;;; 29-left-branch-and-right-branch.scm (define (left-branch mobile) (car mobile)) (define (right-branch mobile) (cadr mobile))
然后是对应的branch-length和branch-structure:
;;; 29-branch-length-and-branch-structure.scm (define (branch-length branch) (car branch)) (define (branch-structure branch) (cadr branch))
为了使用的方便,将以上三个文件放进一个文件里面:
;;; 29-mobile-reppresent.scm (load "29-make-mobile-and-make-branch.scm") (load "29-left-branch-and-right-branch.scm") (load "29-branch-length-and-branch-structure.scm")
然后进行测试:
1 ]=> (load "29-mobile-represent.scm") ;Loading "29-mobile-represent.scm"... ; Loading "29-make-mobile-and-make-branch.scm"... done ; Loading "29-left-branch-and-right-branch.scm"... done ; Loading "29-branch-length-and-branch-structure.scm"... done ;... done ;Value: branch-structure 1 ]=> (define mobile (make-mobile (make-branch 10 25) (make-branch 5 20))) ;Value: mobile 1 ]=> (left-branch mobile) ;Value 11: (10 25) 1 ]=> (right-branch mobile) ;Value 12: (5 20) 1 ]=> (branch-length (right-branch mobile)) ;Value: 5 1 ]=> (branch-structure (right-branch mobile)) ;Value: 20
b) total-weight 函数
b) 定义total-weight,返回一个活动体的总重量
通过分析题目,可以得出计算一个活动体重量所需的两条规则:
- 对于一个活动体来说,它的总重量就是这个活动体的左右两个分支的重量之和。
-
对于一个分支来说,如果这个分支的
structure部分是一个数,那么这个数就是这个 分支的重量;另一方面,如果这个分支的 structure 部分指向另一个活动体,那么 这个活动体的总重量就是这个分支的重量。
根据上面的两条规则,现在可以给出total-weight函数的定义了:
;;; 29-total-weight.scm (load "29-left-branch-and-right-branch.scm") (load "29-branch-length-and-branch-structure.scm") (define (total-weight mobile) (+ (branch-weight (left-branch mobile)) ; 计算左右两个分支的重量之和 (branch-weight (right-branch mobile)))) (define (branch-weight branch) (if (hangs-another-mobile? branch) ; 如果分支吊着另一个活动体 (total-weight (branch-structure branch)) ; 那么这个活动体的总重量就是这个分支的重量 (branch-structure branch))) ; 否则, 分支的 structure 部分就是分支的重量 (define (hangs-another-mobile? branch) ; 检查分支是否吊着另一个活动体 (pair? (branch-structure branch)))
测试:
1 ]=> (load "29-mobile-represent.scm")
;Loading "29-mobile-represent.scm"...
; Loading "29-make-mobile-and-make-branch.scm"... done
; Loading "29-left-branch-and-right-branch.scm"... done
; Loading "29-branch-length-and-branch-structure.scm"... done
;... done
;Value: branch-structure
1 ]=> (load "29-total-weight.scm")
;Loading "29-total-weight.scm"...
; Loading "29-left-branch-and-right-branch.scm"... done
; Loading "29-branch-length-and-branch-structure.scm"... done
;... done
;Value: hangs-another-mobile?
1 ]=> (define mobile (make-mobile (make-branch 10 20) ; 活动体的总重量为 20 + 25 = 45
(make-branch 10 25)))
;Value: mobile
1 ]=> (total-weight mobile)
;Value: 45
1 ]=> (define another-mobile (make-mobile (make-branch 10 mobile) ; 左分支吊着另一个活动体,总重为 45
(make-branch 10 20))) ; 右分支的重量是 20
;Value: another-mobile
1 ]=> (total-weight another-mobile)
;Value: 65
c) 检查活动体是否平衡
一个平衡的活动体需要满足以下两个条件:
- 这个活动体左右两个分支的力矩相等
- 这个活动体左右两个分支上的所有子活动体(如果有的话)也都平衡
很明显,要判断一个活动体是否平衡,我们不仅要检查给定的活动体,还要递归地检查 给定活动体的所有子活动体才行。
首先,写出计算分支力矩的程序,这要用到前面定义的branch-weight:
;;; 29-branch-torque.scm
(load "29-branch-length-and-branch-structure.scm") ; 载入 branch-length
(load "29-total-weight.scm") ; 载入 branch-weight
(define (branch-torque branch)
(* (branch-length branch)
(branch-weight branch)))
测试力矩程序:
1 ]=> (load "29-branch-torque.scm") ;Loading "29-branch-torque.scm"... ; Loading "29-branch-length-and-branch-structure.scm"... done ; Loading "29-total-weight.scm"... ; Loading "29-left-branch-and-right-branch.scm"... done ; Loading "29-branch-length-and-branch-structure.scm"... done ; ... done ;... done ;Value: branch-torque 1 ]=> (load "29-make-mobile-and-make-branch.scm") ;Loading "29-make-mobile-and-make-branch.scm"... done ;Value: make-branch 1 ]=> (define branch (make-branch 10 20)) ;Value: branch 1 ]=> (branch-torque branch) ;Value: 200
有了力矩计算程序之后,就可以写检查平衡的程序的了:
;;; 29-mobile-balance.scm
(load "29-left-branch-and-right-branch.scm") ; 载入 left-branch 和 right-branch
(load "29-branch-length-and-branch-structure.scm") ; 载入 branch-structure
(load "29-branch-torque.scm") ; 载入 branch-torque
(define (mobile-balance? mobile)
(let ((left (left-branch mobile))
(right (right-branch mobile)))
(and ; 必须同时满足以下三个条件,才是平衡的活动体
(same-torque? left right)
(branch-balance? left)
(branch-balance? right))))
(define (same-torque? left right)
(= (branch-torque left)
(branch-torque right)))
(define (branch-balance? branch)
(if (hangs-another-mobile? branch) ; 如果分支上有子活动体
(mobile-balance? (branch-structure branch)) ; 那么(递归地)检查子活动体的平衡性
#t)) ; 否则,返回 #t
测试:
1 ]=> (load "29-mobile-balance.scm")
;Loading "29-mobile-balance.scm"...
; Loading "29-left-branch-and-right-branch.scm"... done
; Loading "29-branch-length-and-branch-structure.scm"... done
; Loading "29-branch-torque.scm"...
; Loading "29-branch-length-and-branch-structure.scm"... done
; Loading "29-total-weight.scm"...
; Loading "29-left-branch-and-right-branch.scm"... done
; Loading "29-branch-length-and-branch-structure.scm"... done
; ... done
; ... done
;... done
;Value: branch-balance?
1 ]=> (load "29-mobile-represent.scm")
;Loading "29-mobile-represent.scm"...
; Loading "29-make-mobile-and-make-branch.scm"... done
; Loading "29-left-branch-and-right-branch.scm"... done
; Loading "29-branch-length-and-branch-structure.scm"... done
;... done
;Value: branch-structure
1 ]=> (define balance-mobile (make-mobile (make-branch 10 10)
(make-branch 10 10)))
;Value: balance-mobile
1 ]=> (mobile-balance? balance-mobile) ;Value: #t
1 ]=> (define unbalance-mobile (make-mobile (make-branch 0 0)
(make-branch 10 10)))
;Value: unbalance-mobile
1 ]=> (mobile-balance? unbalance-mobile) ;Value: #f
1 ]=> (define mobile-with-sub-mobile (make-mobile (make-branch 10 balance-mobile)
(make-branch 10 balance-mobile)))
;Value: mobile-with-sub-mobile
1 ]=> (mobile-balance? mobile-with-sub-mobile) ;Value: #t
d) 新的表示方式
如果用新的形式定义结构体:
(define (make-mobile left right) (cons left right)) (define (make-branch length structure) (cons length structure))
要怎么修改现有的代码。
我们的活动体程序通过实现数据抽象的方式,将程序之间的关系很好地用构造函数和
选择函数隔离开了,就算make-mobile和make-branch这两个构造函数使用新的
表示方式,我们只需修改相应的选择函数,就可以让mobile-balance?等程序继续
运行在新表示之下。
需要修改的选择程序有left-branch、right-branch、branch-length和
branch-structure四个:
;;; 29-new-selector.scm (define (left-branch mobile) (car mobile)) (define (right-branch mobile) (cdr mobile)) (define (branch-length branch) (car branch)) (define (branch-structure branch) (cdr branch))
使用mobile-balance?函数来测试新的活动体表示:
1 ]=> (load "29-mobile-balance.scm")
;Loading "29-mobile-balance.scm"...
; Loading "29-left-branch-and-right-branch.scm"... done
; Loading "29-branch-length-and-branch-structure.scm"... done
; Loading "29-branch-torque.scm"...
; Loading "29-branch-length-and-branch-structure.scm"... done
; Loading "29-total-weight.scm"...
; Loading "29-left-branch-and-right-branch.scm"... done
; Loading "29-branch-length-and-branch-structure.scm"... done
; ... done
; ... done
;... done
;Value: branch-balance?
1 ]=> (load "29-new-selector.scm")
;Loading "29-new-selector.scm"... done
;Value: branch-structure
1 ]=> (load "29-new-constructor.scm")
;Loading "29-new-constructor.scm"... done
;Value: make-branch
1 ]=> (define mobile (make-mobile (make-branch 10 20)
(make-branch 10 20)))
;Value: mobile
1 ]=> mobile ; 确认使用的是新表示
;Value 11: ((10 . 20) 10 . 20)
1 ]=> (mobile-balance? mobile) ; 不必修改其他程序,就可以直接使用
;Value: #t
对树的映射
map与递归的组合是处理树的一种强有力的抽象。
可以用和count-leaves类似的递归方案,把树里的每个元素都乘上值:
(define (scale-tree tree factor) (cond ((null? tree) nil) ((not (pair? tree)) (* tree factor)) (else (cons (scale-tree (car tree) factor) (scale-tree (cdr tree) factor))))) (scale-tree (list 1 (list 2 (list 3 4) 5) (list 6 7)) 10) ;Value (10 (20 (30 40) 50) (60 70))
另一方案,把树视为子树的序列,并用map进行映射,依次对每棵子树做缩放:
(define (scale-tree tree factor) (map (lambda (sub-tree) (if (pair? sub-tree) (scale-tree sub-tree factor) (* sub-tree factor))) tree))
练习 2.30
实现square-tree,平方每个元素。
类似于练习 2.21的两种不同的square-list定义,我们也可以用两种不同的方式来定义
square-tree。
定义一
首先是使用cond判断的方式(这个函数和书本 75 的第一个scala-tree定义也很相似):
;;; 30-square-tree-using-cond.scm
(define (square-tree tree)
(cond ((null? tree) ; 空树
'())
((not (pair? tree)) ; 叶子节点
(square tree))
(else
(cons (square-tree (car tree))
(square-tree (cdr tree))))))
测试:
1 ]=> (square-tree (list (list 1 2) (list 3 4))) ;Value 11: ((1 4) (9 16))
定义二
然后是使用map遍历的方式(这个函数和书本 75 的第二个scala-tree定义也很相似)
:
;;; 30-square-tree-using-map.scm
(define (square-tree tree)
(map (lambda (sub-tree)
(if (pair? sub-tree) ; 如果有左右子树
(square-tree sub-tree) ; 那么递归地处理它们
(square sub-tree)))
tree))
测试:
1 ]=> (square-tree (list (list 1 2) (list 3 4))) ;Value 11: ((1 4) (9 16))
公共的抽象模式
可以看出,上面的两个square-tree函数共享着同样一种抽象模式,我们可以将这种
抽象模式抽取出来,作为一个单独的函数,具体请看练习 2.31 。
练习 2.31
进一步抽象练习 2.30的答案,使其可以实现以下的形式:
(define (square-tree tree) (tree-map square tree))
练习 2.30 的两个square-tree都共享同一种抽象模式,我们可以将这种模式单独
抽取出来,称之为tree-map。
和square-tree类似,tree-map也可以用两种不同的方式来定义。
定义一
;;; 31-tree-map-using-cond.scm (define (tree-map f tree) (cond ((null? tree) '()) ; 空树 ((not (pair? tree)) (f tree)) ; 叶子节点 (else (cons ; 递归处理左右子树 (tree-map f (car tree)) (tree-map f (cdr tree))))))
测试:
1 ]=> (tree-map square (list (list 1 2) (list 3 4))) ;Value 11: ((1 4) (9 16))
定义二
;;; 31-tree-map-using-map.scm
(define (tree-map f tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(tree-map f sub-tree) ; 处理子树
(f sub-tree))) ; 处理节点
tree))
测试:
1 ]=> (tree-map square (list (list 1 2) (list 3 4))) ;Value 11: ((1 4) (9 16))
练习 2.32
算出集合的所有子集,比如(1 2 3)的所有子集的集合就是:
(() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))
完整的程序定义如下:
;;; 32-subsets.scm (define (subsets s) (if (null? s) (list '()) (let ((rest (subsets (cdr s)))) (append rest (map (lambda (x) (cons (car s) x)) rest)))))
测试:
1 ]=> (load "32-subsets.scm") ;Loading "32-subsets.scm"... done ;Value: subsets 1 ]=> (subsets (list 1 2 3)) ;Value 11: (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))
这个过程的原理和之前的找零程序的原理是一样的,任何一本组合数学方面的书都能找到 相关的资料。
集合S的子集是(cdr S)的子集加上对(cdr S)里每个元素append上(car S)。
以题目中的例子来看,要求(1,2,3)的子集,先看(cdr S)的子集,也就是
(( ) (2) (3) (2 3))。然后再此基础上,给每个元素append上(car S),(car S)
就是1,所以得到((1) (1 2) (1 3) (1 2 3)),最后加这两个list连起来就得到
(1,2,3)子集了。
序列作为一种约定的界面
以序列作为统一的表示结构,就可以把程序对于数据结构的依赖局限到少数几个序列操作上 。可以方便地在不同表示之间转换。
例如,以下两个程序都有着相同的流程:
- 枚举器生成值。
- 过滤器过滤过符合的值。
- 转换器通过「映射」的方法处理每个值。
- 累积器把每个结果组合起来。
程序1:计算值为奇数的叶结点的平方和:
(define (sum-odd-squares tree)
(cond ((null? tree) 0)
((not (pair? tree))
(if (odd? tree) (square tree) 0))
(else (+ (sum-odd-squares (car tree))
(sum-odd-squares (cdr tree))))))
过程:
- 枚举树的叶结点
- 过滤出奇数
- 平方
- 累加
程序2:偶数斐波那契\(Fib(k)\),\(k < n\):
(define (even-fibs n)
(define (next k)
(if (> k n)
nil
(let ((f (fib k)))
(if (even? f)
(cons f (next (+ k 1)))
(next (+ k 1))))))
(next 0))
过程:
- 枚举\(0\)到\(n\)的整数
- 计算这些整数的斐波那契数
- 过滤,选出偶数
-
用
cons累积结果,从空表开始
可以看到两个过程的模式相同:
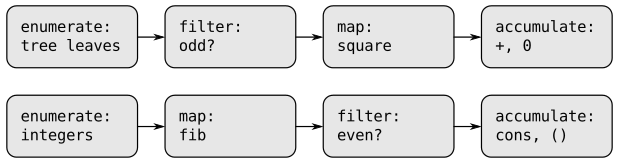
如果可以灵活地重新组织的话,就可以提高程序的清晰度。
序列操作
过滤列表
抽象出过滤操作,即选出满足某个谓词的元素。Scheme中已经有现成的filter过程了。
如果我们要自己实现一个的话,可以用这样的实现:
(define (filter predicate sequence)
(cond ((null? sequence) nil)
((predicate (car sequence))
(cons (car sequence)
(filter predicate (cdr sequence))))
(else (filter predicate (cdr sequence)))))
(filter odd? (list 1 2 3 4 5)) ;: (1 3 5)
累计结果
定义accumulate过程来实现累积操作:
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))
例子:用不同的方法累积:
(accumulate + 0 (list 1 2 3 4 5)) ;: 15 (accumulate * 1 (list 1 2 3 4 5)) ;: 120 (accumulate cons nil (list 1 2 3 4 5)) ;: (1 2 3 4 5)
生成整数序列
过程enumerate-interval生成指定区间中整数的序列:
(define (enumerate-interval low high) (if (> low high) nil (cons low (enumerate-interval (+ low 1) high))))
调用例子:
(enumerate-interval 2 7) ;: 从2到7的范围内
树中所有节点的序列
枚举树中所有的叶结点:
(define (enumerate-tree tree)
(cond ((null? tree) nil)
((not (pair? tree)) (list tree))
(else (append (enumerate-tree (car tree))
(enumerate-tree (cdr tree))))))
调用的例子
;: (enumerate-tree (list 1 (list 2 (list 3 4)) 5)) ;: (1 2 3 4 5)
重构
重构sum-odd-squares:
(define (sum-odd-squares tree)
(accumulate +
0
(map square
(filter odd?
(enumerate-tree tree)))))
重构even-fibs:
(define (even-fibs n)
(accumulate cons
nil
(filter even?
(map fib
(enumerate-interval 0 n)))))
这样模块化的流程可以在其他的程序里重用。例如,可以在构造前\(n + 1\)个斐波那契数 的平方和程序中使用之前写过的程序片段:
(define (list-fib-squares n)
(accumulate cons
nil
(map square
(map fib
(enumerate-interval 0 n)))))
(list-fib-squares 10) ;: (0 1 1 4 9 25 64 169 441 1156 3025)
也可以重新组织片段,生成所有奇数平方之乘积:
(define (product-of-squares-of-odd-elements sequence)
(accumulate *
1
(map square
(filter odd? sequence))))
(product-of-squares-of-odd-elements (list 1 2 3 4 5)) ;: 225
序列操作还可以增加逻辑,比如原来有一个从员工列表中找最高工资的程序,现在改成 找工资最高的程序员:
(define (salary-of-highest-paid-programmer records)
(accumulate max
0
(map salary
(filter programmer? records))))
总结:这里以序列作为统一表示结构,就可以把程序对于数据结构的依赖性局限到最少的 几个操作上,并保持整个设计不变。
练习 2.33
完成填空:
(define (map p sequence) (accumulate (lambda (x y) <??>) nil sequence)) (define (append seq1 seq2) (accumulate cons <??> <??>)) (define (length sequence) (accumulate <??> 0 sequence))
答:
通过研究各个目标函数的定义,可以得出使用accumulate实现这些函数的方式。
map
map原本的定义为:
;;; p70-map.scm
(define (map p sequence)
(if (null? sequence)
'()
(cons (p (car sequence))
(map p (cdr sequence)))))
而题目给出的accumulate定义的map的定义为:
(define (map p sequence)
(accumulate (lambda (x y) <??>)
'()
sequence))
通过展开对(accumulate (lambda (x y) <??>) '() sequence)调用,可以得出以下
表达式:
(if (null? sequence)
'()
((lambda (x y) <??>)
(car sequence)
(accumulate (lambda (x y) <??>)
'()
sequence)))
通过将这个展开式和原本map的定义对比可以看出,我们只要让(lambda (x y) <??>)
中的<??>的作用等同于(cons (p x) y)即可,因此,这个答案的解为
(lambda (x y) (cons (p x) y))。
以下是完整的map定义:
;;; 33-map.scm
(load "p78-accumulate.scm")
(define (map p sequence)
(accumulate (lambda (x y)
(cons (p x) y))
'()
sequence))
以下是求值(map square (list 1 2 3))时的展开式:
(map square (list 1 2 3))
(accumulate (lambda (x y) (cons (square x) y))
'()
(list 1 2 3))
(cons (square 1)
(accumulate (lambda (x y) (cons (square x) y))
'()
(list 2 3)))
(cons (square 1)
(cons (square 2)
(accumulate (lambda (x y) (cons (square x) y))
'()
(list 3))))
(cons (square 1)
(cons (square 2)
(cons (square 3)
(accumulate (lambda (x y) (cons (square x) y))
'()
'()))))
(cons (square 1)
(cons (square 2)
(cons (square 3)
'())))
(cons 1
(cons 4
(cons 9
'())))
(list 1 4 9)
测试:
1 ]=> (load "33-map.scm") ;Loading "33-map.scm"... ; Loading "p78-accumulate.scm"... done ;... done ;Value: map 1 ]=> (map square (list 1 2 3 4)) ;Value 11: (1 4 9 16)
append
以下是书本 68 页给出的append函数的定义:
;;; p68-append.scm
(define (append list1 list2)
(if (null? list1)
list2
(cons (car list1)
(append (cdr list1) list2))))
可以看到,append逐步遍历和重组整个list1,当list1处理完之后,将list2
连接到list1最后一个序对的cdr部分。
根据同样原理,使用accumulate实现的append的定义如下:
;;; 33-append.scm
(load "p78-accumulate.scm")
(define (append seq1 seq2)
(accumulate cons seq2 seq1))
以下是求值(append (list 1 2 3) (list 4 5 6))时的展开式:
(append (list 1 2 3) (list 4 5 6))
(accumulate cons (list 1 2 3) (list 4 5 6))
(cons 1
(accumulate cons (list 2 3) (list 4 5 6)))
(cons 1
(cons 2
(accumulate cons (list 3) (list 4 5 6))))
(cons 1
(cons 2
(cons 3
(accumulate cons '() (list 4 5 6)))))
(cons 1
(cons 2
(cons 3
(list 4 5 6))))
(list 1 2 3 4 5 6)
测试:
1 ]=> (load "33-append.scm") ;Loading "33-append.scm"... ; Loading "p78-accumulate.scm"... done ;... done ;Value: append 1 ]=> (append (list 1 2 3) (list 4 5 6)) ;Value 11: (1 2 3 4 5 6)
length
以下是书本 68 页给出的length函数的定义:
;;; p68-length.scm
(define (length items)
(if (null? items)
0
(+ 1
(length (cdr items)))))
length逐个遍历给定列表的元素,并将每个元素计数为 1 。
根据同样原理,使用accumulate实现的length的定义如下:
;;; 33-length.scm
(load "p78-accumulate.scm")
(define (length sequence)
(accumulate (lambda (x y) (+ 1 y))
0
sequence))
以下是求值(length (list 1 2 3))时的展开式:
(length (list 1 2 3))
(accumulate (lambda (x y) (+ 1 y))
0
(list 1 2 3))
(+ 1
(accumulate (lambda (x y) (+ 1 y))
0
(list 2 3)))
(+ 1
(+ 1
(accumulate (lambda (x y) (+ 1 y))
0
(list 3))))
(+ 1
(+ 1
(+ 1
(accumulate (lambda (x y) (+ 1 y))
0
'()))))
(+ 1
(+ 1
(+ 1
0)))
3
测试:
1 ]=> (load "33-length.scm") ;Loading "33-length.scm"... ; Loading "p78-accumulate.scm"... done ;... done ;Value: length 1 ]=> (length '()) ;Value: 0 1 ]=> (length (list 1 2 3)) ;Value: 3
练习 2.34
多项式:
\[ \begin{equation} \begin{split} a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0 \end{split} \end{equation} \]根据 Horner 规则可以转换成:
\[ \begin{equation} \begin{split} (\cdots (a_nx + a_{n-1})x + \cdots + a_1)x + a_0 \end{split} \end{equation} \]根据 Horner 规则,算式\(1 + 3x + 5x^3 + x^5\)可以转换成:
\[ \begin{equation} \begin{split} 1 + x(3 + x(0 + x(5 + x(0 + x)))) \end{split} \end{equation} \]以上算式又可以转换为相应的前序表示:
\[ \begin{equation} \begin{split} (+ 1 (* x (+ 3 (* x (+ 0 (* x (+ 5 (* x (+ 0 x))))))))) \end{split} \end{equation} \]
现在假设horner-eval函数可以正常运行的话,那么求值表达式
(horner-eval 2 (list 1 3 0 5 0 1))
应该会产生以下计算序列:
(horner-eval 2 (list 1 3 0 5 0 1))
(accumulate (lambda (this-coeff higher-terms) <??>)
0
(list 1 3 0 5 0 1))
(+ 1 (* 2
(accumulate (lambda (this-coeff higher-terms) <??>)
0
(list 3 0 5 0 1))))
(+ 1 (* 2
(+ 3 (* 2 (accumulate (lambda (this-coeff higher-terms) <??>)
0
(list 0 5 0 1))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2 (accumulate (lambda (this-coeff higher-terms) <??>)
0
(list 5 0 1))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2 (accumulate (lambda (this-coeff higher-terms) <??>)
0
(list 0 1))))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2
(+ 0 (* 2
(accumulate (lambda (this-coeff higher-terms) <??>)
0
(list 1))))))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2
(+ 0 (* 2
(+ 1 (* 2
(accumulate (lambda (this-coeff higher-terms) <??>)
0
'())))))))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2
(+ 0 (* 2
(+ 1 (* 2 0))))))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2
(+ 0 (* 2
(+ 1 0)))))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2
(+ 0 (* 2 1))))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2
(+ 0 2)))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 (* 2 2))))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2
(+ 5 4)))))))
(+ 1 (* 2
(+ 3 (* 2
(+ 0 (* 2 9))))))
(+ 1 (* 2
(+ 3 (* 2 18))))
(+ 1 (* 2 (+ 3 36)))
(+ 1 (* 2 39))
(+ 1 78)
79
从前面的执行序列的展开部分可以看出, lambda 部分每次的工作就是取出一个因数,
并生成以下表达式(假设当前因数this-coeff为1,x为2):
(+ 1 (* 2 (accumulate ...))),由此可以给出完整的horner-eval函数定义:
;;; 34-horner-eval.scm
(load "p78-accumulate.scm")
(define (horner-eval x coefficient-sequence)
(accumulate (lambda (this-coeff higher-terms)
(+ this-coeff (* x higher-terms)))
0
coefficient-sequence))
测试:
1 ]=> (load "34-horner-eval.scm") ;Loading "34-horner-eval.scm"... ; Loading "p78-accumulate.scm"... done ;... done ;Value: horner-eval 1 ]=> (horner-eval 2 (list 1 3 0 5 0 1)) ;Value: 79
练习 2.35
为2.2.2节的count-leaves重新定义一个累积:
count-leaves函数用于计算一棵树的树叶数量,题目要求我们补充缺少的部分:
(define (count-leaves t)
(accumulate <??> <??> (map <??> <??>)))
根据题目给出的函数形式,猜测有两种可能的办法:
方法一
首先想到的办法可能是,用map函数枚举(enumerate)出所有树叶,然后accumulate
对每个叶子进行+ 1计数,从而计算出整棵树的树叶数量(类似于 练习 2.33 的
length定义)。
使用 练习 2.28 的fringe函数,可以很好地完成枚举出所有树叶的工作:
;;; 28-fringe.scm
(define (fringe tree)
(cond ((null? tree) ; 空树
'())
((not (pair? tree)) ; 叶子
(list tree))
(else
(append (fringe (car tree)) ; 累积左子树所有元素
(fringe (cadr tree)))))) ; 累积右子树所有元素
组合fringe和accumulate(书本 78 页),就可以得出一个计算树叶数量的函数:
;;; 35-count-leaves-using-fringe.scm
(load "28-fringe.scm")
(load "p78-accumulate.scm")
(define (count-leaves tree)
(accumulate (lambda (current-leave remained-leaves-count)
(+ 1 remained-leaves-count))
0
(fringe tree)))
测试count-leaves:
1 ]=> (count-leaves (list (list 1 2) (list 3 4))) ;Value: 4 1 ]=> (count-leaves (list (list 1 (list 2 3)) (list (list 4 5) (list 6 7)))) ;Value: 7
事实上,因为经过fringe处理的树已经是一个普通的(一维)列表了,我们实际上可以
直接通过length函数计算这个列表的长度,从而得出树叶的数量(使用 MIT Scheme
内置的length或者 练习 2.33 实现的length都可以):
;;; 35-count-leaves-using-length.scm
(load "28-fringe.scm")
(define (count-leaves tree)
(length (fringe tree)))
试试这个新的count-leaves:
1 ]=> (load "35-count-leaves-using-length.scm") ;Loading "35-count-leaves-using-length.scm"... ; Loading "28-fringe.scm"... done ;... done ;Value: count-leaves 1 ]=> (count-leaves (list (list 1 2) (list 3 4))) ;Value: 4
方法二
上面定义的count-leaves可以很好地解决计算树叶的问题,但是它不符合题目给定的格式
(只符合了一半):题目要求我们只使用accumulate和map来计算树叶数量,但是
前面的count-leaves定义使用了accumulate和fringe。
定义count-leaves的另一种方法是,map负责计算所有节点的树叶数量,而
accumulate只须将所有节点的树叶数量加起来就行了:(accumulate + 0 ...)。
当map在遍历树的时候,它会遇到两种情况:
-
节点是叶子节点,如果是这样的话,那么返回
1,作为这个节点的树叶数量。 -
节点有左右两个分支,那么这个节点的树叶数量就是这个节点调用
count-leaves函数 的结果。
根据这两条规则,现在可以写出相应的函数了:
;;; 35-count-leaves-using-recursion.scm (load "p78-accumulate.scm") (define (count-leaves tree) (accumulate + 0 (map (lambda (sub-tree) (if (pair? sub-tree) ; 如果这个节点有分支那么这个节点调用 (count-leaves sub-tree) ; count-leaves的结果就是这个节点的树叶数量 1)) ; 遇上一个叶子节点就返回 1 tree)))
测试:
1 ]=> (load "35-count-leaves-using-recursion.scm") ;Loading "35-count-leaves-using-recursion.scm"... ; Loading "p78-accumulate.scm"... done ;... done ;Value: count-leaves 1 ]=> (count-leaves (list (list 1 2) (list 3 4))) ;Value: 4 1 ]=> (count-leaves (list (list 1 (list 2 3)) (list (list 4 5) (list 6 7)))) ;Value: 7
这个count-leaves定义可以很好地完成计算树叶数量的工作,而且只使用了map和
accumulate,符合了题目的要求。
练习 2.36
修改accumulate,创建新的accumulate-n,它最后的参数是一个序列的序列。假设
每个序列的长度一样,过程的作为是累积每个序列的同一个元素,例如:
((1 2 3) (4 5 6) (7 8 9) (10 11 12))
累积为:
(22 26 30)
填充:
(define (accumulate-n op init seqs)
(if (null? (car seqs))
nil
(cons (accumulate op init ??FILL-THIS-IN??)
(accumulate-n op init ??FILL-THIS-IN??))))
假设我们已经有了accumulate-n函数,那么对于表达式
(accumulate-n + 0 (list (list 1 2 3) (list 4 5 6) (list 7 8 9) (list 10 11 12)))
有以下运行序列:
(accumulate-n + 0 (list (list 1 2 3)
(list 4 5 6)
(list 7 8 9)
(list 10 11 12)))
(cons (accumulate + 0 (list 1 4 7 10))
(accumulate-n + 0 (list (list 2 3)
(list 5 6)
(list 8 9)
(list 11 12))))
(cons (accumulate + 0 (list 1 4 7 10))
(cons (accumulate + 0 (list 2 5 8 11))
(accumulate-n + 0 (list (list 3)
(list 6)
(list 9)
(list 12)))))
(cons (accumulate + 0 (list 1 4 7 10))
(cons (accumulate + 0 (list 2 5 8 11))
(cons (accumulate + 0 (list 3 6 9 12))
(accumulate-n + 0 (list '()
'()
'()
'())))))
(cons (accumulate + 0 (list 1 4 7 10))
(cons (accumulate + 0 (list 2 5 8 11))
(cons (accumulate + 0 (list 3 6 9 12))
'())))
(cons 22 (cons 26 (cons 30 '())))
(list 22 26 30)
很明显,解题的关键就是,需要有两个函数:
- 第一个函数取出所有给定列表的第一个元素
- 第二个函数取出所有给定列表除第一个元素之外的其他元素。
car-n
已经知道,函数car可以取出列表的第一个元素,如果要取出多个列表的第一个元素,
可以组合起map和car:
;;; 36-car-n.scm
(define (car-n seqs)
(map car seqs))
测试:
1 ]=> (load "36-car-n.scm")
;Loading "36-car-n.scm"... done
;Value: car-n
1 ]=> (define s (list (list 1 2 3)
(list 4 5 6)
(list 7 8 9)
(list 10 11 12))) ;Value: s
1 ]=> (car-n s) ;Value 11: (1 4 7 10)
cdr-n
另一方面,函数cdr可以用于取出列表除第一个元素之外的其他元素,因此,要取出
多个列表的除第一个元素之外的其他元素,可以组合起map和cdr:
;;; 36-cdr-n.scm
(define (cdr-n seqs)
(map cdr seqs))
测试:
1 ]=> (load "36-cdr-n.scm")
;Loading "36-cdr-n.scm"... done
;Value: cdr-n
1 ]=> (define s (list (list 1 2 3)
(list 4 5 6)
(list 7 8 9)
(list 10 11 12))) ;Value: s
1 ]=> (cdr-n s) ;Value 12: ((2 3) (5 6) (8 9) (11 12))
1 ]=> (cdr-n (cdr-n s)) ;Value 13: ((3) (6) (9) (12))
1 ]=> (cdr-n (cdr-n (cdr-n s))) ;Value 14: (() () () ())
accumulate-n
car-n和cdr-n的运行正如计划之中的一样,现在,组合起题目给出的过程,
给出完整的accumulate-n定义:
;;; 36-accumulate-n.scm
(load "p78-accumulate.scm")
(load "36-car-n.scm")
(load "36-cdr-n.scm")
(define (accumulate-n op init seqs)
(if (null? (car seqs))
'()
(cons (accumulate op init (car-n seqs))
(accumulate-n op init (cdr-n seqs)))))
测试:
1 ]=> (load "36-accumulate-n.scm") ;Loading "36-accumulate-n.scm"... ; Loading "p78-accumulate.scm"... done ; Loading "36-car-n.scm"... done ; Loading "36-cdr-n.scm"... done ;... done ;Value: accumulate-n 1 ]=> (define s (list (list 1 2 3) (list 4 5 6) (list 7 8 9) (list 10 11 12))) ;Value: s 1 ]=> (accumulate-n + 0 s) ;Value 11: (22 26 30)
练习 2.37
把向量\(v = (v_i)\)表示为数的序列,把矩阵\(m=(m_ij)\)表示为向量(矩阵行)的序列, 如:
\[ \begin{equation} \begin{split} \begin{bmatrix} 1 & 2 & 3 & 4 \\ 4 & 5 & 6 & 6 \\ 6 & 7 & 8 & 9 \end{bmatrix} \end{split} \end{equation} \]用以下序列表示:
((1 2 3 4) (4 5 6 6) (6 7 8 9))
目标是为了实现以下矩阵与向量运算:
-
(dot-product v w)返回:和\(\sum_iv_iw_i\) -
(matrix-*-vector m v)返回:向量\(t\),其中\(t_i=\sum_jm_{ij}v_j\) -
(matrix-*-matrix m n)返回:矩阵\(p\),其中\(p_{ij}=\sum_km_{ik}n_{kj}\) -
(transpose m)返回:矩阵\(n\),其中\(n_{ij}=m_{ji}\)
积点定义为:
(define (dot-product v w) (accumulate + 0 (map * v w)))
请完成填空:
(define (matrix-*_vector m v) (map <??> m) (define (transpose mat) (accumulate-n <??> <??> mat)) (define (matrix-*-matrix m n) (let ((cols (transpose n))) (map <??> M)))
matrix-*-vector
矩阵m和向量v之间的乘法可以这样来完成:
取出矩阵m中的各列col,并计算col和向量v之间的点积。
取出矩阵各列的操作可以使用map函数来完成:
(map (lambda (col)
...)
m)
而矩阵的各个列(它们也是向量)和给定向量v之间的点积可以通过dot-product进行:
(dot-product col v)
组合起以上两个操作,就得出了matrix-*-vector的定义:
;;; 37-matrix-*-vector.scm
(load "37-dot-product.scm")
(define (matrix-*-vector m v)
(map (lambda (col)
(dot-product col v))
m))
测试:
1 ]=> (load "37-matrix-*-vector.scm")
;Loading "37-matrix-*-vector.scm"...
;Warning: Ill-formed file attributes line.
; Loading "37-dot-product.scm"...
; Loading "p78-accumulate.scm"... done
; ... done
;... done
;Value: matrix-*-vector
1 ]=> (define m (list (list 1 2 3 4)
(list 4 5 6 6)
(list 6 7 8 9))) ;Value: m
1 ]=> (define v (list 1 2 3 4)) ;Value: v
1 ]=> (matrix-*-vector m v) ;Value 23: (30 56 80)
transpose
transpose函数先取出矩阵内所有列表的car部分,将它们组成一个新的列表,
作为新矩阵的第一列;接着取出矩阵内所有列表的cadr部分,将它们组成一个新的列表
,作为新矩阵的第二列,以此类推,一直到整个矩阵处理完为止:
;;; 37-transpose.scm
(load "36-accumulate-n.scm")
(define (transpose m)
(accumulate-n cons '() m))
测试:
1 ]=> (load "37-transpose.scm")
;Loading "37-transpose.scm"...
; Loading "36-accumulate-n.scm"...
; Loading "p78-accumulate.scm"... done
; Loading "36-car-n.scm"... done
; Loading "36-cdr-n.scm"... done
; ... done
;... done
;Value: transpose
1 ]=> (define m (list (list 1 2 3 4)
(list 4 5 6 6)
(list 6 7 8 9))) ;Value: m
1 ]=> (transpose m) ;Value 11: ((1 4 6) (2 5 7) (3 6 8) (4 6 9))
以下是(transpose m)执行时产生的调用序列:
(transpose (list (list 1 2 3 4)
(list 4 5 6 6)
(list 6 7 8 9)))
(cons (accumulate cons '() (list 1 4 6))
(accumulate-n cons '() (list (list 2 3 4)
(list 5 6 6)
(list 7 8 9))))
(cons (accumulate cons '() (list 1 4 6))
(cons (accumulate cons '() (list 2 5 7))
(accumulate-n cons '() (list (list 3 4)
(list 6 6)
(list 8 9)))))
(cons (accumulate cons '() (list 1 4 6))
(cons (accumulate cons '() (list 2 5 7))
(cons (accumulate cons '() (list 3 6 8))
(accumulate-n cons '() (list (list 4)
(list 6)
(list 9))))))
(cons (accumulate cons '() (list 1 4 6))
(cons (accumulate cons '() (list 2 5 7))
(cons (accumulate cons '() (list 3 6 8))
(cons (accumulate cons '() (list 4 6 9))
(accumulate-n cons '() (list '() '() '()))))))
(cons (list 1 4 6)
(cons (list 2 5 7)
(cons (list 3 6 8)
(cons (list 4 6 9)
'()))))
(list (list 1 4 6)
(list 2 5 7)
(list 3 6 8)
(list 4 6 9))
matrix-*-matrix
矩阵和矩阵之间的乘法规则:对于两个矩阵m和n,当m * n时,mn的第一列
第一行的值为m的第一列和n的第一行的点积,mn的第一列第二行的值为m的第一列
和n的第二行的点积,以此类推。
比如说,当m为以下矩阵:
(list (list 1 2 3 4)
(list 4 5 6 6)
(list 6 7 8 9))
而n为以下矩阵(m的transpose):
(list (list 1 4 6)
(list 2 5 7)
(list 3 6 8)
(list 4 6 9))
那么mn的第一列的值可以通过以下方法计算得出:
(let ((col-of-m (car m)))
(list (dot-product col-of-m
(car-n n)))
(dot-product col-of-m
(car-n (cdr-n n)))
(dot-product col-of-m
(car-n (cdr-n (cdr-n n)))))
将以上的方法进行推广,就得出了矩阵乘法函数的定义:
;;; 37-matrix-*-matrix.scm
(load "37-transpose.scm")
(load "37-dot-product.scm")
(define (matrix-*-matrix m n)
(let ((cols (transpose n)))
(map (lambda (col-of-m)
(map (lambda (col-of-cols)
(dot-product col-of-m
col-of-cols))
cols))
m)))
matrix-*-matrix的定义中没有用到car-n和cdr-n,取出矩阵n各个行的工作由
transpose和map完成:
先使用transpose将n翻转,然后使用map对转换后的矩阵的列进行遍历,就可以
取出矩阵n的各个行了。
测试:
1 ]=> (load "37-matrix-*-matrix.scm")
;Loading "37-matrix-*-matrix.scm"...
;Warning: Ill-formed file attributes line.
; Loading "37-transpose.scm"...
; Loading "36-accumulate-n.scm"...
; Loading "p78-accumulate.scm"... done
; Loading "36-car-n.scm"... done
; Loading "36-cdr-n.scm"... done
; ... done
; ... done
; Loading "37-dot-product.scm"...
; Loading "p78-accumulate.scm"... done
; ... done
;... done
;Value: matrix-*-matrix
1 ]=> (load "37-transpose.scm")
;Loading "37-transpose.scm"...
; Loading "36-accumulate-n.scm"...
; Loading "p78-accumulate.scm"... done
; Loading "36-car-n.scm"... done
; Loading "36-cdr-n.scm"... done
; ... done
;... done
;Value: transpose
1 ]=> (define m (list (list 1 2 3 4)
(list 4 5 6 6)
(list 6 7 8 9))) ;Value: m
1 ]=> (matrix-*-matrix m (transpose m))
;Value 19: ((30 56 80) (56 113 161) (80 161 230))
定义matrix-*-matrix的另一种方式是不直接用map处理m和n的各个向量,
而是使用matrix-*-vector函数,让矩阵(transpose n)去乘m的各个col:
;;; 37-matrix-*-matrix-another.scm
(load "37-transpose.scm")
(load "37-matrix-*-vector.scm")
(define (matrix-*-matrix m n)
(let ((trans-n (transpose n)))
(map (lambda (col-of-m)
(matrix-*-vector trans-n col-of-m))
m)))
这个解法本质上和第一种解法是一样的,只是这个解法相对更高阶一些。
练习 2.38
accumulate过程其实就是flod-right的实现,对应的有flood-left:
(define (fold-left op initial sequence)
(define (iter result rest)
(if (null? rest)
result
(iter (op result (car rest))
(cdr rest))))
(iter initial sequence))
求以下表达式的值:
(fold-right / 1 (list 1 2 3)) (fold-left / 1 (list 1 2 3)) (fold-right list nil (list 1 2 3)) (fold-left list nil (list 1 2 3))
op要有怎么样的特性,可以让fold-right和fold-left的结果相同?
fold-left 直接对着题目敲下来就行了。而 fold-right 也只是简单地对书本 78 页的
accumulate函数进行改名:
;;; p78-accumulate.scm
(define (accumulate op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(accumulate op initial (cdr sequence)))))
(define fold-right accumulate)
求值
表达式(fold-right / 1 (list 1 2 3))的计算序列是:
(/ 1 (/ 2 (/ 3 1))) (/ 1 (/ 2 3)) (/ 1 2/3) 3/2
表达式(fold-left / (list 1 2 3))的计算序列是:
(/ (/ (/ 1 1) 2) 3) (/ (/ (/ 1 1) 2) 3) (/ (/ 1 2) 3) (/ 1/2 3) 1/6
表达式(fold-right list '() (list 1 2 3))的计算序列是:
(list 1 (list 2 (list 3 '()))) (list 1 (list 2 (3 '()))) (list 1 (2 (3 '()))) (1 (2 (3 '())))
注意,()是求值器对'()的打印格式,展开代码中使用了'()而不是(),
注意不要把它们搞混了。
表达式(fold-left list '() (list 1 2 3))的计算序列是:
(list (list (list '() 1) 2) 3)
(list (list ('() 1) 2) 3)
(list (('() 1) 2) 3)
((('() 1) 2) 3)
fold-left 和 fold-right 产生同样的结果
因为fold-left和fold-right生成的计算序列不同,要让它们的计算产生同样的结果,
一个办法就是要求op参数,也即是传入的操作函数必须符合结合律(monoid)。
比如说,\和list函数都不符合结合律,
另一方面,像+、*、or和and那样的函数,就是符合结合律的函数。
让fold-left和fold-right得出同样结果的另一种办法是,在fold-left和
fold-right之间进行转换,从而让两个函数产生同样的计算序列,练习2.39就是
这样的一个例子。
See also
- 维基百科的 Fold 词条 给出了关于 fold 的主要特性。link
- 论文 A tutorial on the universality and expressiveness of fold 给出了很多 fold 操作的例子,非常实用。link
- 书本 《Introduction to Functional Programming》(第一版) 在 3.5 节讲到了结合律在函数中的应用。link
练习 2.39
用让fold-left和fold-right完成reverse(练习2.18)的定义:
(define (reverse sequence) (fold-right (lambda (x y) <??> nil sequence)) (define (reverse sequence) (fold-left (lambda (x y) <??> nil sequence))
fold-left的展开规则为(使用列表(list 1 2 3 4)作为例子):
(fold-left f '() (list 1 2 3 4)) (... (f '() 1) ...) (... (f (f '() 1) 2) ...) (... (f (f (f '() 1) 2) 3) ...) (f (f (f (f '() 1) 2) 3) 4)
而要生成列表的逆序,我们需要这样一个计算序列:
(reverse (list 1 2 3 4)) (... (cons 1 '()) ...) (... (cons 2 (cons 1 '())) ...) (... (cons 3 (cons 2 (cons 1 '()))) ...) (cons 4 (cons 3 (cons 2 (cons 1 '()))))
可以看出,这两个计算序列非常相似,唯一的不同就是函数f和函数cons的参数位置
不同,不过这个问题并不难解决,只要在函数体内调整两个参数的位置就行了:
(lambda (x y) (cons y x))
综合上面叙述,可以给出相应的函数:
;;; 39-reverse-using-fold-left.scm
(define (reverse sequence)
(fold-left (lambda (x y)
(cons y x))
'()
sequence))
测试:
1 ]=> (load "39-reverse-using-fold-left.scm") ;Loading "39-reverse-using-fold-left.scm"... done ;Value: reverse 1 ]=> (reverse (list 1 2 3 4)) ;Value 11: (4 3 2 1)
测试所执行的表达式的展开过程和前面给出的展开过程完全一样。
fold-right
先分析fold-right的展开序列:
(fold-right f '() (list 1 2 3 4)) (f 1 ...) (f 1 (f 2 ...)) (f 1 (f 2 (f 3 ...))) (f 1 (f 2 (f 3 (f 4 ...)))) (f 1 (f 2 (f 3 (f 4 '()))))
要生成列表的逆序,我们需要让fold-right生成这样一个计算序列:
(reverse (list 1 2 3 4)) (fold-right g '() (list 1 2 3 4)) (... (g 4 '()) ...) (... (g (g 4 '()) 3) ...) (... (g (g (g 4 '()) 3) 2) ...) (g (g (g (g 4 '()) 3) 2) 1)
要倒转函数的组合顺序,可以通过在函数体内调整参数的位置来做到这一点:
(lambda (x y) (g y x))
问题的关键就是找出函数g,从fold-left的经验看来,cons很有可能就是g,而且
(cons 4 '())似乎也说得过去,不过当计算进展到第二步时,计算就变成了
(cons (cons 4 '()) 3),这时再用cons就说不通了,因此cons不是我们所寻找的
函数g。
从cons失败的经验来看,g应该不仅仅能处理单个元素,它还应该能将一个列表和
单个元素组合起来形成一个新列表,这也就是书本68页介绍过的append函数:
1 ]=> (append (list 1 2 3) (list 4 5 6)) ;Value 12: (1 2 3 4 5 6)
虽然append要求两个参数都是列表,但是让一个列表和单个元素组合起来也不太难,
只要将单个元素转换成一个包含单个元素的列表就行了:
1 ]=> (append (list 1 2 3) 4) ; 组合单个元素
;Value 13: (1 2 3 . 4)
1 ]=> (append (list 1 2 3) (list 4)) ; 组合两个列表
;Value 14: (1 2 3 4)
这样的话,函数g的定义终于浮出水面了:
(lambda (x y) (append y (list x)))
根据以上给出的条件,现在可以写出用fold-right实现的reverse函数了:
;;; 39-reverse-using-fold-right.scm
(define (reverse sequence)
(fold-right (lambda (x y)
(append y (list x)))
'()
sequence))
测试:
1 ]=> (load "39-reverse-using-fold-right.scm") ;Loading "39-reverse-using-fold-right.scm"... done ;Value: reverse 1 ]=> (reverse (list 1 2 3 4 5 6 7)) ;Value 12: (7 6 5 4 3 2 1)
这个表达式的计算展开是:
(reverse (list 1 2 3 4 5 6 7)) (append '() (list 7)) (append '(7) (list 6)) (append '(7 6) (list 5)) (append '(7 6 5) (list 4)) (append '(7 6 5 4) (list 3)) (append '(7 6 5 4 3) (list 2)) (append '(7 6 5 4 3 2) (list 1)) '(7 6 5 4 3 2 1)
效率
我们分别使用fold-left和fold-right两种方法定义了reverse函数,除了
实现方面的不同外,它们的效率也有很大的区别:
fold-left实现的reverse每次都递归地使用cons组合起一个元素和一个列表,
每次组合操作的时间复杂度为\(O(1)\),空间复杂度为\(O(1)\),翻转整个列表所需的
时间复杂度为\(O(n)\),空间的复杂度也为\(O(n)\),它是一个线性复杂度的线性递归过程。
另一方面,fold-right实现的reverse每次都递归地使用append将一个列表和
一个包含单个元素的列表组合起来,每次组合操作的时间复杂度为\(O(n)\),
空间复杂度为\(O(1)\),翻转整个列表所需的时间复杂度为\(O(n^2)\),而空间复杂度为
$\(O(n)4\),它是一个二次复杂度的线性递归过程。
实例:一个图形语言
图形语言
画家(painter)决定画的图像。比如画家wave画出简笔画,而画家rogers画出人像。

框架决定画像的大小与形状:

基本的操作过程:
-
flip-vert过程上下反转画家。 -
flip-horiz过程上下反转画家。 -
beside过程并排两个画家。 -
below过程上下排两个画家。
应用闭包性质,复合操作:
(define wave2 (beside wave (flip-vert wave)))
(define wave4 (below wave2 wave2))
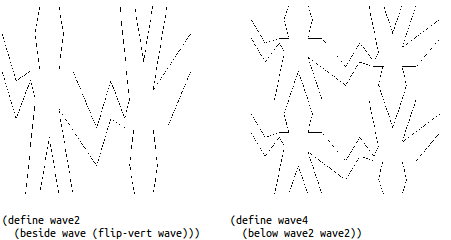
以上的程序只能应用在wave这一个画家上,进一步抽象出组合的逻辑,以任意一个画家
作为参数实现四个组合:
(define (flipped-pairs painter) (let ((painter2 (beside painter (flip-vert painter)))) (below painter2 painter2)))
如果把wave作为参数:
(define wave4 (flipped-pairs wave))
在图形上做出递归的分支:
(define (right-split painter n)
(if (= n 0)
painter
(let ((smaller (right-split painter (- n 1))))
(beside painter (below smaller smaller)))))
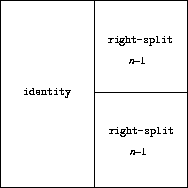
(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1))))
(let ((top-left (beside up up))
(bottom-right (below right right))
(corner (corner-split painter (- n 1))))
(beside (below painter top-left)
(below bottom-right corner))))))
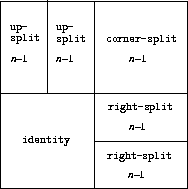
应用不同组合的效果:

把四个corner-split组合,可以得到square-limit的模式:
(define (square-limit painter n) (let ((quarter (corner-split painter n))) (let ((half (beside (flip-horiz quarter) quarter))) (below (flip-vert half) half))))

练习 2.44
定义出corner-split里使用的过程up-split,它与right-split类似,除在其中交换
了below和beside的角色之个。
up-split的定义和right-split的定义非常相似,唯一的区别是beside和below的
位置不同:
;;; 44-up-split.scm
(define (up-split painter n)
(if (= n 0)
painter
(let ((smaller (up-split painter (- n 1))))
(below painter
(beside smaller smaller)))))
高阶操作
把画家作为参数,实现可利用的过程。
以下的过程生成「田」字形拼在一起的四张图片。但每个图片的旋转角度作为参数:
(define (square-of-four tl tr bl br)
(lambda (painter)
(let ((top (beside (tl painter) (tr painter)))
(bottom (beside (bl painter) (br painter))))
(below bottom top))))
通过不同的参数指定四个图片的方向:
(define (flipped-pairs painter)
(let ((combine4 (square-of-four identity flip-vert
identity flip-vert)))
(combine4 painter)))
以上的过程可以简写为:
(define flipped-pairs (square-of-four identity flip-vert identity flip-vert))
另一种组合:
(define (square-limit painter n)
(let ((combine4 (square-of-four flip-horiz identity
rotate180 flip-vert)))
(combine4 (corner-split painter n))))
其中的rotate180是练习2.50中的过程。不用rotate180也可以用练习1.42的compose
过程:
(compose flip-vert flip-horiz)
练习 2.45
right-split和up-split可以抽象出共同的逻辑split,它满足:
(define right-split (split beside below)) (define up-split (split below beside))
从 up-split 和 right-split 中抽取出一个通用的 split 抽象:
;;; 45-split.scm
(define (split big-combiner small-combiner)
(lambda (painter n)
(if (= n 0)
painter
(let ((smaller
((split big-combiner small-combiner) painter (- n 1))))
(big-combiner painter
(small-combiner smaller smaller))))))
前面的 split 函数,因为缺少一种引用自身的手段,所以 let 部分的代码非常长,一种缩短代码的办法是使用一个辅助函数:
;;; 45-another.scm
(define (split big-combiner small-combiner)
(define (inner painter n)
(if (= n 0)
painter
(let ((smaller (inner painter (- n 1))))
(big-combiner painter
(small-combiner smaller smaller)))))
inner)
新的 split 避免了过长的 let 表达式,但仍然有一个不太美观的地方:它在最后需要返回 inner 函数。
使用 split 重定义 up-split
;;; 45-up-split.scm (load "45-split.scm") (define up-split (split below beside))
使用 split 重定义 up-split
;;; 45-right-split.scm (load "45-split.scm") (define right-split (split beside below))
框架
框架可以用三个向量来描述:
- 一个基准向量:框架基准点与原点的偏移量。
-
两个角向量:框架的角对于框架基准点的偏量。
- 如果两个角向量正交,框架是矩形。
- 如果两个角向量非正交,框架是平行四边形。
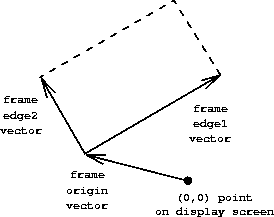
代码描述:
-
构造函数:
make-frame -
选择函数:
origin-frame -
选择函数:
edge1-frame -
选择函数:
edge2-frame
在这里用单位正方形\((0 \leq x, y \leq 1)\)描述坐标。每个框架要关联坐标映射来完成 图像的位移和伸缩:
\[ \begin{equation} \begin{split} Origin(Frame) + x \cdot Edge_1(Frame) + y \cdot Edge_2(Frame) \end{split} \end{equation} \]
例:点\((0,0)\)被映射到框架原点,\((1,1)\)被映射到与原点对角的那个点,\((0.5, 0.5)\)
被映射到给定框架的中心点。框架的坐标映射就如frame-coord-map所示,以框架作为
参数返回值是一个过程:
(define (frame-coord-map frame)
(lambda (v)
(add-vect
(origin-frame frame)
(add-vect (scale-vect (xcor-vect v)
(edge1-frame frame))
(scale-vect (ycor-vect v)
(edge2-frame frame))))))
返回的过程以向量v作为参数,返回另一个向量。如果参数向量位于单位正方形里,结果
向量也在相应的框架里,如:
((frame-coord-map a-frame) (make-vect 0 0))
返回的向量为:
(origin-frame a-frame)
练习 2.46 向量的定义与运算
实现从原点出发的二维向量用\((x, y)\),包括:
-
构造函数:
make-vect -
选择函数:
xcor-vect、ycor-vect -
加法运算:
add-vect、减法运算:sub-vect、缩放运算:scale--vect
向量的表示
定义:
;;; 46-vect-represent.scm (define (make-vect xcor ycor) (list xcor ycor)) (define (xcor-vect v) (car v)) (define (ycor-vect v) (cadr v))
测试:
(load "46-vect-represent.scm") (define v (make-vect 0.5 1)) ;Value: v (xcor-vect v) ;Value: .5 (ycor-vect v) ;Value: 1
add-vect
;;; 46-add-vect.scm
(load "46-vect-represent.scm")
(define (add-vect vect another-vect)
(make-vect (+ (xcor-vect vect)
(xcor-vect another-vect))
(+ (ycor-vect vect)
(ycor-vect another-vect))))
测试:
1 ]=> (load "46-add-vect.scm")
1 ]=> (define sum (add-vect (make-vect 0.5 0.5)
(make-vect 0.2 0.2)))
1 ]=> (xcor-vect sum) ;Value: .7
1 ]=> (ycor-vect sum) ;Value: .7
sub-vect
;;; 46-sub-vect.scm
(load "46-vect-represent.scm")
(define (sub-vect vect another-vect)
(make-vect (- (xcor-vect vect)
(xcor-vect another-vect))
(- (ycor-vect vect)
(ycor-vect another-vect))))
测试:
1 ]=> (load "46-sub-vect.scm")
1 ]=> (define diff (sub-vect (make-vect 0.5 0.5)
(make-vect 0.2 0.2)))
1 ]=> (xcor-vect diff) ;Value: .3
1 ]=> (ycor-vect diff) ;Value: .3
scale-vect
;;; 46-scale-vect.scm
(load "46-vect-represent.scm")
(define (scale-vect factor vect)
(make-vect (* factor (xcor-vect vect))
(* factor (ycor-vect vect))))
测试:
1 ]=> (load "46-scale-vect.scm") 1 ]=> (define product (scale-vect 2 (make-vect 0.3 0.3))) 1 ]=> (xcor-vect product) ;Value: .6 1 ]=> (ycor-vect product) ;Value: .6
练习 2.47 框架的实现
实现框架的两个可能的过程函数:
(define (make-frame origin edge1 edge2) (list origin edge1 edge2)) (define (make-frame origin edge1 edge2) (cons origin (cons edge1 edge2)))
请定义出适当的选择函数。
实现一
定义:
;;; 47-frame-represent-using-list.scm (define (make-frame origin edge1 edge2) (list origin edge1 edge2)) (define (origin-frame f) (car f)) (define (edge1-frame f) (cadr f)) (define (edge2-frame f) (caddr f))
测试:
(load "47-frame-represent-using-list.scm")
(load "46-vect-represent.scm") ; 还需要练习 46 的向量表示
(define f (make-frame (make-vect 0.0 0.0) ; origin
(make-vect 0.3 0.3) ; edge1
(make-vect 0.6 0.6))) ; edge2
(origin-frame f) ;Value 11: (0. 0.)
(edge1-frame f) ;Value 12: (.3 .3)
(edge2-frame f) ;Value 13: (.6 .6)
实现二
定义:
;;; 47-frame-represent-using-cons.scm
(define (make-frame origin edge1 edge2)
(cons origin
(cons edge1 edge2)))
(define (origin-frame f) (car f))
(define (edge1-frame f) (cadr f))
(define (edge2-frame f) (cddr f))
测试:
(load "47-frame-represent-using-cons.scm")
(load "46-vect-represent.scm") ; 还需要练习 46 的向量表示
(define f (make-frame (make-vect 0.0 0.0) ; origin
(make-vect 0.3 0.3) ; edge1
(make-vect 0.6 0.6))) ; edge2
(origin-frame f) ;Value 11: (0. 0.)
(edge1-frame f) ;Value 12: (.3 .3)
(edge2-frame f) ;Value 13: (.6 .6)
画家
画家被表示为一个过程,以一个框架为参数,就可以按框架的位移的变形生成图像。 这样的抽象屏障把图像的内容(画家)与显示的方式(框架)解耦。
例:draw-line以两点为参数画直线,通过它可以实现wave(还要用到练习 2.48里的
线段描述,和练习 2.23里的for-each过程):
(define (segments->painter segment-list)
(lambda (frame) ;; 返回值是过程
(for-each
(lambda (segment) ;; 定义lambda
(draw-line
((frame-coord-map frame) (start-segment segment))
((frame-coord-map frame) (end-segment segment))))
segment-list))) ;; for-each segment-list中每一个值
练习 2.48 用向量表示线段
线段可以由两个向量表示:
- 原点到起点的向量
- 起点到终点的向量
实现这个想法,定义结构函数make-segment和选择函数start-segment、
end-segment。
其实在 练习 2.2 我们已经做过类似的练习了,做法是一样的:
;;; 48-segment-represent.scm (define (make-segment start end) (list start end)) (define (start-segment s) (car s)) (define (end-segment s) (cadr s))
测试:
(load "48-segment-represent.scm")
(load "46-vect-represent.scm")
(define seg (make-segment (make-vect 0.0 0.0)
(make-vect 1.0 1.0)))
(start-segment seg) ;Value 11: (0. 0.)
(end-segment seg) ;Value 12: (1. 1.)
练习 2.49 实现各种画家
利用segments->painter来实现各种画家。
See also
一个网上的 app 可以很方便地对画家进行测试: http://www.biwascheme.org/repos/demo/pictlang.html , 语法和题目用的稍微有一点不同,但是不难学会。
以下将在每个画家的例子的最后附上该 app 的测试代码,可以用这些测试代码在 app 上实验画图。
a) 可以画出框架的边界的画家
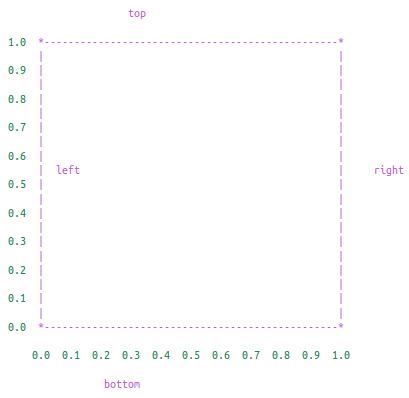
画出框架边界需要四条线段,分别是:
(define top-left (make-vect 0.0 1.0)) (define top-right (make-vect 1.0 1.0)) (define bottom-left (make-vect 0.0 0.0)) (define bottom-right (make-vect 1.0 0.0)) (define top (make-segment top-left top-right)) (define left (make-segment top-left bottom-left)) (define right (make-segment top-right bottom-right)) (define bottom (make-segment bottom-left bottom-right))
执行以下表达式可以生成画出给定框架边界的画家:
(segments->painter (list top bottom left right))
See also 测试代码:
(define top-left (make-vect 0.0 1.0)) (define top-right (make-vect 1.0 1.0)) (define bottom-left (make-vect 0.0 0.0)) (define bottom-right (make-vect 1.0 0.0)) ($line top-left top-right) ($line top-left bottom-left) ($line top-right bottom-right) ($line bottom-left bottom-right)
b) 连接对角画个叉
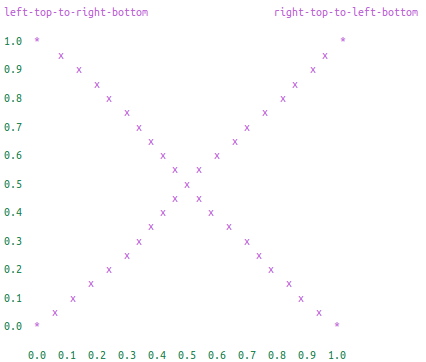
画出这样的叉子需要两条线段,分别在左上至右下和右上至左下各一条:
(define left-top (make-vect 0.0 1.0))
(define right-bottom (make-vect 1.0 0.0))
(define right-top (make-vect 1.0 1.0))
(define left-bottom (make-vect 0.0 0.0))
(define left-top-to-right-bottom (make-segment left-top
right-bottom))
(define right-top-to-left-bottom (make-segment right-top
left-bottom))
执行以下表达式将生成一个划出对角大叉子的画家:
(segments->painter (list left-top-to-right-bottom
right-top-to-left-bottom))
See also 测试代码:
(define left-top (make-vect 0.0 1.0)) (define right-bottom (make-vect 1.0 0.0)) (define right-top (make-vect 1.0 1.0)) (define left-bottom (make-vect 0.0 0.0)) ($line left-top right-bottom) ($line right-top left-bottom)
c) 连接边的中点画个菱形
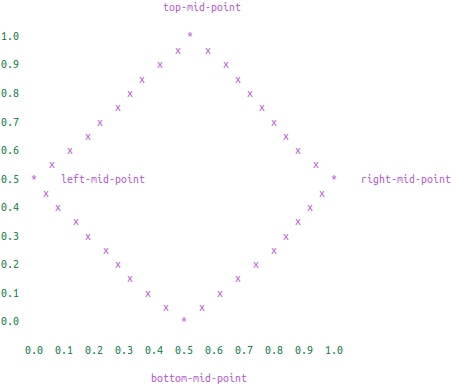
划出这样的菱形需要四条边,分别连接到四个中点:
(define top-mid-point (make-vect 0.5 1.0))
(define bottom-mid-point (make-vect 0.5 0.0))
(define left-mid-point (make-vect 0.0 0.5))
(define right-mid-point (make-vect 1.0 0.5))
(define top-to-left (make-segment top-mid-point
left-mid-point))
(define top-to-right (make-segment top-mid-point
right-mid-point))
(define bottom-to-left (make-segment bottom-mid-point
left-mid-point))
(define bottom-to-right (make-segment bottom-mid-point
right-mid-point))
执行以下表达式将创建一个划出菱形的画家:
(segments->painter (list top-to-left
top-to-right
bottom-to-left
bottom-to-right))
See also 测试代码:
(define top-mid-point (make-vect 0.5 1.0)) (define bottom-mid-point (make-vect 0.5 0.0)) (define left-mid-point (make-vect 0.0 0.5)) (define right-mid-point (make-vect 1.0 0.5)) ; top to left ($line top-mid-point left-mid-point) ; top to right ($line top-mid-point right-mid-point) ; bottom to left ($line bottom-mid-point left-mid-point) ; bottom to right ($line bottom-mid-point right-mid-point)
d) 实现wave
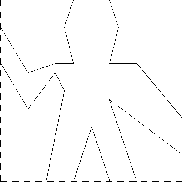
wave 的图形比前面的复杂很多,而且没有准确的坐标点可以参考: 以下是生成画出 wave 画家的线段,使用的坐标是大致测量得出的(共 17 条线段):
(segments->painter (list
(make-segment (make-vect 0.4 1.0) ; 头部左上
(make-vect 0.35 0.85))
(make-segment (make-vect 0.35 0.85) ; 头部左下
(make-vect 0.4 0.64))
(make-segment (make-vect 0.4 0.65) ; 左肩
(make-vect 0.25 0.65))
(make-segment (make-vect 0.25 0.65) ; 左手臂上部
(make-vect 0.15 0.6))
(make-segment (make-vect 0.15 0.6) ; 左手上部
(make-vect 0.0 0.85))
(make-segment (make-vect 0.0 0.65) ; 左手下部
(make-vect 0.15 0.35))
(make-segment (make-vect 0.15 0.35) ; 左手臂下部
(make-vect 0.25 0.6))
(make-segment (make-vect 0.25 0.6) ; 左边身体
(make-vect 0.35 0.5))
(make-segment (make-vect 0.35 0.5) ; 左腿外侧
(make-vect 0.25 0.0))
(make-segment (make-vect 0.6 1.0) ; 头部右上
(make-vect 0.65 0.85))
(make-segment (make-vect 0.65 0.85) ; 头部右下
(make-vect 0.6 0.65))
(make-segment (make-vect 0.6 0.65) ; 右肩
(make-vect 0.75 0.65))
(make-segment (make-vect 0.75 0.65) ; 右手上部
(make-vect 1.0 0.3))
(make-segment (make-vect 1.0 0.15) ; 右手下部
(make-vect 0.6 0.5))
(make-segment (make-vect 0.6 0.5) ; 右腿外侧
(make-vect 0.75 0.0))
(make-segment (make-vect 0.4 0.0) ; 左腿内侧
(make-vect 0.5 0.3))
(make-segment (make-vect 0.6 0.0) ; 右腿内侧
(make-vect 0.5 0.3))))
See also 测试代码:
; 左上部 ($line (make-vect 0.4 1.0) (make-vect 0.35 0.85) (make-vect 0.4 0.65) (make-vect 0.25 0.65) (make-vect 0.15 0.6) (make-vect 0.0 0.85)) ; 右上部 ($line (make-vect 0.6 1.0) (make-vect 0.65 0.85) (make-vect 0.6 0.65) (make-vect 0.75 0.65) (make-vect 1.0 0.3)) ; 左下部 ($line (make-vect 0.0 0.65) (make-vect 0.15 0.35) (make-vect 0.25 0.6) (make-vect 0.35 0.5) (make-vect 0.25 0.0)) ; 右下部 ($line (make-vect 1.0 0.15) (make-vect 0.6 0.5) (make-vect 0.75 0.0)) ; 内侧 ($line (make-vect 0.6 0.0) (make-vect 0.5 0.3) (make-vect 0.4 0.0))
画家的变换和组合
同样的画家,只要换一个框架就可以生成新的图像,比如flip-vert翻转图像。
这一类操作抽象为transform-painter,参数包括一个画家和如何变换的信息。
实际完成的是对框架的一次变换,并用生成的框架去调用原来的画家。
方法的参数包括:
- 一个画家
- 新框架的原点
- 新框架的两个边向量的终点
(define (transform-painter painter origin corner1 corner2)
(lambda (frame)
(let ((m (frame-coord-map frame)))
(let ((new-origin (m origin)))
(painter
(make-frame new-origin
(sub-vect (m corner1) new-origin)
(sub-vect (m corner2) new-origin)))))))
反转画家的定义:
(define (flip-vert painter)
(transform-painter painter
(make-vect 0.0 1.0) ; new origin
(make-vect 1.0 1.0) ; new end of edge1
(make-vect 0.0 0.0))) ; new end of edge2
缩小到右上的四分之一:
(define (shrink-to-upper-right painter)
(transform-painter painter
(make-vect 0.5 0.5)
(make-vect 1.0 0.5)
(make-vect 0.5 1.0)))
逆时针转90度:
(define (rotate90 painter)
(transform-painter painter
(make-vect 1.0 0.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0)))
收缩到中心:
(define (squash-inwards painter)
(transform-painter painter
(make-vect 0.0 0.0)
(make-vect 0.65 0.35)
(make-vect 0.35 0.65)))
还可以组合多个画家,如beside以两个画家为参数,缩小到左右两边,在这个过程中完全
不需要知道与画家相关的信息,只要知道框架的变换就可以了:
(define (beside painter1 painter2)
(let ((split-point (make-vect 0.5 0.0)))
(let ((paint-left
(transform-painter painter1
(make-vect 0.0 0.0)
split-point
(make-vect 0.0 1.0)))
(paint-right
(transform-painter painter2
split-point
(make-vect 1.0 0.0)
(make-vect 0.5 1.0))))
(lambda (frame)
(paint-left frame)
(paint-right frame)))))
练习 2.50
使用书本 94 页提供的 flip-vert 函数,可以将通过翻转框架来画出一个水平翻转:
;;; p94-flip-vert.scm
(define (flip-vect painter)
(transform-painter painter
(make-vect 0.0 1.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0)))
使用书本 94 页提供的 rotate90 函数,可以将框架逆时针旋转 90 度:
;;; p94-rotate90.scm
(define (rotate90 painter)
(transform-painter painter
(make-vect 1.0 0.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0)))
水平翻转是 flip-horiz 的定义:
;;; 50-flip-horiz.scm
(define (flip-horiz painter)
(transform-painter painter
(make-vect 1.0 0.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0)))
180度rotate180:
;;; 50-rotate180.scm
(define (rotate180 painter)
(transform-painter painter
(make-vect 1.0 1.0)
(make-vect 0.0 1.0)
(make-vect 1.0 0.0)))
使用 rotate270 对画家进行逆时针 270 度翻转的过程:
;;; 50-rotate270.scm
(define (rotate270 painter)
(transform-painter painter
(make-vect 0.0 1.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0)))
练习 2.51
定义below把两个画家放在上下两部分。要求用两个方法实现:
- 直接上下接
- 用beside左右接,然后旋转
直接拼接:
;;; 51-below.scm
(define (below painter1 painter2)
(let ((split-point (make-vect 0.0 0.5)))
(let ((paint-top
(transform-painter painter2
split-point
(make-vect 1.0 0.5)
(make-vect 0.0 1.0)))
(paint-down
(transform-painter painter1
(make-vect 0.0 0.0)
(make-vect 1.0 0.0)
split-point)))
(lambda (frame)
(paint-top frame)
(paint-down frame)))))
左右接然后旋转:
以下是只使用 beside 和旋转来完成 below 过程的步骤:
- 分别对 painter1 和 painter2 调用 flip-horiz ,产生新的 painter1 和 painter2
- 分别对新的 painter1 和 painter2 调用 rotate270 ,产生新的 painter1 和 painter2
- 使用 beside ,将新的 painter1 和 painter2 组合起来,产生 beside-painter
- 对 beside-painter 调用 rotate90 ,产生新的 beside-painter
- 对新的 beside-painter 调用 flip-horiz ,得出和 below 一样的效果
前面的这五个步骤实际上是一个回溯得出的计算结果,从最后一步往前看,会更容易弄清楚这个 below 的效果是如何实现的。
另外,在对图形进行翻转的时候,我们假设图片是自伸缩的,也即是,它可以自动地根据 框架的大小来进行放大和缩小。在一个实际的图形处理语言中,进行翻转的时候,还必须 进行缩放,确保图片能正确地显示在给定的框架内。
这个 below 的定义如下:
;;; 51-another-below.scm
(define (below painter1 painter2)
(lambda (frame)
((flip-horiz
(rotate90
(beside
(rotate270
(flip-horiz painter1))
(rotate270
(flip-horiz painter2)))))
frame)))
强健设计的语言层次
- 用过程实现数据结构,可以用统一方式处理不同的问题。
- 用满足闭包的方式组合,可以构造各种复杂的设计。
- 分层,每一层解决不同的问题,且不用关心其他层如何实现。
练习 2.52
对下图进行改进:

a) 给wave加上线条,比如笑脸:
要给 wave 图形加上线段,直接在调用 segments->painter 的时候添加就可以了。
以下代码将给 wave 图形加上一条对角线:
(segments->painter (list (make-segment (make-vect 0.0 0.0)
(make-vect 1.0 1.0))
; ... wave 图形的线段
))
b) 修改corner-split的构造模式,如只用up-split和right-split的一个副本,
而不是两个:
以下是只使用一个 up-split 图像和只使用一个 right-split 图像定义的 corner-split (当然,这个定义和原本的定义产生的图像有一点不同):
;;; 52-corner-split.scm
(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1)))
(corner (corner-split painter (- n 1))))
(beside (below painter up)
(below right corner)))))
c) 修改 square-limit 的定义,将图片的方向从向内改为向外(修改square-of-four的
几个参数):
;;; 52-square-limit.scm
(define (square-limit painter n)
(let ((combine4 (square-of-four identity flip-horiz)
flip-vect rotate180))
(combine4 (corner-split painter n))))