ch02 构造数据抽象 part03
符号数据
把符号数据作为引用看待,而不是作为表达式(即求值)。
引号
用单引号引用下一个对象(符号或是表):
(define a 1) (define b 2) (list a b) ;; (1 2) (list 'a 'b) ;; (a b) (list 'a b) ;; (a 2)
也可以用于复合对象:
(car '(a b c)) ;; a (cdr '(a b c)) ;; (b c)
符号的简写
引号可以用更加符合scheme表的形式来定义:
-
'a相当于(quote a)。 -
空表
nil可以用简写'()来表示。
eq?检查符号是否相同
操作eq?检查两个符号是否为相同的符号(同样的字符且顺序相同)。
memq检查表中是否包含指定符号
(define (memq item x)
(cond ((null? x) false)
((eq? item (car x)) x)
(else (memq item (cdr x)))))
(memq 'apple '(pear banana prune)) ;; false
(memq 'apple '(x (apple sauce) y apple pear)) ;; (apple pear)
练习 2.53
求下列表达式的值:
(list 'a 'b 'c) ;Value 11: (a b c) (list (list 'george)) ;Value 12: ((george)) (cdr '((x1 x2) (y1 y2))) ;Value 13: ((y1 y2)) (cadr '((x1 x2) (y1 y2))) ;Value 14: (y1 y2) (pair? (car '(a short list))) ;Value: #f (memq 'red '((red shoes) blue socks))) ;Value: #f (memq 'red '(red shoes blue socks)) ;Value 15: (red shoes blue socks)
练习 2.54 检查两个表符号相同
元素一样,顺序也一样,则两个表equal?:
-
a与b是否equal? -
如果都是符号,两个符号是否
equal?? -
如果都是表,
(car a)和(car b)是否相等?(car a)和(car b)是否也相等?
;;; 54-equal.scm
(define (equal? x y)
(cond ((and (symbol? x) (symbol? y))
(symbol-equal? x y))
((and (list? x) (list? y))
(list-equal? x y))
(else
(error "Wrong type input x and y -- EQUAL?" x y))))
(define (symbol-equal? x y)
(eq? x y))
(define (list-equal? x y)
(cond ((and (null? x) (null? y)) ; 空表
#t)
((or (null? x) (null? y)) ; 长度不同的表
#f)
((equal? (car x) (car y)) ; 对比 car 部分
(equal? (cdr x) (cdr y))) ; 递归对比 cdr 部分
(else
#f)))
equal?的定义书上有详细的描述了,一个需要注意的地方是对空列表和长度不同的列表
的处理。
另外,equal?函数使用了symbol?函数和list?函数对输入类型进行检测,检查它们
是否是一个符号或者列表:
(list? (list 1 2 3)) ;Value: #t (list? 3) ;Value: #f (symbol? 'symbol) ;Value: #t (symbol? 3) ;Value: #f
测试:
(load "54-equal.scm") (equal? 'symbol 'symbol) ;Value: #t (equal? 'symbol 'another-symbol) ;Value: #f (equal? (list 'a 'b 'c) (list 'a 'b 'c)) ;Value: #t (equal? (list 'a) (list 'a 'b 'c)) ;Value: #f
练习 2.55
为何:
(car ''abracadabra)
的结果是quote?
符号'在求值时会被替换成quote特殊形式,因此,求值:
(car ''abracadabra)
实际上就是求值:
(car '(quote abracadabra))
因此car取出的是第一个quote的car部分,而这个car部分就是'quote,
所以返回值就是quote:
(car ''abracadabra) ;Value: quote
实例:符号求导
符号求导正是符号操作的典型应用场景。
对抽象数据的求导程序
\[ \begin{equation} \begin{split} \frac{dc}{dx} &= 0 \quad \quad \text{当$c$是一个常量,或是一个与$x$不相同的变量} \\ \frac{dx}{dx} &= 1 \\ \frac{d(u + v)}{dx} &= \frac{du}{dx} + \frac{dv}{dx} \\ \frac{d(uv)}{dx} &= u(\frac{dv}{dx}) + v(\frac{du}{dx}) \end{split} \end{equation} \]最后两条规则具有递归性质:
- 导数分解为两个导数项相加
- 然后每项可以再分解
- 最后分解为常量或是变量
定义一些基本的过程操作与谓词(以后会介绍具体的实现):
| 操作 | 说明 |
|---|---|
(number? e)
|
\(e\)是否是数字 |
(variable? e)
|
\(e\)是否是变量 |
(same-variable? v1 v2)
|
\(v1\)和\(v2\)是否相等 |
(sum? e)
|
\(e\)是否是和式 |
(addend e)
|
\(e\)的被加数 |
(augend e)
|
\(e\)的加数 |
(make-sum a1 a2)
|
把\(a1\)和\(a2\)构成和式 |
(product? e)
|
\(e\)是否是乘式 |
(multiplier e)
|
\(e\)的被乘数 |
(multiplicand e)
|
\(e\)的乘数 |
(make-product m1 m2)
|
把\(m1\)和\(m2\)做乘式 |
有了以上的基础方法,各种求导规则用下面的过程deriv表达出来,它实现一个完整的
求导方法:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type -- DERIV" exp))))
代数表达式的表示
基本操作的实现
用前缀形式,如\((a * x + b)\)用代码(+ (* a x) b)表示。
之前那些基本过程和谓词的实现:
-
变量就是符号,所以用
symbol?判断是否是变量:
(define (variable? x) (symbol? x))
-
两个变量是否相应就是两个符号是否
eq?:
(define (same-variable? v1 v2) (and (variable? v1) (variable? v2) (eq? v1 v2)))
- 和式与乘式都构造为表:
(define (make-sum a1 a2) (list '+ a1 a2)) (define (make-product m1 m2) (list '* m1 m2))
-
第一个符号为
+表示为和式:
(define (sum? x) (and (pair? x) (eq? (car x) '+)))
- 被加数是和式里的第二元素:
(define (addend s) (cadr s))
- 加数是和式里的第三个元素:
(define (augend s) (caddr s))
-
第一个元素为
*表示为乘式:
(define (product? x) (and (pair? x) (eq? (car x) '*)))
- 被乘数是乘式里的第二个元素:
(define (multiplier p) (cadr p))
- 乘数是乘式里的第三个元素:
(define (multiplicand p) (caddr p))
现在结合之前的deriv过程求导程序就可以工作了,例如:
(deriv '(+ x 3) 'x) ;; (+ 1 0)
(deriv '(* x y) 'x) ;; (+ (* x 0) (* 1 y))
(deriv '(* (* x y) (+ x 3)) 'x) ;; (+ (* (* x y) (+ 1 0))
;; (* (+ (* x 0) (* 1 y))
;; (+ x 3)))
化简操作
这里还缺少化简操作,比如:
\[ \begin{equation} \begin{split} \frac{d(xy)}{dx} &= x \cdot 0 + 1 \cdot y \end{split} \end{equation} \] \[ \begin{equation} \begin{split} x \cdot 0 &= 0 \end{split} \end{equation} \] \[ \begin{equation} \begin{split} 1 \cdot y &= y \end{split} \end{equation} \] \[ \begin{equation} \begin{split} 0 + y = y \end{split} \end{equation} \]和之前的有理数化简一样,可以把化简操作放到构造方法阶段。
make-sum构造和式时发现有一个对象是\(0\),就直接返回另一个对象:
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list '+ a1 a2))))
=number?检查表达式是否等于一个指定的数字:
(define (=number? exp num) (and (number? exp) (= exp num)))
make-product构造乘法时,特殊处理乘\(0\)和乘\(1\)的情况:
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list '* m1 m2))))
在简化以后再看之前三个例子:
(deriv '(+ x 3) 'x) ;; 1 (deriv '(* x y) 'x) ;; y (deriv '(* (* x y) (+ x 3)) 'x) ;; (+ (* x y) (* y (+ x 3)))
注意第三个例子的结果还是不理解,还有很多要改进的地方。
练习 2.56 幂次运算的求导
根据运算法则:
\[ \begin{equation} \begin{split} \frac{d(u^n)}{dx} = nu^{n-1}\Big(\frac{d(u)}{dx}\Big) \end{split} \end{equation} \]其中任何东西的\(0\)次幂都是\(1\),而\(1\)次幂是它自身。
给程序deriv添加exponentiation?、base、exponent和make-exponentiation。
;;; 56-deriv.scm
(define (deriv exp var)
(cond ((number? exp)
0)
((variable? exp)
(if (same-variable? exp var)
1
0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
((exponentiation? exp) ; 新增
(let ((n (exponent exp)) ;
(u (base exp))) ;
(make-product ;
n ;
(make-product ;
(make-exponentiation ;
u ;
(- n 1)) ;
(deriv u var))))) ;
(else
(error "unknown expression type -- DERIV" exp))))
;; exponentiation
(define (make-exponentiation base exponent) ; 新增
(cond ((= exponent 0) ;
1) ;
((= exponent 1) ;
base) ;
(else ;
(list '** base exponent)))) ;
;
(define (exponentiation? x) ;
(and (pair? x) ;
(eq? (car x) '**))) ;
;
(define (base exp) ;
(cadr exp)) ;
;
(define (exponent exp) ;
(caddr exp)) ;
;; number
(define (=number? exp num)
(and (number? exp)
(= exp num)))
;; variable
(define (variable? x)
(symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1)
(variable? v2)
(eq? v1 v2)))
;; sum
(define (make-sum a1 a2)
(cond ((=number? a1 0)
a2)
((=number? a2 0)
a1)
((and (number? a1) (number? a2))
(+ a1 a2))
(else
(list '+ a1 a2))))
(define (sum? x)
(and (pair? x)
(eq? (car x) '+)))
(define (addend s)
(cadr s))
(define (augend s)
(caddr s))
;; product
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0))
0)
((=number? m1 1)
m2)
((=number? m2 1)
m1)
((and (number? m1) (number? m2))
(* m1 m2))
(else
(list '* m1 m2))))
(define (product? x)
(and (pair? x)
(eq? (car x) '*)))
(define (multiplier p)
(cadr p))
(define (multiplicand p)
(caddr p))
测试:
1 ]=> (load "56-deriv.scm") ;Loading "56-deriv.scm"... done ;Value: multiplicand 1 ]=> (deriv '(** x 0) 'x) ;Value: 0 1 ]=> (deriv '(** x 1) 'x) ;Value: 0 1 ]=> (deriv '(** x 2) 'x) ;Value 11: (* 2 x) 1 ]=> (deriv '(** x 3) 'x) ;Value 12: (* 3 (** x 2))
练习 2.57 加法和乘法可以处理多项
强化求导运算,让加法和乘法可以处理多项,如:
(deriv '(* x y (+ x 3)) 'x)
新的加法处理函数定义如下:
;;; 57-sum.scm
(load "57-single-operand.scm")
(define (make-sum a1 . a2)
(if (single-operand? a2)
(let ((a2 (car a2)))
(cond ((=number? a1 0)
a2)
((=number? a2 0)
a1)
((and (number? a1) (number? a2))
(+ a1 a2))
(else
(list '+ a1 a2))))
(cons '+ (cons a1 a2))))
(define (sum? x)
(and (pair? x)
(eq? (car x) '+)))
(define (addend s)
(cadr s))
(define (augend s)
(let ((tail-operand (cddr s)))
(if (single-operand? tail-operand)
(car tail-operand)
(apply make-sum tail-operand))))
新的乘法处理函数定义如下:
;;; 57-product.scm
(load "57-single-operand.scm")
(define (make-product m1 . m2)
(if (single-operand? m2)
(let ((m2 (car m2)))
(cond ((or (=number? m1 0) (=number? m2 0))
0)
((=number? m1 1)
m2)
((=number? m2 1)
m1)
((and (number? m1) (number? m2))
(* m1 m2))
(else
(list '* m1 m2))))
(cons '* (cons m1 m2))))
(define (product? x)
(and (pair? x)
(eq? (car x) '*)))
(define (multiplier p)
(cadr p))
(define (multiplicand p)
(let ((tail-operand (cddr p)))
(if (single-operand? tail-operand)
(car tail-operand)
(apply make-product tail-operand))))
deriv 的大部分代码和书本 100 页的一样,没有改动:
;;; 57-deriv.scm
(load "57-sum.scm")
(load "57-product.scm")
(define (deriv exp var)
(cond ((number? exp)
0)
((variable? exp)
(if (same-variable? exp var)
1
0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type -- DERIV" exp))))
;; number
(define (=number? exp num)
(and (number? exp)
(= exp num)))
;; variable
(define (variable? x)
(symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1)
(variable? v2)
(eq? v1 v2)))
表示的变更:
为了让make-product和make-sum支持等于或多于两个参数,make-product和
make-sum使用了书本之前介绍过的点号参数形式:
1 ]=> (load "57-product.scm") ;Loading "57-product.scm"... ; Loading "57-single-operand.scm"... done ;... done ;Value: multiplicand 1 ]=> (make-product 'x 'y) ;Value 17: (* x y) 1 ]=> (make-product 'x 'y 'z) ;Value 18: (* x y z) 1 ]=> (load "57-sum.scm") ;Loading "57-sum.scm"... ; Loading "57-single-operand.scm"... done ;... done ;Value: augend 1 ]=> (make-sum 'x 'y 'z) ;Value 19: (+ x y z)
在每次调用make-product或者make-sum时,single-operand都会检查第二个参数
是否只有单个操作符:
如果传入的是参数是单个操作符,那么处理方式和之前一样,使用list组合,如果是
多个操作符的话,那么使用 cons 组合(因为第二个参数是列表)。
选择函数的变更
为了适应新的多操作符的表示,处理乘法的选择函数和处理加法的选择函数都做了不同的 修改:
multiplier和addend的定义还是和以前一样,都是取出计算的第一个操作符;
而multiplicand和augend在处理多操作符的时候,会先递归地将一个多操作符的
表达式先转换成一系列两个参数的运算表达式。
举个例子,在求值(multiplicand (make-product 'x 'y 'z))的时候,以下调用被执行:
(multiplicand (make-product 'x 'y 'z)) (multiplicand (make-product 'x 'y 'z)) (multiplicand 'x (make-product 'y 'z))
也即是,我们将一个三操作符的表达式 (* x y z)转换成了'(* x (* y z)),这样
就可以在不改动deriv的情况下进行多操作符的运算处理了。
测试
1 ]=> (load "57-deriv.scm") ;Loading "57-deriv.scm"... ; Loading "57-sum.scm"... ; Loading "57-single-operand.scm"... done ; ... done ; Loading "57-product.scm"... ; Loading "57-single-operand.scm"... done ; ... done ;... done ;Value: same-variable? 1 ]=> (deriv '(* x y (+ x 3)) 'x) ;Value 20: (+ (* x y) (* y (+ x 3)))
练习 2.58 改用中缀表达式
把加法与乘法改为中缀表达式。
a) 先设定加法与乘法只接收两个参数。
将加法的计算函数改成中序表示:
;;; 58-sum.scm
(define (make-sum a1 a2)
(cond ((=number? a1 0)
a2)
((=number? a2 0)
a1)
((and (number? a1) (number? a2))
(+ a1 a2))
(else
(list a1 '+ a2)))) ; 修改
(define (sum? x)
(and (pair? x)
(eq? (cadr x) '+))) ; 修改
(define (addend s)
(car s)) ; 修改
(define (augend s)
(caddr s))
将加法的计算函数改成中序表示:
;;; 58-product.scm
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0))
0)
((=number? m1 1)
m2)
((=number? m2 1)
m1)
((and (number? m1) (number? m2))
(* m1 m2))
(else
(list m1 '* m2)))) ; 修改
(define (product? x)
(and (pair? x)
(eq? (cadr x) '*))) ; 修改
(define (multiplier p)
(car p)) ; 修改
(define (multiplicand p)
(caddr p))
deriv 的代码和书本 100 页给出的一样,不必修改:
;;; 58-deriv.scm
(load "58-sum.scm")
(load "58-product.scm")
(define (deriv exp var)
(cond ((number? exp)
0)
((variable? exp)
(if (same-variable? exp var)
1
0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type -- DERIV" exp))))
;; number
(define (=number? exp num)
(and (number? exp)
(= exp num)))
;; variable
(define (variable? x)
(symbol? x))
(define (same-variable? v1 v2)
(and (variable? v1)
(variable? v2)
(eq? v1 v2)))
测试:
1 ]=> (load "58-deriv.scm") ;Loading "58-deriv.scm"... ; Loading "58-sum.scm"... done ; Loading "58-product.scm"... done ;... done ;Value: same-variable? 1 ]=> (make-product 'x 'y) ;Value 11: (x * y) 1 ]=> (make-sum 'x 'y) ;Value 12: (x + y) 1 ]=> (deriv '((x * y) * (x + 3)) 'x) ;Value 13: ((x * y) + (y * (x + 3)))
b) 允许标准代数写法连接多个数,如:\((x + 3 \cdot (x + y +2))\)
如果允许使用标准代数写法的话,那么我们就没办法只是通过修改谓词、选择函数和
构造函数来达到正确计算求导的目的,因为这必须要修改deriv函数,提供符号的优先级
处理功能。
比如说,对于输入$x + y \cdot z),有两种可能的求导顺序会产生(称之为二义性文法)
,一种是(x + y) * z,另一种是x + (y * z);对于求导计算来说,后一种顺序才是
正确的,但是这种顺序必须通过修改deriv来提供,只是修改谓词、选择函数和构造函数
是没办法达到调整求导顺序的目的的。
如果只是简单针对这个问题:
(define (sum? x)
(if (null? x)
#f
(or (eq? (car x) '+) (sum? (cdr x)))))
(define (addend s)
(define (addend-help s)
(if (eq? (car s) '+)
'()
(cons (car s) (addend-help (cdr s)))))
(if (eq? (cadr s) '+)
(car s)
(addend-help s)))
(define (augend s)
(define (augend-help s)
(if (eq? (car s) '+)
(cdr s)
(augend-help (cdr s))))
(let ((a (augend-help s)))
(if (= (length a) 1)
(car a)
a)))
只需要修改三个函数sum?、addend、augend就行了。
其他解法:
对于只用+和*的表达式,不用添加其他函数只要修改3个函数就可以了, addend, augend, multiplicand. 把整个表达式看成一个和式,如果有+的话。 addend就是从头到+号,augend就是从+号到最后。反复取出和式,子表达式就只剩连乘。 multiplier不变。multiplicand就是从第一个乘号到表达式最后。其他所有函数都不用改。
Baptiste ZHANG 也是这个思路。
高逼格的思路就是写个分析器,http://kelvinh.github.io/wiki/sicp/#sec-2-58。
实例:集合的表示
集合作为未排序的表
element-of-set?检查元素是否为集合的成员,注意要用equal?而不是eq?来保证
集合元素不可以是符号:
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set)))))
注意这里有整表扫描,步数增长为\(\Theta (n)\)。
在这个基础上可以实现adjoin-set把对象加到集合里。返回结果是新的集合:
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set)))
这里因为调用了element-of-set,所以步数增长也是\(\Theta (n)\)。
intersection-set生成两个集合的交集。用递归的策略:
如果已知set2与set1的cdr的交集,则只要确定是否应将set1的car包含到
结果之中,而这依赖于(car set1)是否也在set2里。
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set? (car set1) set2)
(cons (car set1)
(intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))
这里涉及两个列表,频数增长为\(\Theta (n^2)\)。
练习 2.59 实现union-set生成并集
(define (union-set s1 s2)
(if (null? s1)
s2
(adjoin-set (car s1) (union-set (cdr s1) s2))))
练习 2.60
如果集合允许重复元素,会对效率产生什么样的影响?
集合作为排序的表
比较操作:>和<
element-of-set?可以不用扫描整个表了:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (car set)) true)
((< x (car set)) false)
(else (element-of-set? x (cdr set)))))
求交集操作intersection-set操作在有序集合上效率会更高,从\(\Theta(n^2)\)降底
为\(\Theta(n)\):
- 对于两个列表的头一个元素\(x1\)和\(x2\)如果相等,则为交集的一个元素。
-
如果\(x1 < x2\),那么由于\(x2\)是\(set2\)最小的元素,所以\(x1\)不会和\(set2\)有交集。
所以继续检查
set2与(cdr set1)。 -
如果\(x2 < x1\),继续检查
set1与(cdr set2)。
(define (intersection-set set1 set2)
(if (or (null? set1) (null? set2))
'()
(let ((x1 (car set1)) (x2 (car set2)))
(cond ((= x1 x2)
(cons x1
(intersection-set (cdr set1)
(cdr set2))))
((< x1 x2)
(intersection-set (cdr set1) set2))
((< x2 x1)
(intersection-set set1 (cdr set2)))))))
练习 2.61 实现有序列表的adjoin-set
;;; 61-adjoin-set.scm
(define (adjoin-set x set)
(if (null? set)
(list x)
(let ((current-element (car set))
(remain-element (cdr set)))
(cond ((= x current-element)
set)
((> x current-element)
(cons current-element
(adjoin-set x remain-element)))
((< x current-element)
(cons x set))))))
adjoin-set遍历并使用cons重新组合整个表,并在重新组合的过程中将x加入到
集合中去,这个程序的复杂度为\(\Theta(n)\)。
利用已排序元素的表示,平均每次只需要对表内的一半元素进行查找,就能完成添加新元素 的任务。
1 ]=> (load "61-adjoin-set.scm") ;Loading "61-adjoin-set.scm"... done ;Value: adjoin-set 1 ]=> (adjoin-set 1 '()) ; 空表 ;Value 11: (1) 1 ]=> (adjoin-set 3 (list 1 2 3)) ; x 已经存在于 set ;Value 12: (1 2 3) 1 ]=> (adjoin-set 3 (list 1 2 4 5)) ; x 不存在于 set ;Value 13: (1 2 3 4 5)
另一种adjoin-set实现
实现adjoin-set的另一种方法是,将新元素转换成一个包含单元素的集合
(只有一个元素的列表),然后将两个集合进行union-set操作:
;;; 61-another-adjoin-set.scm
(load "62-union-set.scm")
(define (adjoin-set x set)
(union-set (list x) set))
其中union-set函数来自 练习 2.62,这个adjoin-set实现的复杂度也是\(\Theta(n)\)。
1 ]=> (load "61-another-adjoin-set.scm") ;Loading "61-another-adjoin-set.scm"... ; Loading "62-union-set.scm"... done ;... done ;Value: adjoin-set 1 ]=> (adjoin-set 1 '()) ; 空集 ;Value 11: (1) 1 ]=> (adjoin-set 3 (list 1 2 3)) ; 元素已存在 ;Value 12: (1 2 3) 1 ]=> (adjoin-set 3 (list 1 2 4 5)) ; 元素不存在 ;Value 13: (1 2 3 4 5)
练习 2.62 实现有序集合上的union-set
实现有序集合上的union-set上的\(\Theta(n)\)实现。
;;; 62-union-set.scm
(define (union-set set another)
(cond ((and (null? set) (null? another))
'())
((null? set)
another)
((null? another)
set)
(else
(let ((x (car set)) (y (car another)))
(cond ((= x y)
(cons x (union-set (cdr set) (cdr another))))
((< x y)
(cons x (union-set (cdr set) another)))
((> x y)
(cons y (union-set set (cdr another)))))))))
这个union-set要处理多个情况:
- 如果两个输入表都是空表,那么返回空表。
- 如果两个输入表其中一个为空表,那么返回另外一个表。
- 如果两个输入表都不为空,那么取出这两个表的第一个元素,通过对比元素来决定将 它们放到结果表的那个位置上。
另一个值得一说的情况是,当一个表比另一个表长的时候,多出来的表的剩余元素会被
cons直接连上,也即是,union-set的执行步数由较短的输入列表的长度决定。
以下展开式说明了这样一个例子:
(union-set (list 1 2) (list 1 3 5 7 9)) (cons 1 (union (list 2) (list 3 5 7 9))) (cons 1 (cons 2 (union '() (list 3 5 7 9)))) (cons 1 (cons 2 (list 3 5 7 9))) '(1 2 3 5 7 9)
1 ]=> (load "62-union-set.scm") ;Loading "62-union-set.scm"... done ;Value: union-set 1 ]=> (union-set '() (list 1 2 3)) ;Value 13: (1 2 3) 1 ]=> (union-set (list 1 2 3) (list 1 3 5)) ;Value 11: (1 2 3 5) 1 ]=> (union-set (list 1 2 3) (list 1 3 5 7 9)) ;Value 12: (1 2 3 5 7 9)
集合作为二叉树
实现为三个元素的表:本节点、左子树,右子树。比当前结点小的在左子树, 大的在右子树。查找步数增长为\(\Theta(log n)\)
(define (entry tree) (car tree)) (define (left-branch tree) (cadr tree)) (define (right-branch tree) (caddr tree)) (define (make-tree entry left right) (list entry left right))
实现element-of-set?:
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (entry set)) true)
((< x (entry set))
(element-of-set? x (left-branch set)))
((> x (entry set))
(element-of-set? x (right-branch set)))))
实现adjoin-set:
(define (adjoin-set x set)
(cond ((null? set) (make-tree x '() '()))
((= x (entry set)) set)
((< x (entry set))
(make-tree (entry set)
(adjoin-set x (left-branch set))
(right-branch set)))
((> x (entry set))
(make-tree (entry set)
(left-branch set)
(adjoin-set x (right-branch set))))))
注意:这里的树没有保持平衡。
练习 2.63 树转为列表
树转为表方法一:
(define (tree->list-1 tree)
(if (null? tree)
'()
(append (tree->list-1 (left-branch tree))
(cons (entry tree)
(tree->list-1 (right-branch tree))))))
树转为表方法二:
(define (tree->list-2 tree)
(define (copy-to-list tree result-list)
(if (null? tree)
result-list
(copy-to-list (left-branch tree)
(cons (entry tree)
(copy-to-list (right-branch tree)
result-list)))))
(copy-to-list tree '()))
a)
从前面的测试部分可以看出,对于同一棵树,tree->list-1和tree->list-2都生成
同一个列表。
对于不同形状但是包含的元素相同的多棵树,tree->list-1和tree->list-2也都生成
同一个列表。
b)
要了解两个函数的执行效率,最好的办法就是展开两个函数对同一一棵树的执行过程。
从展开过程来看,对于节点数为 6 的树,tree->list-1需要伸展 6 次,使用 6 次
append, 以及 6 次cons,可以看出,对于大小为 n 的树,append和cons的调用
次数正比于 n。
从展开过程来看,对于节点数为 6 的树来说,tree->list-2展开 6 次,调用 6 次
copy-to-list,调用 6 次cons,可以看出,对于节点数为 n 的树,tree->list-2
调用cons和copy-to-list的次数等同于 n 。
练习 2.64 把有序表变为平衡二叉树
以下能把有序表变为平衡二叉树程序的原理是什么:
;;; 64-list-tree.scm
(load "p106-tree.scm")
(define (list->tree elements)
(car (partial-tree elements (length elements))))
(define (partial-tree elts n)
(if (= n 0)
(cons '() elts)
(let ((left-size (quotient (- n 1) 2)))
(let ((left-result (partial-tree elts left-size)))
(let ((left-tree (car left-result))
(non-left-elts (cdr left-result))
(right-size (- n (+ left-size 1))))
(let ((this-entry (car non-left-elts))
(right-result (partial-tree (cdr non-left-elts)
right-size)))
(let ((right-tree (car right-result))
(remaining-elts (cdr right-result)))
(cons (make-tree this-entry left-tree right-tree)
remaining-elts))))))))
a)
list->tree将调用partial-tree,而partial-tree每次将输入的列表分成两半
(右边可能比左边多一个元素,用作当前节点),然后组合成一个平衡树。
b)
对于列表中的每个节点,list->tree都要执行一次 make-tree (复杂度为\(\Theta(1)\))
,将这个节点和它的左右子树组合起来,因此对于长度为 n 的列表来说,list->tree的
复杂度为\(\Theta(n)\)。
练习 2.65 平衡二叉树的交集与并集操作
为了避免和所使用的辅助程序发生重名冲突,本题的intersection-set被改名为
intersection-tree,union-set被改名成union-tree。
使用树实现的\(\Theta(n)\)复杂度的intersection-tree和union-tree的步骤如下:
-
使用 练习 2.63 的
tree->list-2程序,将输入的两棵树转换成两个列表, 复杂度\(\Theta(n)\)。 -
如果要执行的是交集操作,那么使用书本 105 页的
intersection-set计算两个列表的 交集;如果要执行的是并集操作,那么使用 练习 2.62 的union-set计算两个列表的 并集;以上两个程序的复杂度都是\(\Theta(n)\)。 -
使用 练习 2.64 的
list->tree程序,将第二步操作所产生的列表转换成一棵平衡树, 复杂度为\(\Theta(n)\)。
intersection-tree和union-tree的整个过程需要使用三个复杂度为\(\Theta(n)\)的程序
,但总的复杂度还是\(\Theta(n)\),因此符合题目的要求。
intersection-tree
定义:
;;; 65-intersection-tree.scm
(load "63-tree-list-2.scm")
(load "64-list-tree.scm")
(load "p105-intersection-set.scm")
(define (intersection-tree tree another)
(list->tree
(intersection-set (tree->list-2 tree)
(tree->list-2 another))))
测试:
1 ]=> (load "65-intersection-tree.scm")
;Loading "65-intersection-tree.scm"...
; Loading "63-tree-list-2.scm"...
; Loading "p106-tree.scm"... done
; ... done
; Loading "64-list-tree.scm"...
; Loading "p106-tree.scm"... done
; ... done
; Loading "p105-intersection-set.scm"... done
;... done
;Value: intersection-tree
1 ]=> (define it (intersection-tree (list->tree '(1 2 3 4 5))
(list->tree '(1 3 5 7 9)))) ;Value: it
1 ]=> it ;Value 11: (3 (1 () ()) (5 () ()))
1 ]=> (tree->list-2 it) ;Value 12: (1 3 5)
union-tree
定义:
;;; 65-union-tree.scm
(load "62-union-set.scm")
(load "63-tree-list-2.scm")
(load "64-list-tree.scm")
(define (union-tree tree another)
(list->tree
(union-set (tree->list-2 tree)
(tree->list-2 another))))
测试:
1 ]=> (load "65-union-tree.scm")
;Loading "65-union-tree.scm"...
; Loading "62-union-set.scm"... done
; Loading "63-tree-list-2.scm"...
; Loading "p106-tree.scm"... done
; ... done
; Loading "64-list-tree.scm"...
; Loading "p106-tree.scm"... done
; ... done
;... done
;Value: union-tree
1 ]=> (define ut (union-tree (list->tree '(1 2 3 4 5))
(list->tree '(1 3 5 7 9)))) ;Value: ut
1 ]=> Ut
;Value 12: (4 (2 (1 () ()) (3 () ())) (7 (5 () ()) (9 () ())))
1 ]=> (tree->list-2 ut) ;Value 13: (1 2 3 4 5 7 9)
集合与数据检索
-
作为记录的数据结构中有一个属性
key。 -
lookup过程在没有排序的集体中查询key为指定值的记录。
(define (lookup given-key set-of-records)
(cond ((null? set-of-records) false)
((equal? given-key (key (car set-of-records)))
(car set-of-records))
(else (lookup given-key (cdr set-of-records)))))
练习 2.66 有序二叉树查询
根据数据抽象的原则,我们完全不必了解记录集合所使用的二叉树的实现细节,只要知道对于一棵树,有以下函数可以作用于它:
-
entry:取出当前节点 -
left-branch:转向树的左分支 -
right-branch:转向树的右分支 -
key:从节点中获取键
根据以上这些函数,我们可以给出相应的二叉树实现的数据库 lookup 程序:
;;; 66-lookup.scm
(define (lookup given-key tree-of-records)
(if (null? tree-of-records) ; 数据库为空,查找失败
#f
(let ((entry-key (key (entry tree-of-records)))) ; 获取当前节点的键
(cond ((= given-key entry-key) ; 对比当前节点的键和给定的查找键
(entry tree-of-records)) ; 决定查找的方向
((> given-key entry-key)
(lookup given-key (right-branch tree-of-records)))
((< given-key entry-key)
(lookup given-key (left-branch tree-of-records)))))))
lookup实际上就是树的包装程序了。
以下是一棵假设的树的例子(以人名记录为例):
(7 "John")
/ \
/ \
(3 "Mary") (19 "Tom")
/ \
(1 "Peter") (5 "Jack")
2.3.4 实现:Huffman编码树
字符的编码长度不固定,使用频率高的字符编码短,频率低的编码长。
例:对于消息:BACADAEAFABBAAAGAH,涉及8个字符A B C D E F G H。
按出现频率给每个字符加上权重,A是8,B为3,其他的都是1。
然后分配到树里,让每个节点左右两边的总权重尽量相等:
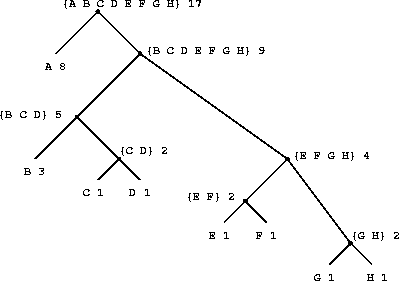
生成编码,每次向左为0,向右为1。如D的编码为1011。
从编码生成文字可以按图向下走,读到0向左,读到1向右,遇到叶结点表示读到字符,
然后回到根节点。如10001010生成BAC。
生成Huffman树
- 从集合里取出两个权生最低的节点,归并它们生成新节点(权重是两个节点之各,左右 节点分别是这两个节点)。
- 用这个新节点替代原来集合里的那两个节点。
- 重复,直到只有一个节点。
| Initial leaves | {(A 8) (B 3) (C 1) (D 1) (E 1) (F 1) (G 1) (H 1)} |
| Merge | {(A 8) (B 3) ({C D} 2) (E 1) (F 1) (G 1) (H 1)} |
| Merge | {(A 8) (B 3) ({C D} 2) ({E F} 2) (G 1) (H 1)} |
| Merge | {(A 8) (B 3) ({C D} 2) ({E F} 2) ({G H} 2)} |
| Merge | {(A 8) (B 3) ({C D} 2) ({E F G H} 4)} |
| Merge | {(A 8) ({B C D} 5) ({E F G H} 4)} |
| Merge | {(A 8) ({B C D E F G H} 9)} |
| Final merge | {({A B C D E F G H} 17)} |
这样的过程中每一次选出的最小节点并不要求一样,顺序也不一定一样(是左是右并不影响 效率)。
Huffman树的表示
节点表示为:包含符号的leaf、叶中符号和权重的表
(define (make-leaf symbol weight) (list 'leaf symbol weight)) (define (leaf? object) (eq? (car object) 'leaf)) (define (symbol-leaf x) (cadr x)) (define (weight-leaf x) (caddr x))
树表示为:左分支、右分支、符号集合、权重。结合2.2.1节中的append过程:
(define (make-code-tree left right)
(list left
right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))
相配套的选择函数为:
(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
(if (leaf? tree)
(list (symbol-leaf tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree)
(weight-leaf tree)
(cadddr tree)))
由于一般节点与叶节点是不同的数据结构,这问题涉及到2.4节与2.5节讨论的「通过过程」 方案。
解码过程
解码的过程需要两个参数:0/1表和一个Huffman树
(define (decode bits tree)
(define (decode-1 bits current-branch)
(if (null? bits)
'()
(let ((next-branch
(choose-branch (car bits) current-branch)))
(if (leaf? next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch)))))
(decode-1 bits tree))
(define (choose-branch bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(else (error "bad bit -- CHOOSE-BRANCH" bit))))
整个过程就是按表从上向下选择左右爬树,到到编码以后回到根节点再重复。
带权重元素的集合
改进练习2.61增加元素到集合的过程,在增加地过程是检查权重。
(define (adjoin-set x set)
(cond ((null? set) (list x))
((< (weight x) (weight (car set))) (cons x set))
(else (cons (car set)
(adjoin-set x (cdr set))))))
下面的过程以符号与权重组成的对偶的表为参数,如((A 4) (B 2) (C 1) (D 1))。
构造出有序的集合,以便Huffman算法做归并:
(define (make-leaf-set pairs)
(if (null? pairs)
'()
(let ((pair (car pairs)))
(adjoin-set (make-leaf (car pair) ; symbol
(cadr pair)) ; frequency
(make-leaf-set (cdr pairs))))))
练习 2.67
通过以下的编码程序和消息:
(define sample-tree
(make-code-tree (make-leaf 'A 4)
(make-code-tree
(make-leaf 'B 2)
(make-code-tree (make-leaf 'D 1)
(make-leaf 'C 1)))))
(define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))
请定义一个解码方法来解码。
定义出编码树,并解码给定的消息:
1 ]=> (load "p112-huffman.scm")
;Loading "p112-huffman.scm"... done
;Value: weight
1 ]=> (load "p113-decode.scm")
;Loading "p113-decode.scm"...
; Loading "p112-huffman.scm"... done
;... done
;Value: choose-branch
1 ]=> (define tree (make-code-tree (make-leaf 'A 4)
(make-code-tree (make-leaf 'B 2)
(make-code-tree (make-leaf 'D 1)
(make-leaf 'C 1)))))
;Value: tree
1 ]=> (define msg '(0 1 1 0 0 1 0 1 0 1 1 1 0)) ;Value: msg
1 ]=> (decode msg tree) ;Value 11: (a d a b b c a)
以下是前面的测试用到的代码,分别是书本 112 页的huffman表示以及 113 页的
decode函数:
;;; p112-huffman.scm
;; leaf
(define (make-leaf symbol weight)
(list 'leaf symbol weight))
(define (leaf? object)
(eq? (car object) 'leaf))
(define (symbol-leaf x)
(cadr x))
(define (weight-leaf x)
(caddr x))
;; tree
(define (make-code-tree left right)
(list left
right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))
(define (left-branch tree)
(car tree))
(define (right-branch tree)
(cadr tree))
(define (symbols tree)
(if (leaf? tree)
(list (symbol-leaf tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree)
(weight-leaf tree)
(cadddr tree)))
;;; p113-decode.scm
(load "p112-huffman.scm")
(define (decode bits tree)
(define (decode-1 bits current-branch)
(if (null? bits)
'()
(let ((next-branch
(choose-branch (car bits) current-branch)))
(if (leaf? next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch)))))
(decode-1 bits tree))
(define (choose-branch bit branch)
(cond ((= bit 0)
(left-branch branch))
((= bit 1)
(right-branch branch))
(else
(error "bad bit -- CHOOSE-BRANCH" bit))))
练习 2.68
encode以一个消息和一个树为参数,完成编码工作。
(define (encode message tree)
(if (null? message)
'()
(append (encode-symbol (car message) tree)
(encode (cdr message) tree))))
请实现其中用到的encode-symbol过程。它按照树生成符号的编码。
假设我们已经有了可运行的 encode 函数,那么对于 练习 2.67 的 sample-tree :
(define sample-tree
(make-code-tree (make-leaf 'A 4)
(make-code-tree
(make-leaf 'B 2)
(make-code-tree (make-leaf 'D 1)
(make-leaf 'C 1)))))
表达式(encode (list 'A 'D 'A 'B 'B 'C 'A) sample-tree)的执行过程应该是:
(encode (list 'A 'D 'A 'B 'B 'C 'A) sample-tree)
(append (encode-symbol 'A sample-tree)
(encode (list 'D 'A 'B 'B 'C 'A) sample-tree))
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'D sample-tree)
(encode (list 'A 'B 'B 'C 'A) sample-tree)))
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'D sample-tree)
(append (encode-symbol 'A sample-tree)
(encode (list 'B 'B 'C 'A) sample-tree))))
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'D sample-tree)
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'B sample-tree)
(encode (list 'B 'C 'A sample-tree))))))
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'D sample-tree)
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'B sample-tree)
(append (encode-symbol 'B sample-tree)
(encode (list 'C 'A) sample-tree))))))
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'D sample-tree)
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'B sample-tree)
(append (encode-symbol 'B sample-tree)
(append (encode-symbol 'C sample-tree)
(encode (list 'A) sample-tree)))))))
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'D sample-tree)
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'B sample-tree)
(append (encode-symbol 'B sample-tree)
(append (encode-symbol 'C sample-tree)
(append (encode-symbol 'A sample-tree)
(encode '() sample-tree))))))))
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'D sample-tree)
(append (encode-symbol 'A sample-tree)
(append (encode-symbol 'B sample-tree)
(append (encode-symbol 'B sample-tree)
(append (encode-symbol 'C sample-tree)
(append (encode-symbol 'A sample-tree)
'())))))))
(append (list 0) ; A
(append (list 1 1 0) ; D
(append (list 0) ; A
(append (list 1 0) ; B
(append (list 1 0) ; B
(append (list 1 1 1) ; C
(append (list 0) ; A
'())))))))
'( 0 1 1 0 0 1 0 1 0 1 1 1 0)
其中encode-symbol就是题目要我们写出的函数,它的返回值是相应的符号的编码位。
encode-symbol
对于sample-tree,可以用一个图形来表示它:
[A B D C]
*
/ \
A \
* [B D C]
/ \
B \
* [D C]
/ \
D C
要使用encode-symbol函数获取给定符号的编码位,其实就是要求我们在给定的树中查找
给定符号的叶子节点,并记录下寻找过程中的左右方向,每次向左前进一层就用一个 0
表示,每次向右前进一层就用 1 表示,直到到达给定的符号所在的树叶为止。
比如说,(encode-symbol 'D sample-tree)的穿行过程就有以下步骤:
| 当前位置 | 方向 | 当前位 | 已编码信息位 |
|---|---|---|---|
| [A B D C] | 无 | 无 | 无 |
| [B D C] | 右 | 1 | 1 |
| [D C] | 右 | 1 | 11 |
| D | 左 | 0 | 110 |
有了前面的线索,现在可以给出encode-symbol的定义了:
;;; 68-encode-symbol.scm
(load "p112-huffman.scm")
(define (encode-symbol symbol tree)
(cond ((leaf? tree) ; 如果已经到达叶子节点,那么停止积累
'())
((symbol-in-tree? symbol (left-branch tree)) ; 符号在左分支(左子树),组合起 0
(cons 0
(encode-symbol symbol (left-branch tree))))
((symbol-in-tree? symbol (right-branch tree)) ; 符号在右分支(右子树),组合起 1
(cons 1
(encode-symbol symbol (right-branch tree))))
(else ; 给定符号不存在于树,报错
(error "This symbol not in tree: " symbol))))
(define (symbol-in-tree? given-symbol tree)
(not
(false?
(find (lambda (s) ; 使用 find 函数,在树的所有符号中寻找给定符号
(eq? s given-symbol))
(symbols tree))))) ; 取出树中的所有符号
测试encode-symbol:
1 ]=> (load "p112-huffman.scm")
;Loading "p112-huffman.scm"... done
;Value: weight
1 ]=> (define sample-tree
(make-code-tree (make-leaf 'A 4)
(make-code-tree
(make-leaf 'B 2)
(make-code-tree (make-leaf 'D 1)
(make-leaf 'C 1)))))
;Value: sample-tree
1 ]=> (load "68-encode-symbol.scm")
;Loading "68-encode-symbol.scm"...
; Loading "p112-huffman.scm"... done
;... done
;Value: symbol-in-tree?
1 ]=> (encode-symbol 'D sample-tree) ;Value 14: (1 1 0)
1 ]=> (encode-symbol 'A sample-tree) ;Value 15: (0)
1 ]=> (encode-symbol 'hello sample-tree) ; 符号不存在于树
;This symbol not in tree: hello
;To continue, call RESTART with an option number:
; (RESTART 1) => Return to read-eval-print level 1.
2 error>
测试symbol-in-tree?:
1 ]=> (symbol-in-tree? 'a sample-tree) ;Value: #t 1 ]=> (symbol-in-tree? 'hello sample-tree) ;Value: #f
encode
有了encode-symbol,现在可以给出完整的encode定义了:
;;; 68-encode.scm
(load "68-encode-symbol.scm")
(define (encode message tree)
(if (null? message)
'()
(append (encode-symbol (car message) tree)
(encode (cdr message) tree))))
测试:
1 ]=> (load "68-encode.scm") ;Loading "68-encode.scm"... ; Loading "68-encode-symbol.scm"... ; Loading "p112-huffman.scm"... done ; ... done ;... done ;Value: encode 1 ]=> (encode (list 'A 'D 'A 'B 'B 'C 'A) sample-tree) ;Value 16: (0 1 1 0 0 1 0 1 0 1 1 1 0)
See also:find 函数的手册 。
练习 2.69
以下程序以符号和权重的对偶的列表为参数:
(define (generate-huffman-tree pairs) (successive-merge (make-leaf-set pairs)))
-
make-leaf-set是之前给出的程序,它把对偶表变为叶节点的有序集 -
successive-merge需要实现,它使用make-code-tree反复归并集合中最小权重的, 直到只剩下一个元素(即Huffman树)。
在书本 111 到 112 页的「生成 Huffman 树」小节,已经很详细地说明了 Huffman 树的
生成过程了,generate-huffman-tree就是这一过程的程序化表示:
;;; 69-generate-huffman-tree.scm
(load "p113-adjoin-set.scm")
(load "p114-make-leaf-set.scm")
(define (generate-huffman-tree pairs)
(successive-merge (make-leaf-set pairs)))
(define (successive-merge ordered-set)
(cond ((= 0 (length ordered-set))
'())
((= 1 (length ordered-set))
(car ordered-set))
(else
(let ((new-sub-tree (make-code-tree (car ordered-set)
(cadr ordered-set)))
(remained-ordered-set (cddr ordered-set)))
(successive-merge (adjoin-set new-sub-tree remained-ordered-set))))))
因为successive-merge接受的是有序集合(按权重值从低到高排列,用一个列表表示),
所以我们可以这样来生成 Huffman 树:
- 如果集合的大小为 0 ,那么返回空表 '()
- 如果集合的大小为 1 ,那么返回列表的 car 部分,也即是,取出列表中 (已经生成完毕)的 Huffman 树
-
如果集合的大小大于 1 ,也即是说,集合中至少有两个元素,那么根据集合已排序的
原则,列表最前面的两个元素肯定是集合所有元素中权重最少的两个,因此,调用
make-code-tree组合起这两个元素,得出新子树,并从表示集合的列表中删除 这两个元素,得出新集合,然后使用函数adjoin-tree,将新子树有序地加入到新集合 中去。 - 一直进行步骤 3 ,直到落入步骤 2 为止
以上步骤最重要的就是使用adjoin-tree保持新列表也是有序的,所以组合树的操作可以
继续有序地进行。
另外要指出的一点是,当successive-merge第一次被调用时,它接受的列表中的所有
元素都是树叶,但是之后这个列表里就既有树叶,也有树了,因为我们使用通用的weight
提取它们的权重,所以不会遇到列表中有两类元素需要处理的麻烦,这也体现了通用操作的威力。
测试:
1 ]=> (load "69-generate-huffman-tree.scm") ;Loading "69-generate-huffman-tree.scm"... ; Loading "p113-adjoin-set.scm"... ; Loading "p112-huffman.scm"... done ; ... done ; Loading "p114-make-leaf-set.scm"... ; Loading "p113-adjoin-set.scm"... ; Loading "p112-huffman.scm"... done ; ... done ; ... done ;... done ;Value: successive-merge 1 ]=> (generate-huffman-tree '((A 4) (B 2) (C 1) (D 1))) ;Value 13: ((leaf a 4) ((leaf b 2) ((leaf d 1) (leaf c 1) (d c) 2) (b d c) 4) (a b d c) 8)
练习 2.70
考虑以下单词的频率(而不是字符的频率):
| A | 2 | NA | 16 |
| BOOM | 1 | SHA | 3 |
| GET | 2 | YIP | 9 |
| JOB | 2 | WAH | 1 |
用练习 2.69中的generate-huffman-tree过重生成Huffman树,用练习 2.68中的encode
过程编码以下消息:
Get a job Sha na na na na na na na na Get a job Sha na na na na na na na na Wah yip yip yip yip yip yip yip yip yip Sha boom
生成编码树:
1 ]=> (load "69-generate-huffman-tree.scm") ;Loading "69-generate-huffman-tree.scm"... ; Loading "p113-adjoin-set.scm"... ; Loading "p112-huffman.scm"... done ; ... done ; Loading "p114-make-leaf-set.scm"... ; Loading "p113-adjoin-set.scm"... ; Loading "p112-huffman.scm"... done ; ... done ; ... done ;... done ;Value: successive-merge 1 ]=> (define tree (generate-huffman-tree '((A 1) (NA 16) (BOOM 1) (SHA 3) (GET 2) (YIP 9) (JOB 2) (WAH 1))))
对给定信息进行编码:
1 ]=> (load "68-encode.scm") ;Loading "68-encode.scm"... ; Loading "68-encode-symbol.scm"... ; Loading "p112-huffman.scm"... done ; ... done ;... done ;Value: encode 1 ]=> (define msg-1 '(Get a job)) ;Value: msg-1 1 ]=> (encode msg-1 tree) ;Value 25: (1 1 0 0 1 1 1 1 0 1 1 1 1 1) 1 ]=> (define msg-2 '(Sha na na na na na na na na)) ;Value: msg-2 1 ]=> (encode msg-2 tree) ;Value 26: (1 1 1 0 0 0 0 0 0 0 0 0) 1 ]=> (define msg-3 '(Wah yip yip yip yip yip yip yip yip yip)) ;Value: msg-3 1 ]=> (encode msg-3 tree) ;Value 27: (1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0) 1 ]=> (define msg-4 '(Sha boom)) ;Value: msg-4 1 ]=> (encode msg-4 tree) ;Value 28: (1 1 1 0 1 1 0 1 1)
计算给定信息编码所需的位数量:
1 ]=> (length (encode msg-1 tree)) ;Value: 14 1 ]=> (length (encode msg-2 tree)) ;Value: 12 1 ]=> (length (encode msg-3 tree)) ;Value: 23 1 ]=> (length (encode msg-4 tree)) ;Value: 9
编码后信息所需的二进制位数量为14 * 2 + 12 * 2 + 23 + 9 = 84,
其中msg-1和msg-2出现了两次,所以数量要乘以 2 。
如果采用定长编码,那么 8 个字符每个最少每个要占用 3 个二进制位,
而未编码的原文总长度为3 * 2 + 9 * 2 + 10 + 2 = 36,
那么使用定长编码所需的二进制位为36 * 3 = 108。
也即是说,使用 huffman 编码比使用定长编码节省了 24 个二进制位。
练习 2.71
设huffman树有\(n\)个符号,频率分别为\(1, 2, 4, \cdots , 2^{n-1}\)。 当\(n=5\)和\(n=10\)时树是什么样子?频率最高和最低的符号分别要用几位二进制?
\(n=5\)时的树(只显示相对频度,不显示数据):
*
/\
* 16
/\
* 8
/ \
* 4
/\
1 2
\(n=10\)时的树(只显示相对频度,不显示数据):
*
/\
* 512
/\
* 256
/\
* 128
/\
* 64
/\
* 32
/\
* 16
/\
* 8
/ \
* 4
/\
1 2
可以看出,对于这种类型的树,编码使用最频繁的字符需要\(1\)个二进制位, 而编码最不常用的字符需要\(n−1\)个二进制位。
练习 2.71
结合练习 2.68的编码过程,编码一个符号频数增长率是什么?
如果符号的相对频度跟 练习 2.71 所列举的一样,那么根据 练习 2.71 的结果,对于 出现最频繁的字符,每次编码它需要下降\(1\)层,而对于出现最不频繁的字符,每次编码 它需要下降\(n−1\)层。
因此,如果编码字符的次数为\(n\),那么对最频繁出现的字符进行编码的复杂度为 \(\Theta(n)\),而对最不频繁出现的字符进行编码的复杂度为\(\Theta(n^2)\) 。