Jade Dungeon

ch02 构造数据抽象 part04

抽象数据的多重表示

抽象数据的多重表示

对一个数据对象可以用多个表示的方式，用户也希望系统能处理多种表示形式。

通用型过程：可以在不止一种数据表示上操作的过程。
让过程在事有类型标记的数据对象上工作。

除了水平上的抽象屏障把不同层次的隔离开来，还有垂直的屏障隔离不同的设计实现。比如通过直角坐标形式与极坐标形式两种方式都可以实现对复数的抽象。

复数的表示

通过直角坐标形式（实部和虚部）与极坐标形式（模和幅角）两种方式都可以实现对复数的抽象。

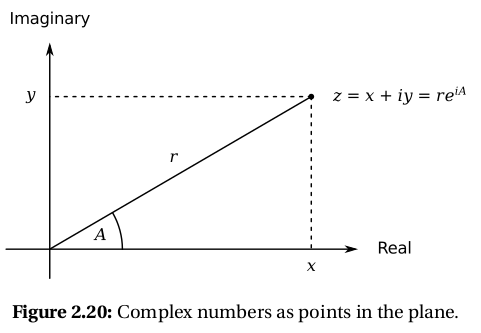
复数的加法可以归结为两个极坐标相加：

\[ \begin{equation} \begin{split} \text{实部}(z_1 + z_2) &= \text{实部}(z_1) + \text{实部}(z_2) \\ \text{虚部}(z_1 + z_2) &= \text{虚部}(z_1) + \text{虚部}(z_2) \end{split} \end{equation} \]

乘法更加适用用极坐标：

\[ \begin{equation} \begin{split} \text{模}(z_1 \cdot z_2) &= \text{模}(z_1) \cdot \text{模}(z_2) \\ \text{幅角}(z_1 \cdot z_2) &= \text{幅角}(z_1) + \text{幅角}(z_2) \end{split} \end{equation} \]

为了实现两套方案，要有四个选择函数：

real-part
imag-part
magnitude
angle

构造函数也要有两个：

make-from-real-imag
make-from-mag-ang

(make-from-real-imag (real-part z) (imag-part z))

(make-from-mag-ang (magnitude z) (angle z))

加法减法操作使用实部与虚部的方式，而乘法和除法使用模和幅角的方式：

(define (add-complex z1 z2)
  (make-from-real-imag (+ (real-part z1) (real-part z2))
                       (+ (imag-part z1) (imag-part z2))))

(define (sub-complex z1 z2)
  (make-from-real-imag (- (real-part z1) (real-part z2))
                       (- (imag-part z1) (imag-part z2))))

(define (mul-complex z1 z2)
  (make-from-mag-ang (* (magnitude z1) (magnitude z2))
                     (+ (angle z1) (angle z2))))

(define (div-complex z1 z2)
  (make-from-mag-ang (/ (magnitude z1) (magnitude z2))
                     (- (angle z1) (angle z2))))

直角坐标\((x, y)\)时与极坐标\((r, A)\)转换时需要涉及三角运算：

\[ \begin{equation} \begin{split} x &= r \cdot cos A \\ r &= \sqrt{x^2 + y^2} \\ y &= r \cdot sin A \\ A &= arctan(y, x) \end{split} \end{equation} \]

直角坐标到极坐标的转换：

(define (real-part z) (car z))

(define (imag-part z) (cdr z))

(define (magnitude z)
  (sqrt (+ (square (real-part z)) (square (imag-part z)))))

(define (angle z)
  (atan (imag-part z) (real-part z)))

(define (make-from-real-imag x y) (cons x y))

(define (make-from-mag-ang r a) 
  (cons (* r (cos a)) (* r (sin a))))

极坐标到直角坐标的转换：

(define (real-part z)
  (* (magnitude z) (cos (angle z))))

(define (imag-part z)
  (* (magnitude z) (sin (angle z))))

(define (magnitude z) (car z))

(define (angle z) (cdr z))

(define (make-from-real-imag x y) 
  (cons (sqrt (+ (square x) (square y)))
        (atan y x)))

(define (make-from-mag-ang r a) (cons r a))

带标志的数据

要用标志位来指明数据是用哪种方式实现的。

例：在这里用符号rectangular或polar。

把标记和数据一起生成带标记的数据：

(define (attach-tag type-tag contents)
  (cons type-tag contents))

从数据中取出标记：

(define (type-tag datum)
  (if (pair? datum)
      (car datum)
      (error "Bad tagged datum -- TYPE-TAG" datum)))

从数据中取出内容：

(define (contents datum)
  (if (pair? datum)
      (cdr datum)
      (error "Bad tagged datum -- CONTENTS" datum)))

分辨是直角坐标实现还是极坐标实现：

(define (rectangular? z)
  (eq? (type-tag z) 'rectangular))
  
(define (polar? z)
  (eq? (type-tag z) 'polar))

处理直角坐标实现的程序总是设置标记位为直角坐标，这了防止过程名重复，总是加上后缀rectangular：

(define (real-part-rectangular z) (car z))

(define (imag-part-rectangular z) (cdr z))

(define (magnitude-rectangular z)
  (sqrt (+ (square (real-part-rectangular z))
           (square (imag-part-rectangular z)))))

(define (angle-rectangular z)
  (atan (imag-part-rectangular z)
        (real-part-rectangular z)))

(define (make-from-real-imag-rectangular x y)
  (attach-tag 'rectangular (cons x y)))

(define (make-from-mag-ang-rectangular r a) 
  (attach-tag 'rectangular
              (cons (* r (cos a)) (* r (sin a)))))

处理极坐标程序问题设置标记为极坐标，并且过程名后缀为polar：

(define (real-part-polar z)
  (* (magnitude-polar z) (cos (angle-polar z))))

(define (imag-part-polar z)
  (* (magnitude-polar z) (sin (angle-polar z))))

(define (magnitude-polar z) (car z))

(define (angle-polar z) (cdr z))

(define (make-from-real-imag-polar x y) 
  (attach-tag 'polar
               (cons (sqrt (+ (square x) (square y)))
                     (atan y x))))

(define (make-from-mag-ang-polar r a)
  (attach-tag 'polar (cons r a)))

而每个选择函数都要在处理前检查数据实现的类型标志：

(define (real-part z)
  (cond ((rectangular? z) 
         (real-part-rectangular (contents z)))
        ((polar? z)
         (real-part-polar (contents z)))
        (else (error "Unknown type -- REAL-PART" z))))

(define (imag-part z)
  (cond ((rectangular? z)
         (imag-part-rectangular (contents z)))
        ((polar? z)
         (imag-part-polar (contents z)))
        (else (error "Unknown type -- IMAG-PART" z))))

(define (magnitude z)
  (cond ((rectangular? z)
         (magnitude-rectangular (contents z)))
        ((polar? z)
         (magnitude-polar (contents z)))
        (else (error "Unknown type -- MAGNITUDE" z))))

(define (angle z)
  (cond ((rectangular? z)
         (angle-rectangular (contents z)))
        ((polar? z)
         (angle-polar (contents z)))
        (else (error "Unknown type -- ANGLE" z))))

因为在刚才的选择函数里已经处理了不同类型的数据，所以在处理算术运算时不用考虑数据实现方式：

(define (add-complex z1 z2)
  (make-from-real-imag (+ (real-part z1) (real-part z2))
                       (+ (imag-part z1) (imag-part z2))))

最后还要考虑是要用直角坐标还是极坐标方案。一种方案是在手头有实部和虚部时用直角坐标，在有模和幅角时用极坐标：

(define (make-from-real-imag x y)
  (make-from-real-imag-rectangular x y))

(define (make-from-mag-ang r a)
  (make-from-mag-ang-polar r a))

现在一个程序已经分成了三个相互独立的模块：算术运算、直角坐标实现、极坐标实现。

数据导向和程序设计的可加性

基于类型的分配

基于类型的分配：先检查数据项的类型，然后按结果调用对应的程序。

前一节实现的带标志的复数系统。就是基于类型的分配。

基于类型的分配的缺点：

处理程序必须知道所有不同的数据表示方案。
不同处理方案的过程名不能重名。

这两个缺点导致程序界面不具有可加性。每增加一种新的表示形式，通过选择程序都需要作出修改。

基于数据导向的程序

类似一张二维表，一个维度是各种操作；另一个维度是各种表示方式。

		表示方式
		Polar	Rectangular
操作	real-part	real-part-polar	real-part-rectangular
	image-part	image-part-polar	image-part-rectangular
	magnitude	magnitude-polar	magnitude-rectangular
	angle	angle-polar	angle-rectangular

这样可以通过查表的方式找到合适的过程。也可以把一种新的数据表示方式加入系统里。 get与put过程用来处理表格操作（先不考虑实现）：

;; 以 op 和 type 两个为索引，放入 item
(put <op> <type> <item>)

;; 以 op 和 type 取出 item，反不到返回假
(get <op> <type>)

现在实现直角坐标表示方案不用考虑过程名重名，因为方法定义在内部：

(define (install-rectangular-package)

  ;; internal procedures
  
  (define (real-part z) (car z))
  
  (define (imag-part z) (cdr z))
  
  (define (make-from-real-imag x y) (cons x y))
  
  (define (magnitude z)
    (sqrt (+ (square (real-part z))
             (square (imag-part z)))))
  
  (define (angle z)
    (atan (imag-part z) (real-part z)))
  
  (define (make-from-mag-ang r a) 
    (cons (* r (cos a)) (* r (sin a))))
  
  ;; interface to the rest of the system
  
  (define (tag x) (attach-tag 'rectangular x))
  
  (put 'real-part '(rectangular) real-part)
  
  (put 'imag-part '(rectangular) imag-part)
  
  (put 'magnitude '(rectangular) magnitude)
  
  (put 'angle '(rectangular) angle)
  
  (put 'make-from-real-imag 'rectangular 
       (lambda (x y) (tag (make-from-real-imag x y))))
  
  (put 'make-from-mag-ang 'rectangular 
       (lambda (r a) (tag (make-from-mag-ang r a))))
  
  'done)

极坐标实现也是类似：

(define (install-polar-package)

  ;; internal procedures

  (define (magnitude z) (car z))

  (define (angle z) (cdr z))

  (define (make-from-mag-ang r a) (cons r a))

  (define (real-part z)
    (* (magnitude z) (cos (angle z))))

  (define (imag-part z)
    (* (magnitude z) (sin (angle z))))

  (define (make-from-real-imag x y) 
    (cons (sqrt (+ (square x) (square y)))
          (atan y x)))

  ;; interface to the rest of the system

  (define (tag x) (attach-tag 'polar x))

  (put 'real-part '(polar) real-part)

  (put 'imag-part '(polar) imag-part)

  (put 'magnitude '(polar) magnitude)

  (put 'angle '(polar) angle)

  (put 'make-from-real-imag 'polar
       (lambda (x y) (tag (make-from-real-imag x y))))

  (put 'make-from-mag-ang 'polar 
       (lambda (r a) (tag (make-from-mag-ang r a))))

  'done)

apply-generic在表格中用操作名和参数类型查找适合的过程：

(define (apply-generic op . args)
  (let ((type-tags (map type-tag args)))
    (let ((proc (get op type-tags)))
      (if proc
          (apply proc (map contents args))
          (error
            "No method for these types -- APPLY-GENERIC"
            (list op type-tags))))))

在这个基础上，各种通过的选择函数定义如下：

(define (real-part z) (apply-generic 'real-part z))
(define (imag-part z) (apply-generic 'imag-part z))
(define (magnitude z) (apply-generic 'magnitude z))
(define (angle z) (apply-generic 'angle z))

这些方法在有新表示方案时不用修改。

构造函数可以直接从表中拿出对应的构造函数来：

(define (make-from-real-imag x y)
  ((get 'make-from-real-imag 'rectangular) x y))

(define (make-from-mag-ang r a)
  ((get 'make-from-mag-ang 'polar) r a))

练习 2.73

练习 2.74

消息传递

数据导向通过查找类型的指定操作来选择合适的操作实现方案。

消息传递风格：把数据对象设想为一个实体，以「消息」的方式接收所要操作的名字。

消息传递风格的程序把每一个数据对象表示为一个过程，它把操作名字作为参数，选择合适的操作实现方案。

例如make-from-real-imag：

(define (make-from-real-imag x y)
  (define (dispatch op)           ;; 定义名为dispatch的过程，以操作作为参数
    (cond ((eq? op 'real-part) x)
          ((eq? op 'imag-part) y)
          ((eq? op 'magnitude)
           (sqrt (+ (square x) (square y))))
          ((eq? op 'angle) (atan y x))
          (else
           (error "Unknown op -- MAKE-FROM-REAL-IMAG" op))))
  dispatch)                      ;; 把过程dispatch作为返回值

对应的apply-generic：

(define (apply-generic op arg) (arg op))

练习 2.75

用消息传递的方式实现make-from-mag-ang：

;;; 75-make-from-mag-ang.scm

(define (make-from-mag-ang x y)
    (define (dispatch op)
        (cond ((eq? op 'real-part)
                (* x (cos y)))
              ((eq? op 'imag-part)
                (* x (sin y)))
              ((eq? op 'magnitude)
                x)
              ((eq? op 'angle)
                y)
              (else
                (error "Unkonw op  -- MAKE-FROM-MAG-ANG" op))))
    dispatch)

测试：

1 ]=> (load "75-make-from-mag-ang.scm")
;Loading "75-make-from-mag-ang.scm"... done
;Value: make-from-mag-ang

1 ]=> (define c (make-from-mag-ang 3 4))    ;Value: c
1 ]=> (c 'real-part)                        ;Value: -1.960930862590836
1 ]=> (c 'imag-part)                        ;Value: -2.2704074859237844
1 ]=> (c 'magnitude)                        ;Value: 3
1 ]=> (c 'angle)                            ;Value: 4

练习 2.76 三种不同策略的可扩展性

讨论三种不同策略的可扩展性：

显式分派：这种策略在增加新操作时需要使用者避免命名冲突，而且每当增加新类型时，所有通用操作都需要做相应的改动，这种策略不具有可加性，因此无论是增加新操作还是增加新类型，这种策略都不适合。
数据导向：数据导向可以很方便地通过包机制增加新类型和新的通用操作，因此无论是增加新类型还是增加新操作，这种策略都很适合。
消息传递：消息传递将数据对象和数据对象所需的操作整合在一起，因此它可以很方便地增加新类型，但是这种策略不适合增加新操作，因为每次为某个数据对象增加新操作之后，这个数据对象已有的实例全部都要重新实例化才能使用新操作。