ch02 构造数据抽象 part05
带有通用型操作的系统
现在已经有了三套算术系统:
-
内置整数运算:
+、-、*、/ -
有理数运算:
add-rat、, sub-rat、, mul-rat、, div-rat -
复数运算:
add-complex、sub-complex、mul-complex、div-complex
现在研究如何用一套运算系统(add、sub、mul、div)把他们包含起来:
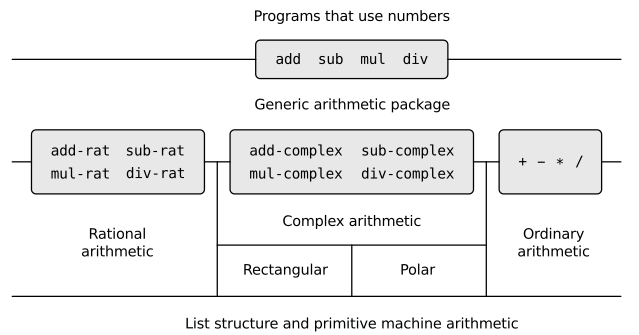
通用型自述运算
定义通用型的方法:
(define (add x y) (apply-generic 'add x y)) (define (sub x y) (apply-generic 'sub x y)) (define (mul x y) (apply-generic 'mul x y)) (define (div x y) (apply-generic 'div x y))
处理常规数的程序(语言中内置的数字类型),每个操作都有两个参数,所以用表
(scheme-number scheme-number)作为表格中的键值:
(define (install-scheme-number-package)
(define (tag x)
(attach-tag 'scheme-number x))
(put 'add '(scheme-number scheme-number)
(lambda (x y) (tag (+ x y))))
(put 'sub '(scheme-number scheme-number)
(lambda (x y) (tag (- x y))))
(put 'mul '(scheme-number scheme-number)
(lambda (x y) (tag (* x y))))
(put 'div '(scheme-number scheme-number)
(lambda (x y) (tag (/ x y))))
(put 'make 'scheme-number
(lambda (x) (tag x)))
'done)
有理数的部分可以直接使用2.1.1节的有理数代码,不用任何修改:
(define (install-rational-package)
;; internal procedures
(define (numer x) (car x))
(define (denom x) (cdr x))
(define (make-rat n d)
(let ((g (gcd n d)))
(cons (/ n g) (/ d g))))
(define (add-rat x y)
(make-rat (+ (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (numer x) (denom y))
(* (numer y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (numer x) (numer y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (numer x) (denom y))
(* (denom x) (numer y))))
;; interface to rest of the system
(define (tag x) (attach-tag 'rational x))
(put 'add '(rational rational)
(lambda (x y) (tag (add-rat x y))))
(put 'sub '(rational rational)
(lambda (x y) (tag (sub-rat x y))))
(put 'mul '(rational rational)
(lambda (x y) (tag (mul-rat x y))))
(put 'div '(rational rational)
(lambda (x y) (tag (div-rat x y))))
(put 'make 'rational
(lambda (n d) (tag (make-rat n d))))
'done)
(define (make-rational n d)
((get 'make 'rational) n d))
处理复数的部分采用标题complex,可以使用2.4.1中的过程:
(define (install-complex-package)
;; imported procedures from rectangular and polar packages
(define (make-from-real-imag x y)
((get 'make-from-real-imag 'rectangular) x y))
(define (make-from-mag-ang r a)
((get 'make-from-mag-ang 'polar) r a))
;; internal procedures
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (- (real-part z1) (real-part z2))
(- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (* (magnitude z1) (magnitude z2))
(+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (/ (magnitude z1) (magnitude z2))
(- (angle z1) (angle z2))))
;; interface to rest of the system
(define (tag z) (attach-tag 'complex z))
(put 'add '(complex complex)
(lambda (z1 z2) (tag (add-complex z1 z2))))
(put 'sub '(complex complex)
(lambda (z1 z2) (tag (sub-complex z1 z2))))
(put 'mul '(complex complex)
(lambda (z1 z2) (tag (mul-complex z1 z2))))
(put 'div '(complex complex)
(lambda (z1 z2) (tag (div-complex z1 z2))))
(put 'make-from-real-imag 'complex
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'complex
(lambda (r a) (tag (make-from-mag-ang r a))))
'done)
在复数包外用直角坐标和极坐标两种方式的构造过程:
(define (make-complex-from-real-imag x y) ((get 'make-from-real-imag 'complex) x y)) (define (make-complex-from-mag-ang r a) ((get 'make-from-mag-ang 'complex) r a))
在这里标志系统带有两层:
- 外层(complex)把这个数引入到复数包
- 内层(rectangular或polar)引入到直角坐标或是级坐标。
练习 2.77
练习 2.78
练习 2.79
练习 2.80
不同类型数据的组合
之前所有的运算,都把不同数据类型作为相互分离的东西。
更进一步让不同类型的数据操作(如一个得数和一个常规数相加)。
如果通过额外定义接受不同类型参数的过程,所有的组合太多,实现起来不实现。 (如,加法要定义:有理数和复数相加、复数和有理数相加、复数和常规数相加等等……)
强制
把一个类型强制作为另一个类型的对象。如把常规数值转换为虚部为0的复数:
(define (scheme-number->complex n) (make-complex-from-real-imag (contents n) 0))
把这些强制过程安装到一个特殊的表格中,用两个类型的名字作为索引:
(put-coercion 'scheme-number 'complex scheme-number->complex)
修改apply-generic过程,先检查是否有实际参数类型的操作,没有的话就使用强制转换
:
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(if (= (length args) 2)
(let ((type1 (car type-tags))
(type2 (cadr type-tags))
(a1 (car args))
(a2 (cadr args)))
(let ((t1->t2 (get-coercion type1 type2))
(t2->t1 (get-coercion type2 type1)))
(cond (t1->t2
(apply-generic op (t1->t2 a1) a2))
(t2->t1
(apply-generic op a1 (t2->t1 a2)))
(else
(error "No method for these types"
(list op type-tags))))))
(error "No method for these types"
(list op type-tags)))))))
使用强制要为每一对类型的转换写一个过程,但也有省力的方法,比如有A -> b和
B -> C,那可以把这两个连起来实现A -> C。进一点可以发展为一个程序自动根据
现有的转换图生成对应的转换。
还有一些情况下无法实现A与B的转换,但它们都可以转为C,那就都转为C操作。
类型的层次结构
可以在逻辑上组织类型层次:

优点:
-
这样给每个类型实现一个
raise过程实现提升到上一个层次的类型,这样可以方便地 把不同的类型转到同一个层次。 - 每个类型可以「继承」超类定义的所有操作。
- 每个类型定义一个「下降」的方法,可以转变为简单的数据结构。 比如:\(6 + 0i\)其实就是\(6\)。
层次结构的不足
如果是网状的结构就会存在多个途径来「提升」类型,为了转变为正确的类型要在网络里 时行大规模的搜索。大型系统的设计中,即要处理好相互关联的类型,又要保证模块性, 这是一个非常困难的课题。
描述不同类型之间关系的问题在哲学中称为「本体论」。而且如今有很多编程语言中使用了 并不合适的本体理论。比如面向对象的大部分理论问题就是对类型之间通用型操作的处理。 本书第三章关于局部状态的内容就回避了「类」或「继承」话题。
本书的猜想是,如果没有知识表示和自动推理工作的帮助,仅仅通过计算机语言的设计是 无法合理处理这些问题的。
练习 2.82
#lang racket
(require "getput.scm")
(define (attach-tag type-tag contents)
(if (number? contents) ;2-78
contents
(cons type-tag contents)))
(define (type-tag datum)
(cond
((number? datum) 'scheme-number) ;2-78
((pair? datum) (car datum))
(else (error "bad tagged datum -- TYPE-TAG: " datum))))
(define (contents datum)
(cond
((number? datum) datum) ;2-78
((pair? datum) (cdr datum))
(else (error "bad tagged datum -- CONTENTS: " datum))))
;; not tested
(define (coerce-all args)
(define (coerced-to type-dest remain)
(if (null? remain)
'()
(let*
((arg-src (car remain))
(type-src (type-tag arg-src)))
(if (eq? type-src type-dest)
(cons arg-src (coerced-to type-dest (cdr remain)))
(let ((coerce-func (get-coercion type-src type-dest)))
(if coerce-func
(cons (coerce-func arg-src) (coerced-to type-dest (cdr remain)))
#f))))))
(define (coerced-iter types)
(if (null? types)
#f
(let*
((type-dest (car types))
(coerced-args (coerced-to type-dest args)))
(if coerced-args
coerced-args
(coerced-iter (cdr types))))))
(coerced-iter (map type-tag args)))
(define (apply-generic op . args)
(let*
((type-tags (map type-tag args))
(proc (get op type-tags)))
(if (not (null? proc))
(apply proc (map contents args))
(let ((coerced-args (coerce-all args)))
(if coerced-args
(apply-generic op coerced-args)
(error "no available method to apply to: " (list op args)))))))
练习 2.83
#lang racket
(require "getput.scm")
(provide
make-integer
make-rational
make-real
make-complex
attach-tag
type-tag
contents
apply-generic)
(define (make-integer i)
(attach-tag 'integer i))
(define (make-rational n d)
(attach-tag 'rational (/ n d)))
(define (make-real r)
(attach-tag 'real (exact->inexact r)))
(define (make-complex r i)
(attach-tag 'complex (make-rectangular r i)))
;; don't need the 'integer special treating, so copied from apply-generic.scm
;;
(define (attach-tag type-tag contents)
(cons type-tag contents))
(define (type-tag datum)
(cond
((pair? datum) (car datum))
(else (error "bad tagged datum -- TYPE-TAG: " datum))))
(define (contents datum)
(cond
((pair? datum) (cdr datum))
(else (error "bad tagged datum -- CONTENTS: " datum))))
(define (apply-generic op . args)
(let*
((type-tags (map type-tag args))
(proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(error
"no method available for types -- APPLY-GENERIC: "
(list op type-tags)))))
#lang racket
(require "getput.scm")
(require "2-83-base.scm")
(provide
raise)
(define (install-raise-package)
(define (raise-integer i) (make-rational i 1))
(define (raise-rational r) (make-real r))
(define (raise-real r) (make-complex r 0))
(put 'raise '(integer) raise-integer)
(put 'raise '(rational) raise-rational)
(put 'raise '(real) raise-real)
'raise-package-installed)
(install-raise-package)
(define (raise i) (apply-generic 'raise i))
#|
(raise (make-integer 3))
(raise (make-rational 3 4))
(raise (make-real 0.75))
|#
练习 2.84
#lang racket
(require "getput.scm")
(require "2-83-base.scm")
(require "2-83.scm")
(provide
get-level
raise-to
apply-generic-raise
tag-op
)
(define (get-level type)
(cond
((eq? type 'integer) 1)
((eq? type 'rational) 2)
((eq? type 'real) 3)
((eq? type 'complex) 4)
(else (error "unknown type: " type))))
(define (raise-to level arg)
(if (= level (get-level (type-tag arg)))
arg
(raise-to level (raise arg))))
(define (raise-all-to level remain)
(if (null? remain)
'()
(cons
(raise-to level (car remain))
(raise-all-to level (cdr remain)))))
(define (raise-all args)
(let
((max-level
(apply
max
(map (lambda (x) (get-level (type-tag x))) args))))
(raise-all-to max-level args)))
(define (apply-generic-raise op args)
(let*
((type-tags (map type-tag args))
(proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(let*
((raised-args (raise-all args))
(proc (get op (type-tag (car raised-args)))))
;(display raised-args) (newline)
(if proc
(apply proc (map contents raised-args))
(error "no method for: " (list op args)))))))
(define (tag-op tag op)
(lambda args (attach-tag tag (apply op args))))
(define (install-add-package)
(put 'add 'integer (tag-op 'integer +))
(put 'add 'rational (tag-op 'rational +))
(put 'add 'real (tag-op 'real +))
(put 'add 'complex (tag-op 'complex +))
'install-add-ok)
(install-add-package)
(define (add . args)
(apply-generic-raise 'add args))
#|
(add
(make-integer 1)
(make-real 3.5))
(add
(make-real 3.5)
(make-integer 1))
(add
(make-integer 1)
(make-rational 1 4)
(make-real 0.75)
(make-complex 0 3))
(add
(make-complex 0 3)
(make-rational 1 4)
(make-real 0.75)
(make-integer 1))
;|#
练习 2.85
#lang racket
(require "getput.scm")
(require "2-83-base.scm")
(require "2-83.scm")
(require "2-84.scm")
(define (install-project-package)
(define (project-rational r) (make-integer (round r)))
(define (project-real r)
(let* ((rat (inexact->exact r))
(numer (numerator rat))
(denom (denominator rat)))
(make-rational numer denom)))
(define (project-complex r) (make-real (real-part r)))
(put 'project '(rational) project-rational)
(put 'project '(real) project-real)
(put 'project '(complex) project-complex)
'project-package-installed)
(install-project-package)
(define (project x)
(apply-generic 'project x))
;; project tests
;#|
(project (make-complex 3 4))
(project (project (make-complex 3 4)))
(project (project (project (make-complex 3 4))))
(project (make-real 0.75))
(project (make-rational 3 4))
(newline)
;|#
(define (near-eqv? x y)
(define (diff a b) (abs (- a b)))
(define tolerance 0.0001)
(define (f-eq? f1 f2) (< (diff f1 f2) tolerance))
(let* ((xx (contents x))
(yy (contents y)))
(and
(f-eq? (real-part xx) (real-part yy))
(f-eq? (imag-part xx) (imag-part yy)))))
(define (drop x)
;(display "drop: ") (display x) (newline)
(if (eq? 'integer (type-tag x))
x
(let*
((projected (project x))
(raised (raise projected)))
;(display "drop: ") (display projected) (display raised) (newline)
; equal? is not enought since the inexact comparison
(if (near-eqv? raised x)
(drop projected)
x))))
;; drop tests
(drop (make-complex 3.0 4.0))
(drop (make-complex 3.5 0.0))
(drop (make-complex 3/2 0.0))
(drop (make-complex 3.0 0.0))
(newline)
;; it's non-trivial to deal with multiple return value,
;; so just make yourself believe it returns only one number ...
(define (apply-generic-raise-drop1 op args)
(let ((ans (apply-generic-raise op args)))
(drop ans)))
(define (add . args)
(apply-generic-raise-drop1 'add args))
;; tests
;#|
(add
(make-integer 1)
(make-real 3.5))
(add
(make-real 3.5)
(make-integer 1))
(add
(make-integer 1)
(make-rational 1 4)
(make-real 0.75)
(make-complex 0 3)
(make-complex 0 -3.0))
(add
(make-complex 0.5 -3.0)
(make-complex 0 3)
(make-rational 1 4)
(make-real 0.75)
(make-integer 1))
;|#
练习 2.86
实例:符号代数
练习 2.87
#lang racket
(require "getput.scm")
(require "apply-generic.scm")
(require "generic-op.scm")
(require "2.5.3-poly.scm")
(require "2.5.3-term.scm")
(require "2-80.scm")
(define (install-zero-poly?)
(define (zero-poly? terms)
;(display "zero?: ") (display terms) (newline)
(cond
((null? terms) #t)
((=zero? (coeff (first-term terms)))
(zero-poly? (rest-terms terms)))
(else #f)))
(put '=zero? '(polynomial) (lambda (poly) (zero-poly? (contents (term-list poly)))))
'zero-poly-installed)
(install-zero-poly?)
#|
(=zero? '(polynomial x termlist (1 0) (0 1)))
(=zero? '(polynomial x termlist (1 0) (0 0)))
(=zero? '(polynomial x termlist (1 1) (0 0)))
(=zero? '(polynomial x termlist))
(=zero? '(polynomial x termlist (2 (polynomial y termlist (1 1) (0 1))) (1 0) (0 1)))
(=zero? '(polynomial x termlist (2 (polynomial y termlist (1 0) (0 1))) (1 0) (0 1)))
(=zero? '(polynomial x termlist (2 (polynomial y termlist (1 0) (0 0))) (1 0) (0 0)))
|#
(define poly1
'(polynomial x termlist
(5 4)
(3 (polynomial y termlist (1 -1) (0 -1)))
(2 (polynomial y termlist (1 1) (0 1)))
(1 (polynomial y termlist (1 1) (0 1)))
(0 3)))
(define poly2
'(polynomial x termlist
(4 3)
(3 (polynomial y termlist (1 1) (0 1)))
(1 (polynomial y termlist (1 2) (0 -1)))
(0 2)))
poly1
poly2
(add poly1 poly2)