ch03 模块化、对象和状态 part01
赋值和局部状态
用一个或几个状态变量刻画一个对象的状态。为了描述实际对象的状态,每一个对象必须 有它自己的一些局部状态变量。
局部状态变量
之前章节中的过程都是数学函数描述,对一个过程的调用将计算出相应函数作用于指定 参数所得到的值。在这样的情况下,同样的参数多次调用同一个过程总会产生出 相同的结果。
另一种情况是带有状态变化的程序,比如银行取款程序要涉及到状态的变化。 但如果程序中涉及了状态变量和赋值,那么之前介绍的代换模型就不适合再作为过程应用 的模型了。3.2节会会介绍新的模型。
赋值操作set!
Scheme中的特殊形式set!改变变量值:
(set! <name> <new-value>)
Scheme约定用!结尾的命名表示改变值的操作。
表达式序列begin
特殊形式begin用于对多个表达式求值。
(begin <exp1> <exp2> ... <expk>)
每个表达式会依次求值,最后一个表达式<expk>的值会作为整个begin表达式的值
返回。
Schem里的过程本身就可以是表达式序列。另外cond表达式中的<consequent>部分
不仅可以是表达式,也可以是表达式序列。
模拟银行取款程序
定义balance作为余额,withdraw作为取款的过程:
(define balance 100)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
重构,把withdraw和balance作为内部成员:
(define new-withdraw
(let ((balance 100))
(lambda (amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))))
再重构,以余额为参数,成为类似工厂方法的模式返回lambda表达式:
(define (make-withdraw balance)
(lambda (amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds")))
可以用来构建两个账记实例:
(define W1 (make-withdraw 100)) (define W2 (make-withdraw 100)) (W1 50) ;; 50 (W2 70) ;; 30 (W2 40) ;; "Insufficient funds" (W1 40) ;; 10
增加存款功能:
(define (make-account balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
(else (error "Unknown request -- MAKE-ACCOUNT"
m))))
dispatch) ;; return dispatch method
使用指定的参数'withdraw或'deposit指定是存款还是取款,属于「消息传递风格」:
(define acc (make-account 100)) ((acc 'withdraw) 50) ;; 50 ((acc 'withdraw) 60) ;; "Insufficient funds" ((acc 'deposit) 40) ;; 90 ((acc 'withdraw) 60) ;; 30
还可能创建另外一个账户实例:
(define acc2 (make-account 100))
练习 3.1 :实现累加器工厂
定义:
;;; 1-make-accumulator.scm
(define (make-accumulator value)
(lambda (add-value)
(set! value (+ value add-value))
value))
需要说明的一点是,因为在 lambda 体内有一个隐式的begin,所以可以直接在lambda
里面使用多条表达式。
测试:
1 ]=> (load "1-make-accumulator.scm") ;Loading "1-make-accumulator.scm"... done ;Value: make-accumulator 1 ]=> (define A (make-accumulator 5)) ;Value: a 1 ]=> (A 10) ;Value: 15 1 ]=> (A 10) ;Value: 25
练习 3.2 :统计调用次数
过程make-monitored过程以过程f作为参数,返回另一个过程mf。mf内部有一个
计数器统计记录自己被调用的次数,它的功能包括:
-
如果
mf收到一个特殊的实参符号how-many-calls?时,返回调用的次数。 -
如果
mf收到特殊的实参符号reset-count则重置读数器。 -
其他的实参,
mf调用f,并把f的结果返回。
所以make-monitored要完成四件事:
-
包装起输入的函数
f以及一个计数局部变量count-call -
检查被包装函数的输入,当输入为
'how-many-calls?时,返回count-call的值 -
检查被包装函数的输入,当输入为
'reset-count时,将count-call的值重置为0。 -
如果输入既不是
'how-many-calls,也不是'reset-count,那么将count-call的 数值加一,并使用输入调用函数f
;;; 2-make-monitored.scm
(define (make-monitored f)
(let ((count-call 0))
(lambda (input)
(cond ((eq? input 'how-many-calls?)
count-call)
((eq? input 'reset-count)
(begin (set! count-call 0)
count-call))
(else (begin (set! count-call (+ 1 count-call))
(f input)))))))
测试:
1 ]=> (load "2-make-monitored.scm") ;Loading "2-make-monitored.scm"... done ;Value: make-monitored 1 ]=> (define s (make-monitored sqrt)) ;Value: s 1 ]=> (s 100) ;Value: 10 1 ]=> (s 'how-many-calls?) ;Value: 1 1 ]=> (s 9) ;Value: 3 1 ]=> (s 99) ;Value: 9.9498743710662 1 ]=> (s 'how-many-calls?) ;Value: 3 1 ]=> (s 'reset-count) ;Value: 0 1 ]=> (s 'how-many-calls?) ;Value: 0
练习 3.3:带密码的取款程序
以下是带密码验证功能的 make-account 函数的定义:
;;; 3-make-account.scm
(define (make-account blance password)
(define (withdraw amount)
(if (>= blance amount)
(begin (set! blance (- blance amount))
blance)
"Insufficient funds"))
(define (deposit amount)
(set! blance (+ blance amount)))
(define (password-match? given-password) ; 新增
(eq? given-password password)) ;
(define (display-wrong-password-message useless-arg) ; 新增
(display "Incorrect password")) ;
(define (dispatch given-password mode)
(if (password-match? given-password) ; 新增
(cond ((eq? mode 'withdraw)
withdraw)
((eq? mode 'deposit)
deposit)
(else
(error "Unknow request -- MAKE-ACCOUNT" mode)))
display-wrong-password-message)) ; 新增
dispatch)
display-wrong-password-message的定义和调用方式有点奇怪,主要是因为dispatch
要求我们必须返回一个接受单个参数的函数(否则解释器会报错),所以为了兼容性考虑,
display-wrong-password-message接受一个不会用到的参数,并且作为dispatch的
其中一个分派函数。
测试:
1 ]=> (load "3-make-account.scm") ;Loading "3-make-account.scm"... done ;Value: make-account 1 ]=> (define acc (make-account 100 'secret-password)) ;Value: acc 1 ]=> ((acc 'secret-password 'withdraw) 40) ;Value: 60 1 ]=> ((acc 'some-other-password 'deposit) 60) Incorrect password ;Unspecified return value
练习 3.4:限制输入密码错误次数
如果连接输入密码错误7次,会报警(调用call-the-cops)。
;;; 4-make-account.scm
(define (make-account blance password)
(let ((max-try-times 7)
(try-times 0))
(define (withdraw amount)
(if (>= blance amount)
(begin (set! blance (- blance amount))
blance)
"Insufficient funds"))
(define (deposit amount)
(set! blance (+ blance amount)))
(define (password-match? given-password)
(eq? given-password password))
(define (display-wrong-password-message useless-arg)
(display "Incorrect password"))
(define (dispatch given-password mode)
(if (password-match? given-password)
(begin
(set! try-times 0) ; 成功登录之后清零计数器
(cond ((eq? mode 'withdraw)
withdraw)
((eq? mode 'deposit)
deposit)
(else
(error "Unknow request -- MAKE-ACCOUNT" mode))))
(begin
(set! try-times (+ 1 try-times)) ; 进行计数
(if (>= try-times max-try-times)
(call-the-cops)
display-wrong-password-message))))
dispatch))
(define (call-the-cops)
(error "You try too much times, calling the cops ..."))
测试:
1 ]=> (load "4-make-account.scm") ;Loading "4-make-account.scm"... done ;Value: call-the-cops 1 ]=> (define acc (make-account 100 'secret-password)) ;Value: acc 1 ]=> ((acc 'wrong-password 'withdraw) 50) Incorrect password ;Unspecified return value 1 ]=> ((acc 'wrong-password 'withdraw) 50) Incorrect password ;Unspecified return value 1 ]=> ((acc 'wrong-password 'withdraw) 50) Incorrect password ;Unspecified return value 1 ]=> ((acc 'wrong-password 'withdraw) 50) Incorrect password ;Unspecified return value 1 ]=> ((acc 'wrong-password 'withdraw) 50) Incorrect password ;Unspecified return value 1 ]=> ((acc 'wrong-password 'withdraw) 50) Incorrect password ;Unspecified return value 1 ]=> ((acc 'wrong-password 'withdraw) 50) ;You try too much times, calling the cops ... ;To continue, call RESTART with an option number: ; (RESTART 1) => Return to read-eval-print level 1.
引进赋值带来的利益
有了赋值以后,就不用把当前状态作为下一次调用时的参数传来传去了。在需要让计算对象 的行为随着时间变化的场景下,用局部状态变量去模拟系统的状态,用对这些变量的赋值 去模拟状态的变化。
练习 3.5:蒙特卡罗积分
蒙地卡羅法(Monte Carlo Method)求圓周率的原理示意圖如下。
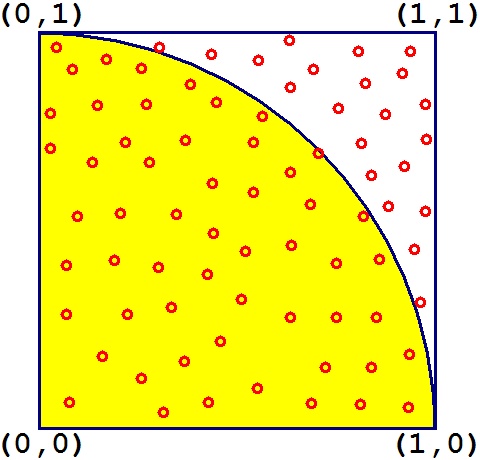
正方形邊長為1單位長,面積為1平方單位;黃色扇形面積等於半徑為1單位長的 \(\frac{1}{4}\)圓,面積為\(\frac{pi}{4}\)。在正方形內均勻隨機丟石頭:
\[ \begin{equation} \begin{split} \text{落在扇型內的機率} = \frac{扇型面積}{正方形面積} = \frac{\pi}{4} \end{split} \end{equation} \]所以只要隨機產生\(N\)個座標\((x,y)\),看看座標\((x,y)\)落在扇形中(\(x^2+y^2<1\))的次數 有幾次。落在扇形中的次數除以N再乘上4的數值理論上就會接近圓周率PI。
程式中我們要不斷產生\(0 \leq x, y \lt 1\)的座標點。
以下是相应的定义:
;;; 5-estimate-integral.scm
(load "p155-monte-carlo.scm")
(load "5-random-in-range.scm")
(define (estimate-integral p? x1 x2 y1 y2 trials)
(* 4
(monte-carlo trials
(lambda ()
(p? (random-in-range x1 x2)
(random-in-range y1 y2))))))
(define (get-pi trials)
(exact->inexact
(estimate-integral (lambda (x y)
(< (+ (square x)
(square y))
1.0))
-1.0
1.0
-1.0
1.0
trials)))
另外需要一提的是, scheme 的random函数的作用是,当传给它一个浮点数时,
它产生的是浮点随机数,如果传给它一个整数,它产生的就是整数随机数:
1 ]=> (random 5) ;Value: 3 1 ]=> (random 5.0) ;Value: 3.533225811316893
因为这道练习要求随机函数产生浮点类型的随机值,所以练习给出的random-in-range
也要做出相应的修改:
;;; 5-random-in-range.scm
(define (random-in-range low high)
(let ((range (- high low)))
(+ low
(random (exact->inexact range))))) ; 确保生成浮点随机数
书本 155 页的monte-carlo直接敲下来:
测试:
1 ]=> (load "5-estimate-integral.scm") ;Loading "5-estimate-integral.scm"... ; Loading "p155-monte-carlo.scm"... done ; Loading "5-random-in-range.scm"... done ;... done ;Value: get-pi 1 ]=> (get-pi 1000) ;Value: 3.176 1 ]=> (get-pi 10000) ;Value: 3.1468 1 ]=> (get-pi 10000000) ;Value: 3.14181
练习 3.6:可重置的随机数生成器
-
(rand 'generate)生成新随机数。 -
((rand 'reset) <new-value>)设置内部状态为<new-value>。这样可以生成重复的 随机数序列。
#lang racket (define rand (let ((x 0) (update (lambda (x) (remainder (+ 65537 (* x 1027)) 1048577)))) (lambda (op) (cond ((eq? op 'generate) (set! x (update x)) x) ((eq? op 'reset) (lambda (new-value) (set! x new-value))) (else (error "unknown operation")))))) (rand 'generate) (rand 'generate) (rand 'generate) (newline) ((rand 'reset) 0) (rand 'generate) (rand 'generate) (rand 'generate)
引进赋值的代价
函数式程序设计:不使用赋值,相同的参数就一定会产生出相同的结果。
使用了赋值,就不能使用数学性质的模型。因为代换的基础是把符号作为值的名字, 但赋值操作会改变符号的值,所以符号不能再代表值的名字。
比如不考虑余额验证的简化版的取款操作: 如果不使用赋值,那返回的就是一个操作减法的lambda,不会保存变化过程:
(define (make-decrementer balance)
(lambda (amount)
(- balance amount)))
(define D (make-decrementer 25))
(D 20) ; 5
(D 10) ; 15
可以使用代换模型来解释执行过程:
((make-decrementer 25) 20) ((lambda (amount) (- 25 amount)) 20) (- 25 20) ; result is 5
如果引入了赋值操作:
(define (make-simplified-withdraw balance)
(lambda (amount)
(set! balance (- balance amount))
balance))
(define W (make-simplified-withdraw 25))
(W 20) ; 5
(W 10) ; - 5
如果用代换过程来解释它,:
((make-simplified-withdraw 25) 20) ;; 用实参25来代替形参balance ((lambda (amount) (set! balance (- 25 amount)) 25) 20) ;; 用20来代换lambda里的amount (set! balance (- 25 20)) 25
到了这一步,如果硬套代换模型的话,就表示要把balance设置为5,然后把25作为
返回值。这显然是错误的。
因为赋值操作会改变符号的值,所以set!操作前后的两个balance的值不相同,
需要作为两个不同的对象区分。
代换模型里是不能这样做的,代换模型中符号就是值的表示。
同一和变化
如果语言支持同一性,这个语言就称为是具有「引用透明性」。
同一性表示两个对象在任何表达式里都可以相互替换,而不会改变表达式的求值结果。
比如前面定义的make-decrementer纯函数的过程:
(define D1 (make-decrementer 25)) (define D2 (make-decrementer 25))
相反就是变化性,比如前面定义的带赋值的make-simplified-withdraw:
(define W1 (make-simplified-withdraw 25)) (define W2 (make-simplified-withdraw 25)) (W1 20) ; 5 (W1 20) ; - 15 (W2 20) ; 5
同一性问题的例子,以下两个场景有着本质的区别:
不同的对象的场景,下,改变了一个,另一个不会变:
(define peter-acc (make-account 100)) (define paul-acc (make-account 100))
同一个对象的场景,改变了一个,另一个也会变:
(define peter-acc (make-account 100)) (define paul-acc peter-acc)
所以如果没有赋值操作,就可以简化同一性问题,因为只要值一样,就不会再变, 可以作为同一个对象对待。
命令式程序设计的缺陷
「命令式程序设计」:与「函数式程序设计」相对的,广泛采用赋值操作的程序。
命令式程序设计强迫人们为了保证每个语句所修改是正确的版本而考虑赋值的顺序。
比如函数式求阶乘程序:
(define (factorial n)
(define (iter product counter)
(if (> counter n)
product
(iter (* counter product)
(+ counter 1))))
(iter 1 1))
如果改为命令式的阶乘程序:
(define (factorial n)
(let ((product 1)
(counter 1))
(define (iter)
(if (> counter n)
product
(begin (set! product (* counter product))
(set! counter (+ counter 1))
(iter))))
(iter)))
就不能搞错赋值顺序,比如反一下以下两句,结果就错了:
(set! counter (+ counter 1)) (set! product (* counter product))
在并发环境下,复杂性还会更加高。
练习 3.7
定义创建账号的过程make-joint,它有三个参数:
- 账号(要存在)
- 密码(要和老密码一样)
- 新密码
这样做的目的是创建另外一个访问已经有账号的账号。比如已经有一个账号是peter-acc
,它的密码是open-sesame,那为可以再创建一个账号pual-acc和密码rosebud
来访问它:
(define paul-acc (make-joint peter-acc 'open-sesame 'rosebud))
make-joint是对make-account所产生的对象的一次再包装。
注意因为兼容性的问题,display-wrong-another-password接受了一个不会用到的参数。
;;; 7-make-joint.scm
(define (make-joint origin-acc origin-password another-password)
(lambda (given-password mode)
(if (eq? given-password another-password)
(origin-acc origin-password mode)
display-wrong-another-password-message)))
(define (display-wrong-another-password-message useless-arg)
(display "Incorrect another password"))
测试:
1 ]=> (load "7-make-joint.scm") ;Loading "7-make-joint.scm"... done ;Value: display-wrong-another-password-message 1 ]=> (load "3-make-account.scm") ;Loading "3-make-account.scm"... done ;Value: make-account 1 ]=> (define jack-acc (make-account 100 'jack-password)) ;Value: jack-acc 1 ]=> (define peter-acc (make-joint jack-acc 'jack-password 'peter-password)) ;Value: peter-acc 1 ]=> ((peter-acc 'peter-password 'withdraw) 50) ;Value: 50 1 ]=> ((jack-acc 'jack-password 'withdraw) 0) ;Value: 50
练习 3.8:参数的求值顺序
函数式程序不用关心子表达式的求值顺序,比如多个参数是从左到右求值还是从右到左。 但是引入的赋值以后求值顺序就会影响结果。
请设计一个过程f,使得(+ (f 0) (f 1)):
-
参数在从左到右求值时返回
0 -
参数在从右到左求值时返回
1
方法有无数种,以下是其中一种比较简短的定义:
;;; 8-f.scm
(define f
(lambda (first-value)
(set! f (lambda (second-value) 0))
first-value))
f在第一次被调用的时候,返回调用它的参数first-value,然后将f设置为一个
无论接受什么参数都只返回0的过程,因此最终求值结果就由第一次调用f的参数
决定了。
测试:
1 ]=> (load "8-f.scm") ;Loading "8-f.scm"... done ;Value: f 1 ]=> (+ (f 0) (f 1)) ;Value: 1 1 ]=> (+ (f 1) (f 0)) ;Value: 0
可以看出,测试所使用的 mit-scheme 解释器对参数的求值顺序是从右到左。