ch03 模块化、对象和状态 part03

用变动数据做模拟

第二章介绍了如何实现复合数据，包括「构造函数」和「选择函数」； 这里继续研究如何创建可修改的复合数据，引入了「改变函数」。

变动表结构

增加对序对的修改操作。

定义修改序对的第一个指针：

(set-car! <rec> <new-car>)

定义修改序对的第二个指针：

(set-cdr! <rec> <new-cdr>)

用set-car!和set-cdr!来重新定义cons操作：

(define (cons x y)
  (let ((new (get-new-pair)))   ;; 拿一个序对来，然后修改两个指针的指向
    (set-car! new x)
    (set-cdr! new y)
    new))

练习3.12

连接两个列表可以有两种实现，一种不是修改原来有表的，返回新表作为结果：

(define (append x y)
  (if (null? x)
      y
      (cons (car x) (append (cdr x) y))))

还有一种直接修改x表的实现方式：

(define (append! x y)
  (set-cdr! (last-pair x) y)    ;; 把y接到x的最后一个元素后面
  x)

;; 取最后一个元素的过程
(define (last-pair x)
  (if (null? (cdr x))
      x
      (last-pair (cdr x))))

填写以下操作的输出：

1 ]=> (define x (list 'a 'b))  ;Value: x
1 ]=> (define y (list 'c 'd))  ;Value: y
1 ]=> (define z (append x y))  ;Value: z 这个是构造函数（没有 ``!`` ） 
1 ]=> z                        ;Value 12: (a b c d)
1 ]=> (cdr x)                  ;Value 13: (b)
1 ]=> (define w (append! x y)) ;Value: w ; 这个是修改函数
1 ]=> (cdr x)                  ;Value 13: (b c d)

练习3.13

(define (make-cycle x)
  (set-cdr! (last-pair x) x)
  x)

(define z (make-cycle (list 'a 'b 'c)))

求z的盒子模型与(last-pair z)的结果：

1 ]=> z           ;; a b c a b c a b c a b c a b c ;...

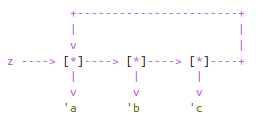
练习3.14

研究以下过程的功能是什么：

(define (mystery x)
  (define (loop x y)
    (if (null? x)
        y
        (let ((temp (cdr x)))
          (set-cdr! x y)
          (loop temp x))))
  (loop x '()))

实际上，mystery就是一个修改版的reverse函数：

1 ]=> (define v (list 'a 'b 'c)) ;Value: v 
1 ]=> (define w (mystery v))     ;Value: w 
1 ]=> w                          ;Value 11: (c b a) 
1 ]=> v                          ;Value 12: (a)

求v的盒子模型：

(define v (list 'a 'b 'c 'd))

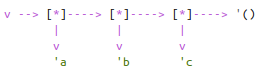
以下是执行(mystery v)的过程：

(mystery v)

(mystery (list 'a 'b 'c))

(loop (list 'a 'b 'c) '())

(let ((temp (list 'b 'c)))
    (set-cdr! (list 'a 'b 'c) '())
    (loop (list 'b 'c) (list a)))

(loop (list 'b 'c) (list a))

(let ((temp (list 'c)))
    (set-cdr! (list 'b 'c) (list a))
    (loop (list 'c) (list 'b 'a)))

(loop (list 'c) (list 'b 'a))

(let ((temp '()))
    (set-cdr! (list 'c) (list 'b 'a))
    (loop '() (list 'c 'b 'a)))

(loop '() (list 'c 'b 'a))

(list 'c 'b 'a)

以下是执行(define w (mystery v))之后w和v的盒子图形：

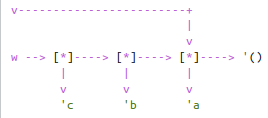
共享与相等

「共享」即表示二者是否为同一个对象，通过谓词eq?判断：

(eq? x y)

练习 3.15

练习 3.16

以下过程统计表中序对个数，实现方法是car部分加上cdr部分再加1。 这个过程错在哪里？

(define (count-pairs x)
  (if (not (pair? x))
      0
      (+ (count-pairs (car x))
         (count-pairs (cdr x))
         1)))

事实上，我们可以将序对之间的连接看作是有向图，比如(cons 1 (cons 2 '()))。

而这个count-pairs的问题是，当图中的点（也即是序对）有多于一个入度的时候， 它的计算方式就不对了。

练习 3.17 memq检查序对是否存在于表内

把count-pairs修改正确。

可以使用eq?判断对象的唯一性。我们可以通过维持一个记录列表，然后遍历给定的 序对结构，每当遇到一个序对时，判断它是否已经存在于记录列表，如果不存在就将它 加进记录列表，并继续遍历这个序对的car和cdr部分，当给定的序对结构遍历完之后， 记录列表的长度就是序对的真正个数。

memq是scheme内置过程，用来检查序对是否存在于记录表内。

;;; 17-count-pairs.scm

(define (count-pairs x)
    (length (inner x '())))

(define (inner x memo-list)
    (if (and (pair? x)
             (false? (memq x memo-list)))
        (inner (car x)
               (inner (cdr x)
                      (cons x memo-list)))
        memo-list))

memq 的手册： http://www.gnu.org/software/mit-scheme/documentation/mit-scheme-ref/Searching-Lists.html#Searching-Lists

讨论： 你这个少情况了，cycle怎么办？我觉得这个才对：

(define (count-pairs x)
  ;;; list 可以现状一个 x 进去
  (define (in? s list)
    (if (null? (cdr list))
      (eq? s (car list))
      (if (eq? s (car list))
        #t
        (in? s (cdr list)))))
  (define (iter-count l list)
    (if (null? l)
      list
      (cond ((and (not (in? (car l) list)) 
                  (not (eq? (cdr l) x))
                  (pair? (car l))) 
              (iter-count (cdr l) (append list (car l))))
        ((eq? (cdr l) x) "Maximum. It is Cycle")
        (else (iter-count (cdr l) list)))))
  (iter-count x (list x)))

练习 3.18：检查环型结构

检查表中是否有包含环形结构（不断cdr会陷入无穷循环）。可以采用以下方式：

• 设置一个唯一的标识符identity(可以用cons配合eq?来做到这一点)
• 遍历列表，使用eq?检查列表的每个序对的car部分是否和identity相等， 如果相等的话，那么这个列表有环，如果不相等，那么将这个序对的car部分设置为 identity，然后继续遍历列表的cdr部分，直到发现环或者列表为空为止。

以下是过程的定义：

;;; 18-loop.scm
(define (loop? lst)
    (let ((identity (cons '() '())))
        (define (iter remain-list)
            (cond ((null? remain-list)
                    #f)
                  ((eq? identity (car remain-list))
                    #t)
                  (else
                    (set-car! remain-list identity)
                    (iter (cdr remain-list)))))
        (iter lst)))

1 ]=> (loop? (list 1 2 3))                           ;Value: #f 
1 ]=> (define loop (list 1 2 3))                     ;Value: loop 
1 ]=> (set-cdr! (last-pair loop) loop)               ;Unspecified return value 
1 ]=> (loop? loop)                                   ;Value: #t 
1 ]=> (define loop-list (list 1 2 3))                ;Value: loop-list 
1 ]=> (set-cdr! (last-pair loop-list) loop-list)     ;Unspecified return value 
1 ]=> (loop? loop-list)                              ;Value: #t 

讨论：破坏了原来的列表的确不太好。另外这个问题的最直接的想法应该是用一个列表来 纪录所有遇到过的序对，然后每次检查一个新的序对时，查找是否它已经出现在序对中。 因为此算法空间按n增长，所以下一题很自然地要我们实现常量空间的算法。

练习 3.19

用空间常量的算法来实现上一问题。

使用常量空间判断列表是否有环的算法可以很容易地在网络上找到， 算法的核心思想是这样的：

• 使用两个变量，一个变量以步长为1遍历列表，另一个变量以步长为2遍历列表， 每次在两个变量移动之后对比它们，如果两个变量相遇，那么列表有环；
• 如果能走完整个列表（遇到'()），那么列表没有环。

以下是这一算法相应的过程定义：

(define (loop? lst)
    (define (iter x y)
        (let ((x-walk (list-walk 1 x))
              (y-walk (list-walk 2 y)))
            (cond ((or (null? x-walk) (null? y-walk))
                    #f)
                  ((eq? x-walk y-walk)
                    #t)
                  (else
                    (iter x-walk y-walk)))))
    (iter lst lst))

(define (list-walk step lst)
    (cond ((null? lst)
            '())
          ((= step 0)
            lst)
          (else
            (list-walk (- step 1)
                       (cdr lst)))))

(loop? (list 1 2 3))                               ;Value: #f 

(define circular-list (list 1 2 3))                ;Value: circular-list 

(set-cdr! (last-pair circular-list) circular-list) ;Unspecified return value 

(loop? circular-list)                              ;Value: #t

改变也是赋值

数据结构可以纯粹通过过程来实现。

比如之前已经介绍过序对的构造函数和选择函数：

(define (cons x y)
  (define (dispatch m)
    (cond ((eq? m 'car) x)
          ((eq? m 'cdr) y)
          (else (error "Undefined operation -- CONS" m))))
  dispatch)

(define (car z) (z 'car))

(define (cdr z) (z 'cdr))

可修改的数据结构也可能用过程来实现：

(define (cons x y)
  (define (set-x! v) (set! x v))
  (define (set-y! v) (set! y v))
  (define (dispatch m)
    (cond ((eq? m 'car) x)
          ((eq? m 'cdr) y)
          ((eq? m 'set-car!) set-x!)
          ((eq? m 'set-cdr!) set-y!)
          (else (error "Undefined operation -- CONS" m))))
  dispatch)
 
(define (car z) (z 'car))

(define (cdr z) (z 'cdr))

(define (set-car! z new-value)
  ((z 'set-car!) new-value)
  z)

(define (set-cdr! z new-value)
  ((z 'set-cdr!) new-value)
  z)

• 包括赋值在内的「可变对象的行为」都表现为对数据的改变。
• 赋值在模型中表现为对环境的修改，所以赋值也是改变操作。

练习 3.20

画出求值环境：

(define x (cons 1 2))
(define z (cons x x))
(set-car! (cdr z) 17)
(car x)
17

按照之前分析的习惯，先将 179 页的几个程序全部转成 lambda 表达式的形式：

以下是执行定义(define x (cons 1 2))之后的环境图：

以下是执行定义(define z (cons x x))之后的环境图：

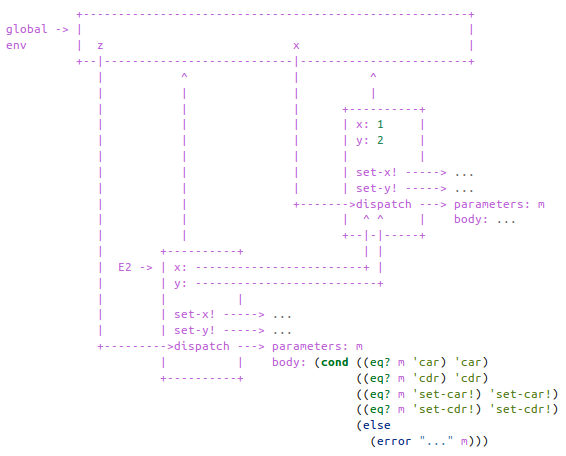
执行表达式(set-car! (cdr z) 17)有以下两个步骤：

1. 执行(cdr z)，返回x。
2. 执行(set-car! x 17)，引发表达式((x 'set-car!) 17)的执行, 然后又引发(set-x! 17)的执行。

最终，x的car部分的值被设置为17。

以下是相应的环境图：

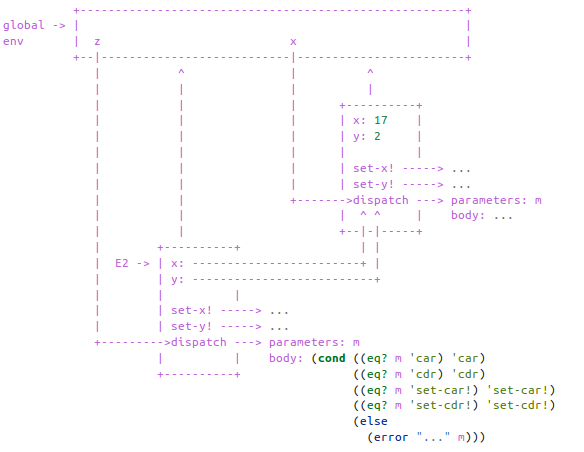
整个求值过程如下：

1 ]=> (define x (cons 1 2)) ;Value: x 
1 ]=> (define z (cons x x)) ;Value: z 
1 ]=> (set-car! (cdr z) 17) ;Value: 1 ; 使用 set! 设置变量时会返回变量的旧值 
1 ]=> (car x)               ;Value: 17 

队列的表示

增加了修改操作（set-car!、set-cdr!）以后，就可以创建新的数据结构，比如队列。

(make-queue)                           ;; 构造方法
(empty-queue?  <queue>)                ;; 是否为空
(front-queue   <queue>)                ;; 返回么一个对象（并不出队），为空报错
(insert-queue! <queue> <item>)         ;; 入队 
(delete-queue! <queue>)                ;; 出队，为空报错

入队操作要先找到队尾，遍历需要\(\Theta(n)\)。如果维护队尾指针的话，就可以简化为 \(\Theta(1)\)步。所以在这里增加：

• front-ptr指向第一个序对。
• rear-ptr指向最后一个序对。

把这两个指针cons起来，作为队列本身：

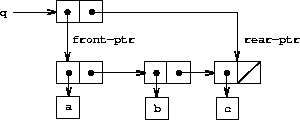
实现：

(define (front-ptr queue) (car queue))

(define (rear-ptr queue) (cdr queue))

(define (set-front-ptr! queue item) (set-car! queue item))

(define (set-rear-ptr! queue item) (set-cdr! queue item))

(define (make-queue) (cons '() '()))                    ;; 构造函数

(define (empty-queue? queue) (null? (front-ptr queue))) ;; 检查为空

;; 得到前端数据：取第一个序对的car
(define (front-queue queue)
  (if (empty-queue? queue)
      (error "FRONT called with an empty queue" queue)
      (car (front-ptr queue))))

入队操作：

1. 新建序对：car为数据，cdr为空。
2. 如果队列为空，队列前指针指向新序对。
3. 如果队列汪空，最后一个序队和队列后指针指向新序对。

(define (insert-queue! queue item)
  (let ((new-pair (cons item '())))
    (cond ((empty-queue? queue)
           (set-front-ptr! queue new-pair)
           (set-rear-ptr! queue new-pair)
           queue)
          (else
           (set-cdr! (rear-ptr queue) new-pair)
           (set-rear-ptr! queue new-pair)
           queue)))) 

出队操作只要把队列的前指针指向第二个就可以了。当队列中只有最后一个数据时， 删除后前指针变为空表。不用管后指针，empty-queue?只看前指针。

(define (delete-queue! queue)
  (cond ((empty-queue? queue)
         (error "DELETE! called with an empty queue" queue))
        (else
         (set-front-ptr! queue (cdr (front-ptr queue)))
         queue))) 

练习 3.21 队列的显示

Scheme的标准输出不能很好地显示队列，比如：

(define q1 (make-queue))
(insert-queue! q1 'a)        ;; ((a) a)
(insert-queue! q1 'b)        ;; ((a b) b)
(delete-queue! q1)           ;; ((b) b)
(delete-queue! q1)           ;; (() b)

请定义一个显示队列内容的过程：

当解释器打印出((a b) b)的时候，实际上是将q1变量的car和cdr部分都 打印了出来，这不仅暴露了队列的底层实现，而且还会让人造成误会。

要解决这个问题，我们可以使用一个只返回队列car部分的过程来作为打印队列中的值：

;;; 21-print-queue.scm

(define (print-queue queue)
    (car queue))

1 ]=> (define q1 (make-queue)) ;Value: q1 
1 ]=> (print-queue   q1)       ;Value: () 
1 ]=> (insert-queue! q1 'a)    ;Value 13: ((a) a) 
1 ]=> (print-queue   q1)       ;Value 14: (a) 
1 ]=> (insert-queue! q1 'b)    ;Value 13: ((a b) b) 
1 ]=> (print-queue   q1)       ;Value 14: (a b) 
1 ]=> (delete-queue! q1)       ;Value 13: ((b) b) 
1 ]=> (print-queue   q1)       ;Value 15: (b) 
1 ]=> (delete-queue! q1)       ;Value 13: (() b) 
1 ]=> (print-queue   q1)       ;Value: ()

实际上，打印是由解释器完成的，print-queue只是负责将队列中合适的部分返回给 解释器而已。

练习 3.22

除了用一对指针以外，还可以把队列构造为带有局部状态的过程。这里的局部状态由指向 一个常规表的开始和结束指针组成，形式为：

(define (make-queue)
  (let ((front-ptr ...)
        (rear-ptr ...))
    <definitions of internal procedures>
    (define (dispatch m) ...)
    dispatch))

完成以上实现：

实现使用了两个变量作为指针，分别指向队列的前端和后端。

(define (make-queue)
    (let ((front-ptr '())
          (rear-ptr '()))
        (define (insert-queue! item)
            (cond ((empty-queue?)
                    (let ((init-list (list item)))
                        (set! front-ptr init-list)
                        (set! rear-ptr init-list)
                        front-ptr))
                  (else
                    (let ((new-item (list item)))
                        (set-cdr! rear-ptr new-item)
                        (set! rear-ptr new-item)
                        front-ptr))))
        (define (delete-queue!)
            (cond ((empty-queue?)
                    (error "DELETE! called with an empty queue" queue))
                  (else
                    (set! front-ptr (cdr front-ptr))
                    front-ptr)))
        (define (empty-queue?)
            (null? front-ptr))
        (define (dispatch m)
            (cond ((eq? m 'insert-queue!)
                    insert-queue!)
                  ((eq? m 'delete-queue!)
                    (delete-queue!))
                  ((eq? m 'empty-queue?)
                    (empty-queue?))
                  (else
                    (error "Unknow operation -- DISPATCH" m))))
        dispatch))

1 ]=> (define q (make-queue))                   ; 创建队列 ;Value: q 
1 ]=> ((q 'insert-queue!) 'a)                   ; 插入 ;Value 11: (a) 
1 ]=> ((q 'insert-queue!) 'b)                   ;Value 11: (a b) 
1 ]=> (q 'delete-queue!)                        ; 删除 ;Value 12: (b) 
1 ]=> (q 'delete-queue!)                        ;Value: () 
1 ]=> (q 'empty-queue?)                         ; 空队列 ;Value: #t 
1 ]=> ((q 'insert-queue!) 'not-empty-now)       ;Value 14: (not-empty-now) 
1 ]=> (q 'empty-queue?)                         ;Value: #f

练习 3.23

实现双端队列，两头都可以出队和入队。

; ptr selector
(define (front-ptr deque)
    (car deque))

(define (rear-ptr deque)
    (cdr deque))

; ptr setter
(define (set-front-ptr! deque item)
    (set-car! deque item))

(define (set-rear-ptr! deque item)
    (set-cdr! deque item))

; deque constructor
(define (make-deque)
    (cons '() '()))

; deque selector
(define (empty-deque? deque)
    (null? (front-ptr deque)))

(define (front-deque deque)
    (if (empty-deque? deque)
        (error "FRONT-DEQUE called with an empty deque" deque)
        (car (front-ptr deque))))

(define (rear-deque deque)
    (if (empty-deque? deque)
        (error "REAR-DEQUE called with an empty deque" deque)
        (car (rear-ptr deque))))

; deque setter
(define (insert-rear-deque! deque item)
    (let ((new-pair (cons item '())))
        (cond ((empty-deque? deque)
                (set-front-ptr! deque new-pair)
                (set-rear-ptr! deque new-pair)
                deque)
              (else
                (set-cdr! (rear-ptr deque) new-pair)
                (set-rear-ptr! deque new-pair)
                deque))))

(define (delete-front-deque! deque)
    (cond ((empty-deque? deque)
            (error "DELETE-FRONT-DEQUE! called with an empty deque" deque))
          (else
            (set-front-ptr! deque (cdr (front-ptr deque)))
            deque)))

(define (insert-front-deque! deque item)
    (cond ((empty-deque? deque)
            (insert-rear-deque! deque item))
          (else
            (set-front-ptr! deque (cons item (front-ptr deque)))
            deque)))

(define (delete-rear-deque! deque)
    (define (iter deque lst)
        (cond ((null? (cdr (cdr lst)))
                (set-cdr! lst '())
                (set-rear-ptr! deque lst)
                deque)
              (else
                (iter deque (cdr lst)))))
    (cond ((empty-deque? deque)
            (error "DELETE-REAR-DEQUE! called with an empty deque" deque))
          ((null? (cdr (front-ptr deque)))      ; 长度等于 1
            (set-front-ptr! deque '())
            deque)
          (else
            (iter deque (front-ptr deque)))))   ; 长度大于 1

(define (print-deque deque)
    (car deque))
    

1 ]=> (define q (make-deque))       ; 创建队列 ;Value: q 
1 ]=> (insert-front-deque! q 2)     ; 插入三个元素 ;Value 11: ((2) 2) 
1 ]=> (insert-front-deque! q 1)     ;Value 11: ((1 2) 2) 
1 ]=> (insert-rear-deque! q 3)      ;Value 11: ((1 2 3) 3) 
1 ]=> (print-deque q)               ;Value 12: (1 2 3) 
1 ]=> (delete-front-deque! q)       ; 从前端删除 ;Value 11: ((2 3) 3) 
1 ]=> (print-deque q)               ;Value 13: (2 3) 
1 ]=> (delete-rear-deque! q)        ; 从后端删除 ;Value 11: ((2) 2) 
1 ]=> (print-deque q)               ;Value 13: (2) 
1 ]=> (empty-deque? q)              ; 空队列测试 ;Value: #f 
1 ]=> (delete-rear-deque! q)        ;Value 11: (() 2) 
1 ]=> (empty-deque? q)              ;Value: #t 

双端队列的双链表实现

前面的双端队列实现虽然能满足功能上的目的，但是它不符合题目 『所有操作都必须在\(\Theta(1)\)步内完成』的要求，因为在delete-rear-deque!过程中 ，使用了一个\(\Theta(n)\)步的遍历操作。

需要修改双端队列的底层实现，从原来的单链表(single linked list)表示改为双链表 (double linked list)表示。

首先实现双链表：

;;; 23-double-linked-list.scm

(define (make-double-linked-list)
    '())

(define (empty-double-linked-list? lst)
    (null? lst))

(define (insert-double-linked-list! lst item)
    (cond ((empty-double-linked-list?)
            (set! lst (make-node item '() '()))
            lst)
          (else

表格的表示

一维表

类似key-value形式，还带一个特殊符号*table*作为哑记录：

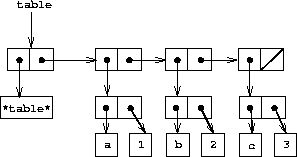
按key取记录的操作：

;; 按key取value
(define (lookup key table)
  (let ((record (assoc key (cdr table))))
    (if record
        (cdr record)     ;; 返回找到序对的value
        false)))

;; 找到所在的序对
(define (assoc key records)
  (cond ((null? records) false)
        ((equal? key (caar records)) (car records))
        (else (assoc key (cdr records)))))

增加key-value：

(define (insert! key value table)
  (let ((record (assoc key (cdr table))))
    (if record
        (set-cdr! record value)
        (set-cdr! table
                  (cons (cons key value) (cdr table)))))
  'ok)

创建表，只建立带*table*符号的列表：

(define (make-table) (list '*table*))

二维表格

带两级索引：

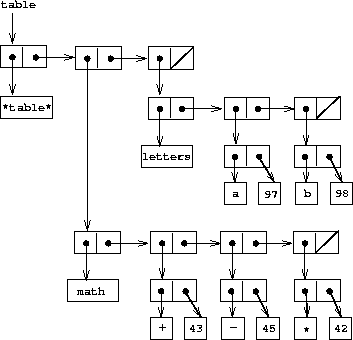
查找时先确认第一级的key，再确认第二级的key：

(define (lookup key-1 key-2 table)
  (let ((subtable (assoc key-1 (cdr table))))
    (if subtable
        (let ((record (assoc key-2 (cdr subtable))))
          (if record
              (cdr record)
              false))
        false)))

插入时，也要检查每一级的表格是否已经存在：

(define (insert! key-1 key-2 value table)
  (let ((subtable (assoc key-1 (cdr table))))
    (if subtable
        (let ((record (assoc key-2 (cdr subtable))))
          (if record
              (set-cdr! record value)
              (set-cdr! subtable
                        (cons (cons key-2 value)
                              (cdr subtable)))))
        (set-cdr! table
                  (cons (list key-1
                              (cons key-2 value))
                        (cdr table)))))
  'ok)

创建局部表格

为了说明查找和插入操作是在哪张表格上进行，上面的过程都需要一个表格参数。

另一种方法是以过程来表示表格，这样可以把操作作为表格的内部方法：

(define (make-table)
  (let ((local-table (list '*table*)))
    ;; 查找
    (define (lookup key-1 key-2)
      (let ((subtable (assoc key-1 (cdr local-table))))
        (if subtable
            (let ((record (assoc key-2 (cdr subtable))))
              (if record
                  (cdr record)
                  false))
            false)))
    ;; 插入
    (define (insert! key-1 key-2 value)
      (let ((subtable (assoc key-1 (cdr local-table))))
        (if subtable
            (let ((record (assoc key-2 (cdr subtable))))
              (if record
                  (set-cdr! record value)
                  (set-cdr! subtable
                            (cons (cons key-2 value)
                                  (cdr subtable)))))
            (set-cdr! local-table
                      (cons (list key-1
                                  (cons key-2 value))
                            (cdr local-table)))))
      'ok)    
    ;; 消息传递模式的转发器
    (define (dispatch m)
      (cond ((eq? m 'lookup-proc) lookup)
            ((eq? m 'insert-proc!) insert!)
            (else (error "Unknown operation -- TABLE" m))))
    ;; 返回操作
    dispatch))

对get和put方法的调用：

(define operation-table (make-table))

(define get (operation-table 'lookup-proc))   ;; 相当间接调用 lookup

(define put (operation-table 'insert-proc!))  ;; 相当于间接调用 insert!

练习 3.24

通过key取value的过程中，一般用equals?判断key是否相等。改进这一过程， 实现可以提供same-key?过程参数自定义判断key是否相等的逻辑。

增加了一个same-key?参数，而且要将这个same-key?闭包进assoc过程中：

(define (make-table same-key?)
    (let ((local-table (list '*table*)))
        (define (assoc key records)
            (cond ((null? records)
                    #f)
                  ((same-key? key (caar records))   ; 使用 same-key? 对比键
                    (car records))
                  (else
                    (assoc key (cdr records)))))
        (define (lookup key-1 key-2)
            (let ((subtable (assoc key-1 (cdr local-table))))
                (if subtable
                    (let ((record (assoc key-2 (cdr subtable))))
                        (if record
                            (cdr record)
                            #f))
                    #f)))
        (define (insert! key-1 key-2 value)
            (let ((subtable (assoc key-1 (cdr local-table))))
                (if subtable
                    (let ((record (assoc key-2 (cdr subtable))))
                        (if record
                            (set-cdr! record value)
                            (set-cdr! subtable
                                      (cons (key-2 value)
                                            (cdr subtable)))))
                    (set-cdr! local-table
                              (cons (list key-1
                                          (cons key-2 value))
                                    (cdr local-table)))))
            'ok)
        (define (dispatch m)
            (cond ((eq? m 'lookup-proc) lookup)
                  ((eq? m 'insert-proc!) insert!)
                  (else 
                    (error "Unknown operation -- TABLE" m))))
        dispatch))


1 ]=> (define number-table (make-table =))       ; 以数字为关键字的表
;Value: number-table

1 ]=> ((number-table 'insert-proc!) 10086 10086 'hello-moto) ;Value: ok
1 ]=> ((number-table 'lookup-proc) 10086 10086)              ;Value: hello-moto

1 ]=> (define symbol-table (make-table eq?))     ; 以符号为关键字的表
;Value: symbol-table

1 ]=> ((symbol-table 'insert-proc!) 'peter 'age 25)    ;Value: ok 
1 ]=> ((symbol-table 'lookup-proc) 'peter 'age)        ;Value: 25

练习 2.25

练习 2.26

练习 2.27

数字电路的模拟

基本的结构是门：

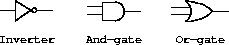
但门是用来改变信号的，信号不是存在门里的，是存在线路里的。 线路的构造函数是make-wire（先不关心具体实现）：

make-wire                ;; ok

以一个半加器为例：

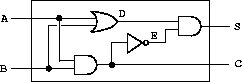
先把线路构造出来：

(define a (make-wire))
(define b (make-wire))
(define c (make-wire))
(define d (make-wire))
(define e (make-wire))
(define s (make-wire))

再把门构造出来，各种门构造函数的参数就每个端口上连的线，先不关心各种门的实现。

按半加器的线路结构把门和线连起来：

(or-gate  a b d)        ;; ok 
(and-gate a b c)        ;; ok 
(inverter c e)          ;; ok 
(and-gate d e s)        ;; ok

也可以把以上的代码包装为一个过程half-adder，参数是输入输出线路：

(define (half-adder a b s c)
  (let ((d (make-wire)) (e (make-wire)))
    (or-gate a b d)
    (and-gate a b c)
    (inverter c e)
    (and-gate d e s)
    'ok))

进一步可以实现全加器full-adder，参数是输入输出线路：

(define (full-adder a b c-in sum c-out)
  (let ((s (make-wire))
        (c1 (make-wire))
        (c2 (make-wire)))
    (half-adder b c-in s c1)
    (half-adder a s sum c2)
    (or-gate c1 c2 c-out)
    'ok))

基本功能块

先不管线路的构造函数，考虑一下线路的几个基本操作：

返加线上的值：

(get-signal <wire>)

设置线上的值：

(set-signal! <wire> <new value>)

当线上的值改变时，要调用的过程：

(add-action! <wire> <procedure of no arguments>)

模拟信号传播的时延，时延以后要调用对应的过程：

(after-delay <delay-time> <procedure of no arguments>)

实现非门：

(define (inverter input output)
  (define (invert-input)
    (let ((new-value (logical-not (get-signal input)))) ;; 把输入的信号作逻辑非
      (after-delay inverter-delay          ;; 传播时延值在变量inverter-delay里
                   (lambda () (set-signal! output new-value)))))
  (add-action! input invert-input)
  'ok)

;; 逻辑非
(define (logical-not s)
  (cond ((= s 0) 1)
        ((= s 1) 0)
        (else (error "Invalid signal" s))))

实现与门：

(define (and-gate a1 a2 output)
  (define (and-action-procedure)
    (let ((new-value
           (logical-and (get-signal a1) (get-signal a2))))
      (after-delay and-gate-delay
                   (lambda ()
                     (set-signal! output new-value)))))
  (add-action! a1 and-action-procedure) ;; 两个输入线都要触发事件
  (add-action! a2 and-action-procedure) ;; 两个输入线都要触发事件
  'ok)

;; 逻辑与
(define (logical-and x y)
	(cond ((and (not (= x 0)) (not (= x 1))) (error "Invalid signal" x))
	      ((and (not (= y 0)) (not (= y 1))) (error "Invalid signal" y))
        (else (if (and (= x 1) (= y 1)) 1 0))))

练习 2.28 实现或门

(define (or-gate input-1 input-2 output)
    (define (or-action-procedure)
        (let ((new-value
                (logical-or (get-signal input-1) (get-signal input-2))))
            (after-delay or-gate-delay
                         (lambda ()
                            (set-signal! output new-value)))))
    (add-action! input-1 or-action-procedure)
    (add-action! input-2 or-action-procedure)
    'ok)

(define (logical-or x y)
	(cond ((and (not (= x 0)) (not (= x 1))) (error "Invalid signal" x))
	      ((and (not (= y 0)) (not (= y 1))) (error "Invalid signal" y))
	      (else (if (or (= x 1) (= y 1)) 1 0))))

练习 2.29 De Morgan定律

根据 De Morgan 定律可知系：

\begin{equation} \begin{split} x \lor y = \lnot (\lnot x \land \lnot y) \end{split} \end{equation}

这也就是说可以在只使用and-gate和inverter的情况下，定义or-gate：

(define (or-gate input-1 input-2 output)
    (let ((invert-1 (make-wire))
          (invert-2 (make-wire))
          (and-invert-1-invert-2 (make-wire)))
        (inverter input-1 invert-1)
        (inverter input-2 invert-2)
        (and-gate invert-1 invert-2 and-invert-1-invert-2)
        (inverter and-invert-1-invert-2 output))
    'ok)

因为这个or-gate定义只是单纯的调用and-gate和inverter，所以它的延迟值由 and-gate-delay和inverter-delay决定。

整个or-gate共调用了三次inverter，一次and-gate， 因为有两个inverter是并行执行的，所以or-gate的延迟等于 。

\begin{equation} \begin{split} 3 \times \text{inverter-delay} + \text{and-gate-delay} \end{split} \end{equation}

or-gate 的另一个定义：

前面说过，logical-or的定义可以由布尔关系 \(x \lor y = \lnot (\lnot x \land \lnot y)\)给出，而其中的\(\lnot (a \land b)\) 又可以表示为另一个逻辑操作logical-nand，那么就得出了新的logical-or定义： x ∨ y = ¬x | ¬y ，其中符号 | 表示求两布尔值的 logical-nand 。

\begin{equation} \begin{split} x \lor y = \lnot x \lor \lnot y \end{split} \end{equation}

根据以上关系，可以给出相应的 nand-gate 定义， 因为这个nand-gate定义并不存在于书本中，所以我们需要（自作主张地）设置一个 nand-gate-delay：

(define nand-gate-delay 3)

(define (nand-gate input-1 input-2 output)
    (define (nand-action-procedure)
        (let ((new-value
                (logical-nand (get-signal input-1) (get-signal input-2))))
            (after-delay nand-gate-delay
                         (lambda ()
                            (set-signal! output new-value)))))
    (add-action! input-1 nand-action-procedure)
    (add-action! input-2 nand-action-procedure)
    'ok)

(define (logical-nand x y)
    (if (and (= x 1) (= y 1))
        0
        1))

确定nand-gate可以正常运行之后，就可以使用它来重定义or-gate了：

(define (or-gate input-1 input-2 output)
    (let ((invert-1 (make-wire))
          (invert-2 (make-wire)))
        (inverter input-1 invert-1)
        (inverter input-1 invert-2)
        (nand-gate invert-1 invert-2 output)))

练习 3.30 加法器与进位

全加器用进位串起来：

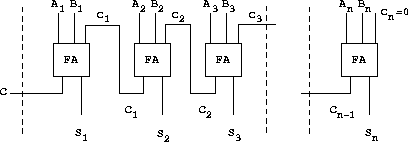
每个端口(A B S C)都有编号从1到n，比如（s1, s2, sn ）：

(define (dd x) (display x) (display " "))
(load "3.3.4.scm")

;; delay = (* n fa-delay)
;;       = (* n (+ ha-delay ha-delay or-delay))
;;       = (* n (+ (* 2 (+ (max and-delay (+ or-delay not-delay)) and-delay)) or-delay))

(define (ripple-carry-adder A B S C) ; assuming that A/B/S have the same length
    (define (adder A B c-in S c-out)
        (if (null? A)
            (add-action! c-in
                (lambda () (set-signal! C (get-signal c-in))))
            (let ((a (car A))
                  (b (car B))
                  (s (car S)))
                (full-adder a b c-in s c-out)
                (adder (cdr A) (cdr B) c-out (cdr S) (make-wire)))))
    (define c-in (make-wire))
    (set-signal! c-in 0)
    (adder A B c-in S (make-wire)))

;; tests
(define a0 (make-wire))
(define b0 (make-wire))
(define s0 (make-wire))

(define a1 (make-wire))
(define b1 (make-wire))
(define s1 (make-wire))

(define C (make-wire))

(ripple-carry-adder (list a0 a1) (list b0 b1) (list s0 s1) C)

(set-signal! a0 1)
(set-signal! a1 1)

(set-signal! b0 1)
(set-signal! b1 1)

(display (list (get-signal s0) (get-signal s1) (get-signal C)))

线路表示

线路主要存储两个内容：

• signal-value：信号的值。
• action-procedures：当信号改变时要触发的过程列表。

这里的实现方式是把操作的类型作为符号传给dispatch方法：

(define (make-wire)
  (let ((signal-value 0) (action-procedures '())) ;; 初始信号与事件列表为空

    ;; 设置信号的值
    (define (set-my-signal! new-value)
      (if (not (= signal-value new-value))       ;; 信号有改变
          (begin (set! signal-value new-value)   ;; 改变信号的值
                 (call-each action-procedures))  ;; 调用每一个事件
          'done))

    ;; 添加事件到事件列表
    (define (accept-action-procedure! proc)
      (set! action-procedures (cons proc action-procedures))
      (proc))                                    ;; 注意这里要立即执行

    ;; 分发事件，实现操作
    (define (dispatch m)
      (cond ((eq? m 'get-signal) signal-value)
            ((eq? m 'set-signal!) set-my-signal!)
            ((eq? m 'add-action!) accept-action-procedure!)
            (else (error "Unknown operation -- WIRE" m))))

    dispatch)) ;; dispatch作为返回值

调用每个事件的call-each过程实现如下：

(define (call-each procedures)
  (if (null? procedures)
      'done
      (begin
        ((car procedures))
        (call-each (cdr procedures)))))

线路的具体操作：

(define (get-signal wire)
  (wire 'get-signal))
  
(define (set-signal! wire new-value)
  ((wire 'set-signal!) new-value))
  
(define (add-action! wire action-procedure)
  ((wire 'add-action!) action-procedure))

待处理列表

after-delay用来实现在时延以后执行指定的任务。

实现的方法是用一个日程表（agenda）存储要执行的执行的和时间，它的主要操作有：

(make-agenda)                              ;; 构造函数

(empty-agenda? <agenda>)

(first-agenda-item <agenda>)               ;; 取第一个任务

(remove-first-agenda-item! <agenda>)       ;; 删除第一个任务

(add-to-agenda! <time> <action> <agenda>)  ;; 添加任务到列表

(current-time <agenda>)                    ;; 当前系统模拟时间

通过向日程表添加任务，就可以实现after-delay：

(define (after-delay delay action)
  (add-to-agenda! (+ delay (current-time the-agenda))
                  action
                  the-agenda))

实现propagate过程来实现按顺序执行日程表中日程的操作：

(define (propagate)
  (if (empty-agenda? the-agenda)
      'done
      (let ((first-item (first-agenda-item the-agenda)))
        (first-item)
        (remove-first-agenda-item! the-agenda)
        (propagate))))                           ;; 递归调用，执行下一轮

一个简单的实例模拟

定义探针（probe）监视一个线路的值：

(define (probe name wire)
  (add-action! wire
               (lambda ()        
                 (newline)
                 (display name)                      ;; 显示线路名
                 (display " ")
                 (display (current-time the-agenda)) ;; 时间与执行的任务
                 (display "  New-value = ")
                 (display (get-signal wire)))))      ;; 显示线路的值

初始化各实例：

(define the-agenda (make-agenda)) ;; 初始化日程表为空

(define inverter-delay 2)         ;; 定义非门的时延
(define and-gate-delay 3)         ;; 定义与门的时延
(define or-gate-delay 5)          ;; 定义非门的时延

创建线路，并在线路上加上探针：

(define input-1 (make-wire))
(define input-2 (make-wire))

(define sum   (make-wire))
(define carry (make-wire))

(probe 'sum sum)        ;; sum 0  New-value = 0
(probe 'carry carry)    ;; carry 0  New-value = 0

连接线路到半加器上：

(half-adder input-1 input-2 sum carry)   ;; ok

(set-signal! input-1 1)                  ;; done

(propagate)                              ;; sum 8  New-value = 1
                                         ;; 在时间到8时，sum上的信号为1。
                                         ;; done

手动改变input-2上的信号为1，观察让信号传播情况：

(set-signal! input-2 1)                  ;; done

(propagate)                              ;; carry 11  New-value = 1
                                         ;; sum   16  New-value = 0
                                         ;; done

练习 3.31

make-wire中定义了内部过程：

;; 添加事件到事件列表
(define (accept-action-procedure! proc)
  (set! action-procedures (cons proc action-procedures))
  (proc))                                    ;; 注意这里要立即执行

为什么要立即执行？如果去掉立即执行这一句会怎么样？

先说对应的现实意义：当你将两个点连接起来的时候，应该马上会起作用。

但是在set-my-signal!里，只有信号变了才会有触发事件。

(define (set-my-signal! new-value)
  (if (not (= signal-value new-value))
    (begin
      (set! signal-value new-value)
      (call-each action-procedures))
    'done))

也就是说，如果后续设置的信号与当前信号相同的话不会有任何改变。

加入把accept-action-procedure!里的(proc)去掉，那么信号的初始状态不会反映到 现在的电路中。于是就引出问题了：

由于(make-wire)的时候设置的是默认值0，那么后续给它的值还是0的话， 这个电路就不会有任何变化，这不符合电路的工作预期，导致了错误的结果。

当然，如果一定要把(proc)去掉也没可以，我们可以认为初始状态下信号的值是 没有意义的，但是需要set-my-signal!里面的判断条件去掉，无条件执行 (call-each action-procedures)，这样再设置信号的时候就会得到预期的反应。

实现待处理列表

待处理列表中的元素是「时间段」，时间段的结构为「时间」和「任务队列」组成， 意味着同一时间点要要执行的任务，具体的实现为：

(define (make-time-segment time queue)
  (cons time queue))

(define (segment-time s) (car s))

(define (segment-queue s) (cdr s))

待处理列表作为时间段的容器，是以之前实现的一维表格实现的。但主要区别有：

1. 之前的一维表例子不用存额外的信息，所以表头是一个空的*table*标记。在这里， 我们要把「当前的时间」存在表头里，因为我们只处理未来的事件。
2. 表里所有的时间段都是按时间递增排序的。

;; 创建表，当前时间初始化为0
(define (make-agenda) (list 0))

;; 表头里的当前模拟时间
(define (current-time agenda) (car agenda))

;; 更改表头里的当前模拟时间
(define (set-current-time! agenda time)
  (set-car! agenda time))

;; 表里的所有时间段
(define (segments agenda) (cdr agenda))

;; 设置表里的时间段
(define (set-segments! agenda segments)
  (set-cdr! agenda segments))

;; 表里第一个时间段
(define (first-segment agenda) (car (segments agenda)))

;; 表里第一个外的其他所有时间段
(define (rest-segments agenda) (cdr (segments agenda)))

;; 表里的时间段是否为空
(define (empty-agenda? agenda) (null? (segments agenda)))

添加时间段到表里：

(define (add-to-agenda! time action agenda)

  ;; 新动作的时间小于表里的最小的时间
  (define (belongs-before? segments)
    (or (null? segments)
        (< time (segment-time (car segments)))))

  ;; 创建新的时间段
  (define (make-new-time-segment time action)
    (let ((q (make-queue)))
      (insert-queue! q action)       ;; 新时间段的队列是空的
      (make-time-segment time q)))   ;; 把操作添加到空的队列里

  ;; 把操作添加到时间段里
  (define (add-to-segments! segments)
    (if (= (segment-time (car segments)) time)
        ;; 如果时间对得上，就把事件加到这个时间段里
        (insert-queue! (segment-queue (car segments))
                       action)
        ;; 如果时间对不上
        (let ((rest (cdr segments)))
          (if (belongs-before? rest)
              ;; 新的时间比表里最小的时间还要早，
							;; 创建一个新最小的时间段加在表头上
              (set-cdr!  segments
                         (cons (make-new-time-segment time action)
                               (cdr segments)))
              ;; 新的时间并不比表里最小的时间还要早，
              ;; 继续向下遍历表
              (add-to-segments! rest)))))

  ;; 主逻辑
  (let ((segments (segments agenda))) ;; 取表身里的所有时间段作为变量segments
    (if (belongs-before? segments)
        ;; 如果新加的时间比表里早，加到头上
        (set-segments!
          agenda
          (cons (make-new-time-segment time action)
                segments))
        ;; 如果新加的时间不比表里更早，遍历剩下的表
        (add-to-segments! segments))))

实现从表里删除一个操作的功能（注意是删除操作不是删除时间段）：

(define (remove-first-agenda-item! agenda)
  (let ((q (segment-queue (first-segment agenda))))
    (delete-queue! q)
    (if (empty-queue? q) ;; 如果这个时间段已经空了，把时间段也删除
        (set-segments! agenda (rest-segments agenda)))))

实现取表里第一个时间段的第一项的操作（注意要更新模拟当前时间）：

(define (first-agenda-item agenda)
  (if (empty-agenda? agenda)
      (error "Agenda is empty -- FIRST-AGENDA-ITEM")
      (let ((first-seg (first-segment agenda)))  ;; 第一个时间段
        (set-current-time! agenda (segment-time first-seg)) ;; 更新当前时间
        (front-queue (segment-queue first-seg)))))

练习 3.32

在这里用的是队列，如果改为栈会有什么区别？在与门为例子，它的输入从(0,1)变为 (1, 0)。

Queue(FIFO):

[front]-> ((set-signal! A 0) (set-signal! B 1) (set-signal! A 1) (set-signal! B 0))

从front开始执行，最终A、B的状态是(1, 0)

Stack(FILO):

[front]-> ((set-signal! B 0) (set-signal! A 1) (set-signal! B 1) (set-signal! A 0))

从front开始执行，最终A、B的状态是(0, 1)不符合预期。

约束的传播

约束系统可以描述约束关系。

以华氏度与摄氏度的关系为例：

\[ \begin{equation} 9C=5(F - 32) \end{equation} \]

用之前介绍的方法写程序，要写「根据1C求F」和「根据F求C」两个程序； 利用约束系统，\(C\)与\(F\)只要知道一个就可以自动求出另外一个。

用图来描述：

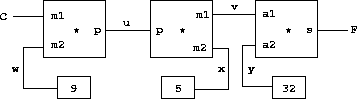
图例说明：

• 中间为*的方框为约束。每个约束有端口表示不同值的关系。
  • 乘法约束有两个代表相乘数的端口m1、m2和代表结果的端口p。
  • 加法约束有两个代表相乘数的端口a1、a2和代表结果的端口s。
• 线条为连接器，把值对应起来。
• 带数字的小方块为常量。

工作过程：

1. 线条（连接器）在赋值以后会唤醒所有相连的约束。
2. 被唤醒的约束盘点所有相连的连接器，检查是否已经有足够的信息确定一个值。
3. 如果够多，就给那个连接器赋值。

约束系统的使用

先不考虑连接器（连线）的构造函数make-connector如何实现， 按需求它们的任务是构造连接器：

(define C (make-connector))          ;; 创建摄氏度
(define F (make-connector))          ;; 创建华氏度

然后要有一个摄氏度与华氏度的约束的构造函数celsius-fahrenheit-converter：

(define (celsius-fahrenheit-converter c f)
  (let ((u (make-connector))   ;; 构造本约束内部的连线
        (v (make-connector))
        (w (make-connector))
        (x (make-connector))
        (y (make-connector)))
    (multiplier c w u)         ;; 内部的乘法约束和加法约束
    (multiplier v x u)
    (adder v y f)
    (constant 9 w)             ;; 内部的常量
    (constant 5 x)
    (constant 32 y)
    'ok))

(celsius-fahrenheit-converter C F)   ;; 构造一个温度转化约束的实例
                                     ;; ok

还需要探针检查值的变量（先不考虑实现）：

(probe "Celsius temp" C)      ;; 构造探针监视连接器
(probe "Fahrenheit temp" F)

还有在set-value!过程来改变连接器上的值，它的第三个参数表示值的来源， ：

(set-value! C 25 'user)       ;; 这里 'user 表示是用户手动设置的
                              ;;
                              ;; 设置连接器值的时候，探针返回线上的值
                              ;; Probe: Celsius temp = 25
                              ;; Probe: Fahrenheit temp = 77
                              ;; done

连接器上的值应该由约束推导出来，所以当用户手动设置一个已经有值的连接器时， 系统应该报错，一定要先用for-value!强制清除掉原来的值：

(set-value! F 212 'user)      ;; Error! Contradiction (77 212)

(forget-value! C 'user)       ;; Probe: Celsius temp = ?
                              ;; *注意* 这里删除了C会传播到F：
                              ;; Probe: Fahrenheit temp = ?
                              ;; done

约束系统的实现

约束系统比模拟电路程序简单，因为不用考虑时迟。

基本的连接器功能包括：

(has-value? <connector>)   ;; 是否有值

(get-value <connector>)    ;; 取值

;; 信息源informat要求把connector的值设置为new-calue
(set-value! <connector> <new-value> <informant>)  

;; retractor要求消除connector的值
(forget-value! <connector> <retractor>)

;; 连接器边到约束上
(connect <connector> <new-constraint>)

加法器的实现：

(define (adder a1 a2 sum)

  ;; 计算机约束操作
  (define (process-new-value)
    ;; 三个值里只要有两个就可以推出第三个
    (cond ((and (has-value? a1) (has-value? a2))
           (set-value! sum
                       (+ (get-value a1) (get-value a2))
                       me))
          ((and (has-value? a1) (has-value? sum))
           (set-value! a2
                       (- (get-value sum) (get-value a1))
                       me))
          ((and (has-value? a2) (has-value? sum))
           (set-value! a1
                       (- (get-value sum) (get-value a2))
                       me))))

  ;; 当有连接器的值被清除时
  (define (process-forget-value)
    (forget-value! sum me)  ;; 清除所有的连接器的值
    (forget-value! a1 me)
    (forget-value! a2 me)
    (process-new-value))    ;; 重新计算一遍约束

	;; 操作转发
  (define (me request)
    (cond ((eq? request 'I-have-a-value)  
           (process-new-value))
          ((eq? request 'I-lost-my-value) 
           (process-forget-value))
          (else 
           (error "Unknown request -- ADDER" request))))

  ;; 连接约束与连接器
  (connect a1 me)
  (connect a2 me)
  (connect sum me)
  me)

;; 外部的操作界面：

(define (inform-about-value constraint)
  (constraint 'I-have-a-value))

(define (inform-about-no-value constraint)
  (constraint 'I-lost-my-value))

乘法操作的实现：

(define (multiplier m1 m2 product)

  (define (process-new-value)
    (cond ((or (and (has-value? m1) (= (get-value m1) 0))
               (and (has-value? m2) (= (get-value m2) 0)))
           (set-value! product 0 me)) ;; 相乘的两数有一个为0结果一定为0
          ((and (has-value? m1) (has-value? m2))
           (set-value! product
                       (* (get-value m1) (get-value m2))
                       me))
          ((and (has-value? product) (has-value? m1))
           (set-value! m2
                       (/ (get-value product) (get-value m1))
                       me))
          ((and (has-value? product) (has-value? m2))
           (set-value! m1
                       (/ (get-value product) (get-value m2))
                       me))))

  (define (process-forget-value)
    (forget-value! product me)
    (forget-value! m1 me)
    (forget-value! m2 me)
    (process-new-value))

  (define (me request)
    (cond ((eq? request 'I-have-a-value)
           (process-new-value))
          ((eq? request 'I-lost-my-value)
           (process-forget-value))
          (else
           (error "Unknown request -- MULTIPLIER" request))))

  ;; 连接约束与连接器
  (connect m1 me)
  (connect m2 me)
  (connect product me)
  me)

常量就是不能赋值的约束：

(define (constant value connector)
  (define (me request)
    (error "Unknown request -- CONSTANT" request))
  (connect connector me)
  (set-value! connector value me)
  me)

探针的实现：

(define (probe name connector)

  ;; 显示值
  (define (print-probe value)
    (newline)
    (display "Probe: ")
    (display name)
    (display " = ")
    (display value))

  
  ;; 有新值时显示值
  (define (process-new-value)
    (print-probe (get-value connector)))

  ;; 删除值时也显示值
  (define (process-forget-value)
    (print-probe "?"))

	;; 操作转发
  (define (me request)
    (cond ((eq? request 'I-have-a-value)
           (process-new-value))
          ((eq? request 'I-lost-my-value)
           (process-forget-value))
          (else
           (error "Unknown request -- PROBE" request))))
  (connect connector me)
  me)

连接器的表示

(define (make-connector)
  ;; 连接器需要有内部状态：
  (let ((value false)      ;; 值
        (informant false)  ;; 值是哪个对象设置的，如果为false表示值为空
        (constraints '())) ;; 所有连接的约束列表
    
		;; 赋值
    (define (set-my-value newval setter)
      (cond ((not (has-value? me))
             (set! value newval)
             (set! informant setter)
             ;; 通知所有的约束，有一个值已经变了
             (for-each-except setter
                              inform-about-value
                              constraints))
            ;; 已经有值了不能改
            ((not (= value newval))
             (error "Contradiction" (list value newval)))
            (else 'ignored)))
    
		;; 清除值 
    (define (forget-my-value retractor)
      (if (eq? retractor informant)
          (begin (set! informant false) ;; informat为false表示没有值
                 ;; 通知所有的约束，有一个值被清了
                 (for-each-except retractor
                                  inform-about-no-value
                                  constraints))
          'ignored))
    
		;; 连接到一个约束
    (define (connect new-constraint)
      (if (not (memq new-constraint constraints))
          (set! constraints 
                (cons new-constraint constraints)))
      (if (has-value? me)
          (inform-about-value new-constraint))
      'done)
    
		;; 操作转发
    (define (me request)
      (cond ((eq? request 'has-value?)
              (if informant true false))
            ((eq? request 'value) value)
            ((eq? request 'set-value!) set-my-value)
            ((eq? request 'forget) forget-my-value)
            ((eq? request 'connect) connect)
            (else (error "Unknown operation -- CONNECTOR" request))))

    ;; 返回值
    me))

for-each-except会通知所有的约束有值变了，但是会跳过执行赋值操作的那个约束：

;; 参数：
;;     操作者
;;     操作类型：赋值还是清值
;;     约束列表
(define (for-each-except exception procedure list)
  (define (loop items)
    (cond ((null? items) 'done)
          ((eq? (car items) exception) (loop (cdr items)))
          (else (procedure (car items))
                (loop (cdr items)))))
  (loop list))

外部的操作界面：

(define (has-value? connector)
  (connector 'has-value?))

(define (get-value connector)
  (connector 'value))

(define (set-value! connector new-value informant)
  ((connector 'set-value!) new-value informant))

(define (forget-value! connector retractor)
  ((connector 'forget) retractor))

(define (connect connector new-constraint)
  ((connector 'connect) new-constraint))

练习 3.33

用加法约束与乘法约束组合新的约束：\(a\)与\(b\)的平均值\(c\)。

方法一：

\[ \begin{equation} (a + b) / 2 = c \end{equation} \]

(define (averager a b c)
    (let ((sum (make-connector))
          (d (make-connector)))
        (adder a b sum)
        (multiplier sum d c)
        (constant (/ 1 2) d)
        'ok))

; 设置连接器 
(define a (make-connector))  ;Value: a
(define b (make-connector))  ;Value: b
(define c (make-connector))  ;Value: c

; 监视连接器
(probe "a" a)                ;Value 11: #[compound-procedure 11 me]
(probe "b" b)                ;Value 12: #[compound-procedure 12 me]
(probe "c" c)                ;Value 13: #[compound-procedure 13 me]

; 进行约束
(averager a b c)             ;Value: ok 
(set-value! a 2 'user)       ; Probe: a = 2
                             ;Value: done
(set-value! b 4 'user)       ; Probe: c = 3
                             ; Probe: b = 4
                             ;Value: done
(get-value c)                ;Value: 3

方法二：

\[ \begin{equation} (a + b) = c \times 2 \end{equation} \]

(define (averager a b c)
    (let 
        ((mid (make-connector))
         (two (make-connector)))
        (adder a b mid)
        (multiplier c two mid)
        (constant 2 two)
        'ok))

(define a (make-connector))
(define b (make-connector))
(define c (make-connector))

(averager a b c)

(probe "a" a)
(probe "b" b)
(probe "c" c)

(set-value! a 3 'user)
(set-value! b 5 'user)

(forget-value! b 'user)
(set-value! c 8 'user)

练习 3.34

为了实现约束\(a^2 = b\)，为什么下面代码是错的？

(define (squarer a b)
  (multiplier a a b))

因为multiplier的m1和m2都是a，因此m1、m2都是没有value的， 约束条件不满足，约束无法从b传播至a。

练习 3.35

通过填空实现\(a^2 = b\)：

(define (squarer a b)
  (define (process-new-value)
    (if (has-value? b)
        (if (< (get-value b) 0)
            (error "square less than 0 -- SQUARER" (get-value b))
            <alternative1>)
        <alternative2>))
  (define (process-forget-value) <body1>)
  (define (me request) <body2>)
  <rest of definition>
  me)

实现：

(define (squarer a b)

    (define (process-new-value)
        (if (has-value? b)
            (if (< (get-value b) 0)
                (error "square less than 0 -- SQUARER" (get-value b))
                (set-value! a (sqrt (get-value b)) me))
            (if (has-value? a)
                (set-value! b (* (get-value a) (get-value a)) me))))

    (define (process-forget-value)
        (forget-value! a me)
        (forget-value! b me)
        (process-new-value))

    (define (me request)
        (cond
            ((eq? request 'I-have-a-value) (process-new-value))
            ((eq? request 'I-lost-my-value) (process-forget-value))
            (else (error "unknown request -- SQUARER.me" request))))

    (connect a me)
    (connect b me)
    me)

;#|

(define a (make-connector))
(define b (make-connector))

(squarer a b)
(probe "a" a)
(probe "b" b)

(set-value! a 3 'user)
(forget-value! a 'user)

(set-value! b 16 'user)

;|#

练习 3.36

当执行以下表达式序列时：

(define a (make-connector))
(define b (make-connector))
(set-value! a 10 'user)

在对set-value!求值某个时刻，其中有一步调用：

(for-each-except setter inform-about-value constraints)

画出这个表达式的求值环境模型图。

; (for-each-except setter inform-about-value constraints)
#|
(set-value! a 10 'user)
 -> ((a 'set-value!) 10 'user) => [set-value!: connector=a new-value=10 informant='user] => [GLOBAL]
     -> (set-my-value new-value informant) [make-connector: value=false informant=false constraints=()] => [GLOBAL]
         -> (not (has-value? me)) [set-my-value: newval=10 setter=user] => make-connector
                (set! value newval)
                (set! informant setter)
                (for-each-except setter inform-about-value constraints)
|#

练习 3.37 表达式风格的约束

之前的我们实现的约束语法比较麻烦，比如对于：

\[ \begin{equation} (a + b) \times (c + d) \end{equation} \]

描述为：

(v-sum a b temp1)
(v-sum c d temp2)
(v-prod temp1 temp2 answer)

可以换为以过程为返回值的写法，这样不用很多中间变量：

(define answer (v-prod (v-sum a b) (v-sum c d)))

把温度转换约束转为更加像运算风格的定义：

(define (celsius-fahrenheit-converter x)
  (c+ (c* (c/ (cv 9) (cv 5))
          x)
      (cv 32)))

(define C (make-connector))

(define F (celsius-fahrenheit-converter C))

比如重写的加法约束以两个连接器为参数，返回另一个连接器：

;; 加法约束
(define (c+ x y)
    (let ((z (make-connector)))
        (adder x y z)
        z))

;; 减法约束
(define (c- x y)
    (let ((z (make-connector)))
        (adder y z x)
        z))

;; 乘法约束
(define (c* x y)
    (let ((z (make-connector)))
        (multiplier x y z)
        z))

;; 除法约束
(define (c/ x y)
    (let ((z (make-connector)))
        (multiplier y z x)
        z))

;; 常量约束
(define (cv x)
    (let ((c (make-connector)))
        (constant x c)
        c))

;; 温度转换约束
(define (celsius-fahrenheit-converter x)
    (c+ (c* (c/ (cv 9) (cv 5))
            x)
        (cv 32)))

(define C (make-connector))
(define F (celsius-fahrenheit-converter C))

(probe "C" C)
(probe "F" F)

(set-value! C 25 'user)
(forget-value! C 'user)

(set-value! F 212 'user)