ch03 模块化、对象和状态 part05

流

流是一个采用了「延时求值技术」的序列，它可能缓和状态模拟过程中的复杂性。

流作为延时的表

延时求值的实现：

• (delay <exp>)生成延时求值对象。注意它是一个特殊语法而不是过程， 如果是过程的话作为参数的<exp>会在过程调用前先被求值，这样就不是延时求值了。　
• (force <exp>)执行延时求值对象，它可以用普通的过程来实现。

构造方法也是一个特殊形式，不然参数会在调用前先被求值：

(cons-stream <a> <b>)

相当于：

(cons <a> (delay <b>))

选择过程的实现：

(define (stream-car stream) (car stream))         ;; 直接返回头部

(define (stream-cdr stream) (force (cdr stream))) ;; 通过求值得到剩下的部分

在MIT实现中：

• the-empty-stream等于'()；
• stream-null?等于null?。

;; 取第n个元素
(define (stream-ref s n)
  (if (= n 0)
      (stream-car s)
      (stream-ref (stream-cdr s) (- n 1))))

;; 映射新流
(define (stream-map proc s)
  (if (stream-null? s)
      the-empty-stream
      (cons-stream (proc (stream-car s))
                   (stream-map proc (stream-cdr s)))))

;; 以每个元素为参数执行
(define (stream-for-each proc s)
  (if (stream-null? s)
      'done
      (begin (proc (stream-car s))
             (stream-for-each proc (stream-cdr s)))))

其中for-each过程在显示流内容时很有用：

;; 显示流的全部内容
(define (display-stream s)
  (stream-for-each display-line s))

;; 输出到一行
(define (display-line x)
  (newline)
  (display x))

流实现的行为方式

用流实现过滤素数的程序。

stream-enumerate-interval有流的方式生成区间内所有的整数：

(define (stream-enumerate-interval low high)
  (if (> low high)
      the-empty-stream
      (cons-stream low 
                   (stream-enumerate-interval (+ low 1)                         
                                              high))))
      

stream-filter实现对流的过滤功能：

;; pred : 过滤的规则
;; stream : 需要被过滤的流
(define (stream-filter pred stream)
  (cond ((stream-null? stream) the-empty-stream)
        ((pred (stream-car stream))                  ;; 如果符合条件
          (cons-stream (stream-car stream)           ;; 当前节点加入结果列表
                       (stream-filter pred           ;; 继续检查剩下的流
                                      (stream-cdr stream))))
        ;; 当前节点不符合，继续检查剩下的流
        (else (stream-filter pred (stream-cdr stream)))))

结合起来可以用流取出素数：

(stream-car
  (stream-cdr
    (stream-filter prime?
                   (stream-enumerate-interval 10000 1000000))))

delay和force的实现

delay是一个特殊语法而不是过程：

(delay <exp>)

它的功能相当于把结果作为lambda返回，相当于：　

(lambda () <exp>)

force则直接调用lambda（即直接调用delay的结果），可以用过程实现：

(define (force delayed-object)
  (delayed-object))

通过缓存技术还可以进一步优化，把第一次计算的结果保存起来：

(define (memo-proc proc)
  (let ((already-run? false) (result false))
    (lambda ()
      (if (not already-run?)
          (begin (set! result (proc))
                 (set! already-run? true)
                 result)
          result))))

这样以后可以把delay等价于：

(memo-proc (lambda () <exp>))

练习 3.50

下面这个强化版的定义可以允许过程带多个参数：

(define (stream-map proc . argstreams)
  (if (<??> (car argstreams))
      the-empty-stream
      (<??>
       (apply proc (map <??> argstreams))
       (apply stream-map
              (cons proc (map <??> argstreams))))))

实现：

(define (stream-map-multi proc . streams)
    (if (stream-null? (car streams))
        the-empty-stream
        (cons-stream
            (apply proc (map stream-car streams))
            (apply stream-map-multi (cons proc (map stream-cdr streams))))))

(display-stream
    (stream-map-multi
        +
        (stream-enumerate-interval 1 10)
        (stream-enumerate-interval 11 20)
        (stream-enumerate-interval 21 30)))

练习 3.51

以下过程会在打印参数以后，返回参数的值：

(define (show x)
          (display x)
          x)

观察以下调用过程：

只有流的stream-car部分被求值(延迟求值的效果)：

(define x (stream-map show (stream-enumerate-interval 0 10)))
0
;Value: x

只计算所需的值，不多也不少(延迟求值的效果)：

(stream-ref x 5)
12345
;Value: 5

只需计算 6 和 7 ，没有重复计算：

(stream-ref x 7)
67
;Value: 7

也就是说，force是有副作用的，实际上已经将promise计算结果记忆下来了， 使得下一次使用这个promise时不必再执行一次计算过程。

但是这也意味着，传递给delay的form不应该具有任何副作用，否则会产生非预期的结果。 (或者使用类似习题3-27的memorize函数来实现)

这里有一个解释delay和force的文档，以及一些很有意思的stream的例子。 http://people.cs.aau.dk/~normark/prog3-03/html/notes/eval-order_themes-delay-stream-section.html

练习 3.52

(define sum 0)

(define (accum x)
    (set! sum (+ x sum))
    sum)

(define seq (stream-map accum (stream-enumerate-interval 1 20)))
; (stream-map accum {1 (delay [2 20])})
; { (accum 1) (delay (stream-map accum {2 (delay [3 20])} )) } ;; sum = 1
; value: {1 (delay (stream-map accum {2 (delay [3 20]) )) }

(display "sum: ")
(display-line sum) ; 1

(define y (stream-filter even? seq))
; (stream-filter even? {1 (delay ...)} )
; (stream-filter even? (force (delay (stream-map accum {2 (delay [3 20])}))))
; (stream-filter even? { (accum 2) (delay (stream-map accum {3 (delay [4 20])} )) } ) ;; sum = sum + 2 = 3
; (stream-filter even? { (accum 3) (delay (stream-map accum {4 (delay [5 20])} )) } ) ;; sum = sum + 3 = 6
;                      ------------------------------------------------------------
;                                                   v
; { 6 (delay stream-filter? even? (stream-cdr! {3 (delay (stream-map (accum {4 (delay [5 20])} ))) })) }

(display "sum: ")
(display-line sum) ;6

(define mod5? (lambda (x) (= (remainder x 5) 0)))

(define z (stream-filter mod5? seq))
; (stream-filter mod5? {1 3 6 (delay (filter-even (map-accum (enumerate 4 10))))}
; ...
; (filter-mod5 {(accum 4) (filter-even (map-accum (enumerate 5 10)))}) ;; sum = sum + 4 = 10
;

(display "sum: ")
(display-line sum) ;10

(stream-ref y 7) ;value: 136
; {1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 [17 20]}
; seq: {1 3 6 10 15 21 28 36 45 55 66 78 91 105 120 136 [...]} 
; y: {6 10 28 36 66 78 120 136}
; sum = 136

(display "sum: ")
(display-line sum) ;136

(display-stream z)
; seq: { ... 120 136 153 171 190 210}
; z: {10 15 45 55 105 120 190 210}
; sum = 210
;
(display "sum: ")
(display-line sum) ;210

stream-ref的值为136，display-stream会输出z = {10..210}

如果delay的实现没有优化memo-proc，那么sum会被多次加入， 而且因为 define seq/y/z 的时候实际上已经计算了一些，因此sum的结果会很诡异。

无记忆的delay和force实现供参考：

#|
(define-syntax delay
     (syntax-rules ()
          [(delay x) (lambda () x)]))

(define (force promise)
     (promise))
|#

无穷流

整数流是无穷的：

;; 从n开始的整数流
(define (integers-starting-from n)
  (cons-stream n (integers-starting-from (+ n 1))))

;; 整数流
(define integers (integers-starting-from 1))

如果要得到能被整除的所有数：

;; 是x否可以被y整除
(define (divisible? x y) (= (remainder x y) 0))

;; 不可被7整队的所有整数
(define no-sevens
  (stream-filter (lambda (x) (not (divisible? x 7)))
                 integers))

;; 调用
(stream-ref no-sevens 100)               ;; 117

斐波那契数列也是无穷的：

(define (fibgen a b)
  (cons-stream a (fibgen b (+ a b))))

(define fibs (fibgen 0 1))

无穷流可以实现多塞筛法求素数：每找到一个素数，就可以把它的倍数都排除。

;; 过滤掉流中第一个素数的倍数
(define (sieve stream)
  (cons-stream
    (stream-car stream)       ;; 第一个元素
    (sieve (stream-filter     ;; 过滤到第一个元素的倍数
             (lambda (x)
               (not (divisible? x (stream-car stream))))
             (stream-cdr stream)))))

;; 所有的素数
(define primes (sieve (integers-starting-from 2)))

上面的效果相当于每取一个就套一层filter，如下图：

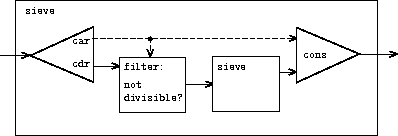
这种图被称为「Henderson图」，是一种思考流处理的试：

• 实线表示传输值的流。
• 虚线表示值，而不是流。

隐式地定义流

之前演示的都是通过描述「生成过程」的方式定义的，这些过程需要一个一个地计算机出 流的元素。

还有一种方式是隐式地定义流，比如这个无穷的「1」：

(define ones (cons-stream 1 ones))

这里的机制类似于递归：

• ones是一个序对，car为1。
• cdr是一个对ones求值的许诺。

可以把两个流的元素一一对应地相加起来：

(define (add-streams s1 s2)
  (stream-map + s1 s2))

通过这两个过程可以列出所有的整数：

(define integers (cons-stream 1 (add-streams ones integers)))

以上代码也是以类似递归调用的方式把对integers自身的求值许诺作为cdr部分。

同样的风格也可以生成斐波那契数列：

(define fibs
  (cons-stream 0
               (cons-stream 1
                            (add-streams (stream-cdr fibs)
                                         fibs))))

斐波那契数列的机制就是把前两个数相加，所以这里的方法类似于错位加相：

		1	1	2	3	5	8	13	21	\(\cdots\)	=	(stream-cdr fibs)
		0	1	1	2	3	5	8	13	\(\cdots\)	=	fibs
0	1	1	2	3	5	8	13	21	34	\(\cdots\)	=	fibs

另一个常用的场景，把指定的常数加到每一项上。比如生成2的各个幂：

;; 流stream中的每个元素都乘以指定的倍数factor
(define (scale-stream stream factor)
  (stream-map (lambda (x) (* x factor)) stream))

;; 生成2的所有幂
(define double (cons-stream 1 (scale-stream double 2))) ; 1, 2, 4, 8, 16, ...

生成素数流的另一个方法，从整数2开始，检查是否为素数来过滤它们：

(define primes
  (cons-stream
    2
    (stream-filter prime? (integers-starting-from 3))))

(define (prime? n)
  (define (iter ps)
    (cond ((> (square (stream-car ps)) n) true)
          ((divisible? n (stream-car ps)) false)
          (else (iter (stream-cdr ps)))))
  (iter primes))            ;; 递归调用了primes

练习 3.53

在不运行程序的情况下描述流里的元素：

(define s (cons-stream 1 (add-streams s s)))

解：

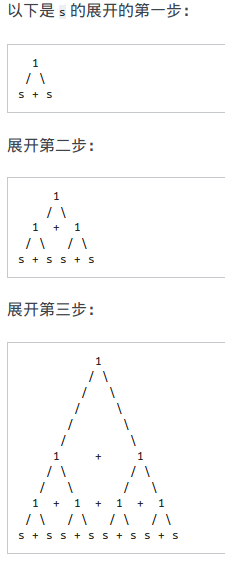
用程序验证：

1 ]=> (stream-head s 10)   ;Value 11: (1 2 4 8 16 32 64 128 256 512)

练习 3.54

实现过程mul-streams把两个流的元素相互乘积。再用它结合的integers实现 从n为零开始的，第n个元素是\((n+1)!\)的流：

(define factorials (cons-stream 1 (mul-streams <??> <??>)))

解：

(define (mul-streams s1 s2)
  (stream-map * s1 s2))

(define factorials
  (cons-stream 1
               (mul-streams (stream-cdr integers)
                            factorials)))

(display-line (stream-head factorials 10))

练习 3.55

定义partial-sums实现流：\(S_0\)，\(S_0+S_1\)，\(S_0+S_1+S_2\)，\(S_0+S_1+S_2+S_3\)、 \(\cdots\)。例如(partical-sums integers)生成的是：\(1,3,6,10,15,\cdots\)。

使用练习 3.54 的方法，分析(partial-sums s)流，并找出隐藏在其中的流规律：

(partial-sums s)                x                           y

s0                                                          s0
s0 + s1                         s0                          s1
s0 + s1 + s2                    s0 + s1                     s2
s0 + s1 + s2 + s3               s0 + s1 + s2                s3
s0 + s1 + s2 + s3 + s4          s0 + s1 + s2 + s3           s4
s0 + s1 + s2 + s3 + s4 + s5     s0 + s1 + s2 + s3 +s 4      s5
...                             ...                         ...

分析的结果表明，(partial-sums s)可以表示为两个流之和： x流为(partial-sums s)本身，y流则是流s：

;;; 55-partial-sums.scm

(load "p228-add-streams.scm")

(define (partial-sums s)
    (cons-stream (stream-car s)
                 (add-streams (partial-sums s)
                              (stream-cdr s))))

(load "55-partial-sums.scm")
(load "p228-integers.scm")
(stream-head (partial-sums integers) 10)

add-streams时重新计算一个(partial-sums s)太浪费了， 于是我内部定义了一个self来递归：

(define (partial-sums stream)
  (define self
    (cons-stream (stream-car stream)
                 (add-streams self
                              (stream-cdr stream))))
  self)

练习 3.56

要求按递增的顺序不断枚举出符合每件的整数，要求是没有除了2，3，5以外的素数因子。

把这个流称为S，则：

• S从1开始。
• (scale-stream S 2)的元素也是S的元素。
• 这一说法对(scala-stream S 3)和(scale-stream S 5)也成立。
• 这些也是S的所有元素了。

现在骔一个过程merge把这些元素组合起来，它合并流并删除重复的元素：

(define (merge s1 s2)
  (cond ((stream-null? s1) s2)
        ((stream-null? s2) s1)
        (else
         (let ((s1car (stream-car s1))
               (s2car (stream-car s2)))
           (cond ((< s1car s2car)
                  (cons-stream s1car (merge (stream-cdr s1) s2)))
                 ((> s1car s2car)
                  (cons-stream s2car (merge s1 (stream-cdr s2))))
                 (else
                  (cons-stream s1car
                               (merge (stream-cdr s1)
                                      (stream-cdr s2)))))))))

然后就可以构造出所需要的流了：

(define S (cons-stream 1 (merge <??> <??>)))

请填写空白的部分。

(define s (cons-stream 1 
                       (merge (scale-stream s 2)
                              (merge (scale-stream s 3)
                                     (scale-stream s 5)))))

(stream-head s 10)     ;Value 13: (1 2 3 4 5 6 8 9 10 12)
(stream-head s 100)    ;Value 14: (1 2 3 4 5 6 8 9 10 12 15 16 .....

练习 3.57

1. 使用add-streams实现的fib过程在计算第n个数的时候要执行多少次加法？
2. 如果用(lambda () <exp>来实现(delay <exp>)，又不用memo-proc优化， 那么对加法的调用会指数级增加，请证明这一点。

从书本 227 页的 fibs 定义以及 229 页的 fibs 图示分析可知，对于第 i 个斐波那契数 ，也即是(stream-ref fibs i)，需要对(stream-ref fibs (- i 1))和 (stream-ref fibs (- i 2))进行一次加法。

对于使用记忆过程实现的，无重复的 fibs 来说， 每个(stream-ref fibs i)只需要被计算一次，以后就可以根据记忆过程来直接返回 计算结果。

因此，计算(stream-ref fibs n)总共需要 n 次加法，它产生的计算序列和书本 26 页的迭代版本的 fib 过程是一样的。

另一方面，如果使用不带记忆过程的 lambda 来实现 delay ， 那么对于每个(stream-ref fibs i)，都要对(stream-ref fibs (- i 1))和 (stream-ref fibs (- i 2))进行一次加法， 而对(stream-ref fibs (- i 1))的求值又引发(stream-ref fibs (-i 2)和 (stream-ref fibs (- i 3))进行相加，以此类推，一直回溯到 0 和 1 为止， 这一计算所产生的加法序列和书本 24 页指数级复杂度的递归 fib 过程产生的加法序列 一样，因此这一实现所需的加法将指数倍地上升。

练习 3.58

quotient过程是求两个整数的整数商。解释下面的流计算过程：

(define (expand num den radix)
  (cons-stream
   (quotient (* num radix) den)
   (expand (remainder (* num radix) den) den radix)))

• (expand 1 7 10)的结果
• expand 3 8 10的结果

从定义来看， expand 每次生成(* num radix)除以den的商， 然后将(* num radix)除以den的余数作为num参数，递归地调用expand：

;;; 58-expand.scm

(define (expand num den radix)
    (cons-stream
        (quotient (* num radix) den)
        (expand (remainder (* num radix) den) den radix)))

测试：

1 ]=> (load "58-expand.scm")

1 ]=> (stream-head (expand 1 7 10) 20)
;Value 13: (1 4 2 8 5 7 1 4 2 8 5 7 1 4 2 8 5 7 1 4)

1 ]=> (stream-head (expand 3 8 10) 20)
;Value 14: (3 7 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0)

quotient 返回两个除数之商，而 remainder 返沪两个除数之余：

1 ]=> (quotient 10 3)    ;Value: 3 
1 ]=> (remainder 10 3)   ;Value: 1

练习 3.59

用类似2.5.3节里处理多项式的方法来处理幂级数。比如，把：

\[ \begin{equation} \begin{split} e^x & = 1 + x + \frac{x^2}{2} + \frac{x^3}{3 \times 2} + \frac{x^4}{4 \times 3 \times 2} + \cdots \\ \cos x & = 1 - \frac{x^2}{2} + \frac{x^4}{4 \times 3 \times 2} - \cdots \\ \sin x & = x - \frac{x^3}{3 \times 2} + \frac{x^5}{5 \times 4 \times 3 \times 2} - \cdots \end{split} \end{equation} \]

表示为无穷的流：

• \(a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots\)表示为流。
• 流的元素就是\(a_0, a_1, a_2, a_3, \cdots\)

a) 级数\(a_0 + a_1x + a_2x^2 + a_3x^3 + \cdots\)的积分是级数：

\[ \begin{equation} \begin{split} c + a_0x + \frac{1}{2}a_1x^2 + \frac{1}{3}a_2x^3 + \frac{1}{4}a_3x^4 + \cdots \end{split} \end{equation} \]

这里的\(C\)表示任意常量。请定义intergrate-series：

• 它的参数是表示幂级数的流\(a_0, a_1, a_2, a_3, \cdots\)。
• 它的结果是积分中每个项的系数流 \(a_0, \frac{1}{2}a_1, \frac{1}{3}a_2, \frac{1}{4}a_3, \cdots\)。
• 因为返回的结果不包含常数项，所以它不是幂级数。如果要对它们使用 intergrage-series可以用cons加上一个常数项。

解一：

实现\(\frac{1}{1}, \frac{1}{2}, \cdots\)：

(define (div-streams s1 s2)
    (stream-map / s1 s2))

流的每个元素\(\frac{1}{i}a_{i-1}\)可以用mul-streams得出：

(define (mul-streams s1 s2)
    (stream-map * s1 s2))

结果为：

(define (integrate-series a)
    (mul-streams a                                  ; a0, a1, a2, ...
                 (div-streams ones integers)))      ; 1/1, 1/2, 1/3, ...

解二：

(define (integrate-series s)
  (stream-map * (stream-map / ones integers) s))

b)

• 函数\(x \mapsto e^x\)是其自身的导数，所以\(e^x\)和\(e^x\)的积分是同一个级数 （除了常数项外）。
• 而常数项应该是\(e^0=1\)。

所以，可以按以下方式生成\(e^x\)的级数：

(define exp-series
  (cons-stream 1 (integrate-series exp-series)))

已经知道sin的导数是cos，而cos的层数是负sin。所以如何生成sin和cos的级数：

(define cosine-series (cons-stream 1 <??>))

(define sine-series (cons-stream 0 <??>))

答：

(define sine-series 
  (cons-stream 0 (integrate-series cosine-series)))

(define cosine-series 
  (cons-stream 1 (integrate-series (scale-stream sine-series -1))))

练习 3.60

练习 3.59完成把幂级数表示为系数流以后，级数就可以直接用过程add-stream实现了， 请完成以下定义：

(define (mul-series s1 s2)
  (cons-stream <??> (add-streams <??> <??>)))

并用\(\sin^2x+\cos^2x=1\)来检验。

(include "3.5.2.scm")
(include "3-59.scm")

; s1 = (a + b) => a = (car s1), b = (cdr s1)
; s2 = (x + y) => x = (car s2), y = (cdr s2)
; s1 * s2 = a*x + b*x + (a+b)*y

(define (mul-series s1 s2)
    (cons-stream (* (stream-car s1) (stream-car s2))
                 (add-streams
                     (scale-stream (stream-cdr s1) (stream-car s2)) 
                     (mul-series s1 (stream-cdr s2)))))

test codes, commented out for 3-61

(display-line (stream-head 
    (mul-series sine-series sine-series) 10))

(display-line (stream-head 
    (mul-series cosine-series cosine-series) 10))

(define (x-stream x)
    (define self
        (cons-stream
            1
            (scale-stream self x)))
    self)

(display-line (stream-head (x-stream 2) 10))

(define xs (x-stream 2))

(define one (add-streams
                (stream-map * xs (mul-series sine-series sine-series))
                (stream-map * xs (mul-series cosine-series cosine-series))))

(display-line (stream-head one 10))

(include "gfelix.scm")

(display-line (fold-right + 0 (stream-head one 10)))

练习 3.61

令\(S\)是一个常数项为1的幂级数（练习3.59），假设要找出\(1/S\)的幂级数，也就是说， 找出一个级数\(X\)使得\(S \times X = 1\)。把\(S\)写成\(S = 1 + S_R\)，其中\(S_R\)是\(S\) 常数项后面的部分。然后就可以按下面的方式解出\(X\)：

\[ \begin{equation} \begin{split} S \times X &= 1 \\ (1 + S_R) \times X &= 1 \\ X + S_R \times X &= 1 \\ X &= 1 - S_R \times X \end{split} \end{equation} \]

综上所述，\(X\)是这样一个幂级数：

• 常数项为1；
• 其高阶的那些项可以由\(S_R\)求负后乘以\(X\)而得到。

请结合练习3.60的mul-series实现过程，使它能对常数项为1的幂级数\(S\)计算出\(1/S\)。

(include "3-60.scm")

(define (inverse-series s)
    (let ((minus-Sr (scale-stream (stream-cdr s) -1)))
        (define X
            (cons-stream
                1
                (mul-series minus-Sr X)))
        X))

;; test codes, commented out for 3-62

(define icosine-series (inverse-series cosine-series))
(display-line (stream-head cosine-series 10))
(display-line (stream-head icosine-series 10))

(include "gfelix.scm")

(display-line
    (exact->inexact
        (fold-right + 0
            (stream-head (mul-series cosine-series icosine-series) 5))))

练习 3.62

结合练习 3.61和3.62，定义过程div-series，完成两个幂级数的除法。 对于任何两个级数只要作为分母的级数具有非0的常数项（如果为0应该报错）。 如何利用div-series和练习3.59的结果产生出正切函数的幂级数。

(include "3-61.scm")

(define (div-series s1 s2)
    (let ((c (stream-car s2)))
        (if (= 0 c)
            (error "first item of s2 should not be zero -- DIV-SERIES" c)
            (scale-stream
                (mul-series
                    s1
                    (inverse-series (scale-stream s2 (/ 1 c))))
                (/ 1 c)))))

;; tan = sin/cos
(define tan-series (div-series sine-series cosine-series))

;; test code

(include "gfelix.scm")

(define (x-stream x)
    (define self
        (cons-stream
            1
            (scale-stream self x)))
    self)

(display-line
    (exact->inexact
        (fold-right + 0
            (stream-head (stream-map * tan-series (x-stream 0.8)) 30))))
; output:    1.0296385556333

; tan(0.8) = 1.0296385570503640127463611728204

流计算模式的使用

系统地将迭代操作方式表示为流过程

状态可以表示为值的「没有时间的」流，而不是视为一组不断更新的变量。

以求平方根为例，之前介绍过反复猜测的过程：

(define (sqrt-improve guess x)
  (average guess (/ x guess)))

换一个方式，以从1开始的流来表示：

(define (sqrt-stream x)
  (define guesses
    (cons-stream 1.0
                 (stream-map (lambda (guess)
                               (sqrt-improve guess x))
                             guesses)))
  guesses)

这样得到越来越多的项，不断得到更加接近的值：

(display-stream (sqrt-stream 2))
1.
1.5
1.4166666666666665
1.4142156862745097
1.4142135623746899
...

另一个例子可以迭代生成接近\(\pi\)的值：

\[ \begin{equation} \begin{split} \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \end{split} \end{equation} \]

实现过程：

(define (pi-summands n)
  (cons-stream (/ 1.0 n)
               (stream-map - (pi-summands (+ n 2)))))
(define pi-stream
  (scale-stream (partial-sums (pi-summands 1)) 4))

缺点是收敛的结果非常慢：

(display-stream pi-stream)
4.
2.666666666666667
3.466666666666667
2.8952380952380956
3.3396825396825403
2.9760461760461765
3.2837384837384844
3.017071817071818
...

欧拉实现过一个加速器对于交错符号的级数特别有效。假设\(S_n\)是原有序列的第\(n\)项， 那么加速序列的形式就是：

\[ \begin{equation} \begin{split} S_{n+1} - \frac{(S_{n+1}-S_n)^2}{S_{n-1}-2S_n+S_{n+1}} \end{split} \end{equation} \]

把变换应用到原来的值流上，程序表示为：

(define (euler-transform s)
  (let ((s0 (stream-ref s 0))           ; Sn-1
        (s1 (stream-ref s 1))           ; Sn
        (s2 (stream-ref s 2)))          ; Sn+1
    (cons-stream (- s2 (/ (square (- s2 s1))
                          (+ s0 (* -2 s1) s2)))
                 (euler-transform (stream-cdr s)))))

加速以后的效果收敛更快：

(display-stream (euler-transform pi-stream))
3.166666666666667
3.1333333333333337
3.1452380952380956
3.13968253968254
3.1427128427128435
3.1408813408813416
3.142071817071818
3.1412548236077655
...

加速器还可以加速另一个加速器，或者递归地加速下去。可以构造一个流的流， 其中的每个流都是前一个流的变换结果：

(define (make-tableau transform s)
  (cons-stream s
               (make-tableau transform
                             (transform s))))

这样得到以下这种被称为「表列」数据结构的结果：

\[ \begin{equation} \begin{split} S_{00} \quad & S_{01} \quad & S_{02} \quad & S_{03} \quad & S_{04} \quad & \cdots \\ \quad & S_{10} \quad & S_{11} \quad & S_{12} \quad & S_{13} \quad & \cdots \\ \quad & \quad & S_{20} \quad & S_{21} \quad & S_{22} \quad & \cdots \\ \quad & \quad & \quad & \quad & \cdots \quad & \end{split} \end{equation} \]

最后取出表列中每行的第一项，这样就可以形成一个序列：

(define (accelerated-sequence transform s)
  (stream-map stream-car
              (make-tableau transform s)))

这样只要8项就可以得到\(\pi\)中的14位数字：

(display-stream (accelerated-sequence euler-transform
                                      pi-stream))
4.
3.166666666666667
3.142105263157895
3.141599357319005
3.1415927140337785
3.1415926539752927
3.1415926535911765
3.141592653589778
...

练习 3.63

如果直接用(lambda () <exp>)实现delay，而不用memo-proc提供的优化，如上：

(define (sqrt-stream x)
  (cons-stream 1.0
               (stream-map (lambda (guess)
                             (sqrt-improve guess x))
                           (sqrt-stream x))))

性能上会有哪些差异：

这个版本的sqrt-stream计算第\(i\)个元素的时候，要递归地计算以第\(i-1\)个元素开头的 stream，导致效率过低。使用原先版本的sqrt-stream可以则始终依赖于同一个stream， 由于有记忆过程，所以效率是\(\Theta(n)\)的。

练习 3.64

实现stream-limit，参数为一个流和一个表示可接受误差的数值。不断检查流直到 两项之间的差超过误差，这时返回最后一项。用下面方式计算出满足给定误差的平方根：

(define (sqrt x tolerance)
  (stream-limit (sqrt-stream x) tolerance))

解：

;;; 64-stream-limit.scm

(define (stream-limit stream tolerance)
    (let ((ref-n (stream-car stream))
          (ref-n+1 (stream-car (stream-cdr stream))))
        (if (close-enough? ref-n ref-n+1 tolerance)
            ref-n+1
            (stream-limit (stream-cdr stream) tolerance))))

(define (close-enough? x y tolerance)
    (< (abs (- x y))
       tolerance))

sqrt载入stream-limit，以及书本232页、233页定义的sqrt-stream：

;;; 64-sqrt.scm

(load "64-stream-limit.scm")
(load "p233-sqrt-stream.scm")

(define (sqrt x tolerance)
    (stream-limit (sqrt-stream x) tolerance))


(load "64-sqrt.scm")

(sqrt 9 0.0001)                  ;Value: 3.000000001396984

练习 3.65

用以下级数计算出逼近2的自然对数的三个序列，并评估收敛速度：

\[ \begin{equation} \begin{split} ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots \end{split} \end{equation} \]

以下是\(ln 2\)的流定义：

;;; 65-ln2.scm

(load "55-partial-sums.scm")

(define (ln2-stream n)
    (cons-stream (/ 1.0 n)
                 (stream-map - (ln2-stream (+ n 1)))))

(define ln2
    (partial-sums (ln2-stream 1)))

它的前 10 个项如下：

(load "65-ln2.scm")

(stream-head ln2 10)
;Value 12: (1. .5 .8333333333333333 .5833333333333333 .7833333333333332 
		.6166666666666666 .7595238095238095 .6345238095238095 .7456349206349207 
		.6456349206349207)

可以用书本 234 页介绍的欧拉加速器来加快它的收敛：

(load "p234-euler-transform.scm")

(stream-head (euler-transform ln2) 10)
;Value 11: (.7 .6904761904761905 .6944444444444444 .6924242424242424 
		.6935897435897436 .6928571428571428 .6933473389355742 .6930033416875522 
		.6932539682539683 .6930657506744464)

还可以使用超级加速器，再次加速：

(load "p234-accelerated-sequence.scm")

(stream-head (accelerated-sequence euler-transform ln2) 9)

;Value 14: (1. .7 .6932773109243697 .6931488693329254 .6931471960735491 
		.6931471806635636 .6931471805604039 .6931471805599445 .6931471805599427)

可以看出，使用超级加速器的效果非常显著，只使用 9 个猜测就逼近到了\(ln 2\)的后 14 位\(0.69314718055994\)。

Note

测试中只取出了超级加速器的前 9 项，因为再猜测下去会出错， 可能是因为计算所需的精度超过了 MIT Scheme 的浮点精度：

1 ]=> (stream-head (accelerated-sequence euler-transform ln2) 10)

;Invalid floating-point operation
;To continue, call RESTART with an option number:
; (RESTART 1) => Return to read-eval-print level 1.

See also

ln2 的准确值可以从 http://oeis.org/A002162 查看。

序对的无穷流

以2.2.3节的prime-sum-pairs过例子，它的要求是生成满足条件的(i, j)的流， 要满足条件：

1. \(i \leq j\)
2. \(i+j\)为素数

以上需求可以表示为：

(stream-filter (lambda (pair)
                 (prime? (+ (car pair) (cadr pair))))
               int-pairs)

其中过滤器实现了\(i+j\)为素数的要求， 剩下的问题就是如何生成满足\(i \leq j\)整数序对的流int-pairs。

首先先来看简单的情况，两个流\(S=(S_i)\)和\(T=(T_j)\)，可以表示为无穷的矩阵：

\[ \begin{equation} \begin{split} (S_0, T_0) \quad & (S_0, T_1) \quad & (S_0, T_2) \quad & \cdots \\ (S_1, T_0) \quad & (S_1, T_1) \quad & (S_1, T_2) \quad & \cdots \\ (S_2, T_0) \quad & (S_2, T_1) \quad & (S_2, T_2) \quad & \cdots \\ \cdots \quad & \end{split} \end{equation} \]

在这个基础上过滤出对角线上方的部分就是int-pairs，在这里称它为(pairs S T)：

\[ \begin{equation} \begin{split} (S_0, T_0) \quad & (S_0, T_1) \quad & (S_0, T_2) \quad & \cdots \\ \quad & (S_1, T_1) \quad & (S_1, T_2) \quad & \cdots \\ \quad & \quad & (S_2, T_2) \quad & \cdots \\ \quad & \quad & \quad & \cdots \quad & \end{split} \end{equation} \]

这半个矩阵可以分为三部分处理：

1. 第一行第一个元素
2. 第一行的其他元素
3. 其他所有元素

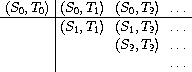
其中第三部分正好可以递归地表示为(stream-cdr S)和(stream-cdr T)组成的序对。

而第二部分就是：

(stream-map (lambda (x) (list (stream-car s) x))
            (stream-cdr t))

现在可以大致确定用以下方法构成序对流：

(define (pairs s t)
  (cons-stream
   (list (stream-car s) (stream-car t))
   (<combine-in-some-way>                                 ;; 按某种方法组成
       (stream-map (lambda (x) (list (stream-car s) x))
                   (stream-cdr t))
       (pairs (stream-cdr s) (stream-cdr t)))))

接下来要实现如何组合两个内部流，但问题是类似2.2.1节的append过程在这里不适用：

(define (stream-append s1 s2)
  (if (stream-null? s1)
      s2
      (cons-stream (stream-car s1)
                   (stream-append (stream-cdr s1) s2))))

因为它要在取得第一个流的所有元素后再结合第二个流，而这里的两个流都是无穷的。 所以需要改为使用交替执行的方式，比如以下的interleave：

(define (interleave s1 s2)
  (if (stream-null? s1)
      s2
      (cons-stream (stream-car s1)
                   (interleave s2 (stream-cdr s1)))))

现在可以填上pairs程序中的空白：

(define (pairs s t)
  (cons-stream
    (list (stream-car s) (stream-car t))
    (interleave
      (stream-map (lambda (x) (list (stream-car s) x))
                  (stream-cdr t))
      (pairs (stream-cdr s) (stream-cdr t)))))

练习 3.66

练习 3.67

修改pairs，新的程序不考虑条件\(i \leq j\)。（提示：需要混入另一个流）

(include "3.5.3-pairs.scm")

(define (pair-all s t)
  (cons-stream
    (list (stream-car s) (stream-car t))
    (interleave-streams
      (stream-map
        (lambda (x) (list (stream-car s) x))
        (stream-cdr t))
      (stream-map
        (lambda (x) (list (stream-car t) x))
        (stream-cdr s))
      (pair-all (stream-cdr s) (stream-cdr t)))))

(display (stream-head (pair-all nature-number-stream nature-number-stream) 20))

练习 3.68

如果不把半个矩阵分为三个部分，把\((S_0, T_0)\)与第一行其他部分作为整体， 用以下的方式直接处理是否可行：

(define (pairs s t)
  (interleave
   (stream-map (lambda (x) (list (stream-car s) x))
               t)
   (pairs (stream-cdr s) (stream-cdr t))))

由于interleave不是一个语法结构，会导致pairs不断递归调用自己，最终爆栈。

练习 3.69

实现过程triples，参数为三个无穷流S、T和U，生成三元组\((S_i, T_j, U_k)\) 的流，其中\(i \leq j \leq k\)。

然后再利用triples生成所有毕达哥拉斯三元组的流\((i, j, k)\)，其中\(i \leq j\)， 而且\(i^2 + j^2 = k^2\)。

(include "3.5.3-pairs.scm")

(define (triples s t u)
    (let ((s0 (stream-car s))
          (t0 (stream-car t))
          (u0 (stream-car u))
          (s+ (stream-cdr s))
          (t+ (stream-cdr t))
          (u+ (stream-cdr u)))
     (cons-stream
        (list s0 t0 u0)
        (interleave
            (stream-map
                (lambda (tu) (cons s0 tu)) (stream-cdr (pairs t u)))
            (triples s+ t+ u+)))))

;(display (stream-head (triples integers integers integers) 100))

(define (ok? i j k)
  (= (+ (* i i) (* j j)) (* k k)))

(define Pythagoras-triples
    (stream-filter
        (lambda (stu) (apply ok? stu))
        (triples integers integers integers)))

(display (stream-head Pythagoras-triples 4))

练习 3.70 无穷流中的序对排序

定义排序的权重函数\(W(i,j)\)，如果\(W(i_1,j_1) \lt W(i_2,j_2)\)就代表 \((i_1,j_1) \lt (i_2,j_2)\)。

• 参考merge实现merge-weighted，它以weight计算权重。
• 再把pairs过程改进为weighted-pairs照指定权重顺序生成序对的流。

最终生成：

1. 所有正整数序对\((i,j)\)的流，要求\(i \leq j\)并按\(i + j\)排序。
2. 所有正整数序对\((i,j)\)的流，要求\(i\)与\(j\)可以被2、3或5整除， 并按\(2i+3j+5ij\)排序。

(include "3.5.3-pairs.scm")

(define (weighted-merge weighter s t)
    (if (stream-null? s)
        t
        (let ((ws (weighter (stream-car s)))
              (wt (weighter (stream-car t))))
            (if (< ws wt)
                (cons-stream
                    (stream-car s)
                    (weighted-merge weighter (stream-cdr s) t))
                (cons-stream
                    (stream-car t)
                    (weighted-merge weighter (stream-cdr t) s))))))

(define (weighted-pairs weighter s t)
    (cons-stream
        (list (stream-car s) (stream-car t))
        (weighted-merge
            weighter
            (stream-map (lambda (x) (list (stream-car s) x)) (stream-cdr t))
            (weighted-pairs weighter (stream-cdr s) (stream-cdr t)))))

(define (weighter-a pair)
    (apply + pair))

;(display-line (stream-head (weighted-pairs weighter-a integers integers) 10))

(define (weighter-b pair)
    (let ((i (car pair))
          (j (cadr pair)))
        (+ (* 2 i) (* 3 j) (* 5 i j))))

; 2/3/5的倍数什么的有点莫名其妙，这里就忽略了吧。。。

;(display (stream-head (weighted-pairs weighter-b integers integers) 10))

练习 3.71

可以用多种方式表示为两个数的立方和（\(i^3+j^3\)）的数被称为Ramanujan数。 以\(i^3+j^3\)作为权重生成Ramanujan序对流，比如第一个是1729，求以后的5个数：

(include "3-70.scm")

(define (weight-R pair)
    (apply + (map (lambda (x) (* x x x)) pair)))

(define p (weighted-pairs weight-R integers integers))

#|
(define (find-next stream weight)
    (let ((w (weight-R (stream-car stream))))
        (if (= weight w)
            (cons-stream
                w
                (find-next (stream-cdr stream) w))
            (find-next (stream-cdr stream) w))))

(define Ramanujan (find-next p 0))
|#

(define (find-next stream)
    (let ((s0 (stream-ref stream 0))
          (s1 (stream-ref stream 1)))
        (if (= (weight-R s0) (weight-R s1))
            (cons-stream
                (list (weight-R s0) s0 s1)
                (find-next 
                    (stream-cdr (stream-cdr stream))))
            (find-next (stream-cdr stream)))))

(define Ramanujan (find-next p))

(display-line (stream-head Ramanujan 10))

练习 3.72

类似练习3.72，生成能以三种以上方式表示为两个数平方和的整数流，并显示分解方式。

(include "3-70.scm")

(define (weight-square pair)
    (apply + (map (lambda (x) (* x x)) pair)))

(define p (weighted-pairs weight-square integers integers))

(define (find-next stream)
    (let ((s0 (stream-ref stream 0))
          (s1 (stream-ref stream 1))
          (s2 (stream-ref stream 2)))
        (if (= (weight-square s0) (weight-square s1) (weight-square s2))
            (cons-stream
                (list (weight-square s0) s0 s1 s2)
                (find-next 
                    (stream-cdr (stream-cdr (stream-cdr stream)))))
            (find-next (stream-cdr stream)))))

(display-line (stream-head (find-next p) 10))

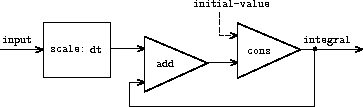
将流作为信号

用流里的元素表示信号在顺序时间间隔上的值。例如用「积分器」或是「求和器」， 对于输入流\(x = (x_i)\)，初始值\(C\)和一个小增量\(dt\)，累积下面的和：

\[ \begin{equation} \begin{split} S_i = C + \sum_{j=1}^{i}x_j {\rm d}t \end{split} \end{equation} \]

返回的流就是\(S=(S_i)\)。程序实现类似3.5.2节中「隐式风格」的整数流：

(define (integral integrand initial-value dt)
  (define int
    (cons-stream initial-value
                 (add-streams (scale-stream integrand dt)
                              int)))
  int)

练习 3.73

有一个RC电路，由一个阻值为\(R\)的电阻和一个容量为\(C\)的电容串连。 它对于输入电流\(i\)的电压响应\(v\)如下公式表示：

\[ \begin{equation} \begin{split} v = v_0 + \frac{1}{C}\int^{t}_{0}i{\rm d}t + R_i \end{split} \end{equation} \]

结构与对应的信号流图发下：

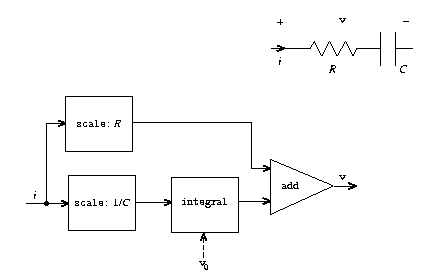
要求实现一个过程RC模拟这个电路：

• 输入为\(R\)、\(C\)和\({\rm d}t\)作为输入。
• 返回值为过程：
  • 输入为为表示电流的流\(i\)和表示初始电压值的\(v_0\)。
  • 输出的表示电压的流\(v\)。

例如，能够通过求值：

(define RC1 (RC 5 1 0.5))

得到一个模拟电路RC1其中：

• \(R\)等于5欧姆
• \(C\)等于1法
• 时间步长为0.5秒

(include "3.5.3-signal.scm")

(define (RC R C dt)
    (lambda (i v0)
        (add-streams
            (integral (scale-stream i (/ 1 C)) v0 dt)
            (scale-stream i R))))

练习 3.74

要求实现过程sig-change-detector，输入信号流sense-data， 输出信号流为zero-crossings在输入信号从负变正表示+1，从正变负表示-1， 其他为0。实现代码如下：

(define (make-zero-crossings input-stream last-value)
  (cons-stream
   (sign-change-detector (stream-car input-stream) last-value)
   (make-zero-crossings (stream-cdr input-stream)
                        (stream-car input-stream))))

(define zero-crossings (make-zero-crossings sense-data 0))

更新版本可以，模拟stream-map风格的程序，填写以下过程的空白：

(define zero-crossings
  (stream-map sign-change-detector sense-data <expression>))

答：

(include "3.5.3-pairs.scm")

(define sense-data 
  (list->stream '(1 2 1.5 1 0.5 -0.1 -2 -3 -2 -0.5 0.2 3 4 0 0 0)))

(define (sign-change-detector now last)
    (cond
        ((and (< last 0) (> now 0)) 1)
        ((and (> last 0) (< now 0)) -1)
        (else 0)))

#|
(define (make-zero-crossings input-stream last-value)
    (cons-stream
        (sign-change-detector (stream-car input-stream) last-value)
        (make-zero-crossings
            (stream-cdr input-stream)
            (stream-car input-stream))))

(define zero-crossings (make-zero-crossings sense-data 0))

;(display-line (stream-head zero-crossings 13))
|#

(define zero-crossings
    (stream-map sign-change-detector sense-data
        (cons-stream 0 sense-data)))

;(display-line (stream-head zero-crossings 13))

练习 3.75

改进练习 3.74中的程序，增加过滤噪音的功能。对信号做平滑，在提取过零点前过滤噪音 。方案是对每个输入信号与前一个信号作平均值：

(define (make-zero-crossings input-stream last-value)
  (let ((avpt (/ (+ (stream-car input-stream) last-value) 2)))
    (cons-stream (sign-change-detector avpt last-value)
                 (make-zero-crossings (stream-cdr input-stream)
                                      avpt))))

但以上的程序有错误（需要增加make-zero-crossings的参数个数）：

(include "3-74.scm")

(define (make-zero-crossings input-stream last-value last-avpt)
    (let ((avpt (/ (+ (stream-car input-stream) last-value) 2)))
        (cons-stream
            (sign-change-detector avpt last-avpt)
            (make-zero-crossings
                (stream-cdr input-stream)
                (stream-car input-stream)
                avpt))))
    
(define zero-crossings (make-zero-crossings sense-data 0 0))

(display-line (stream-head zero-crossings 13))

练习 3.76

让练习 3.76的程序更加模块化，把平滑信号的逻辑抽象为smooth过程：

(include "3-74.scm")

(define (smooth stream)
    (stream-map
        (lambda (a b) (/ (+ a b) 2))
        stream
        (stream-cdr stream)))

(define smoothed-sense-data (smooth sense-data))

(define zero-crossings
    (stream-map
        sign-change-detector
        smoothed-sense-data
        (cons-stream 0 smoothed-sense-data)))

(display-line (stream-head zero-crossings 13))

流和延时求值

延时流的实现依赖于cons-stream操作带有delay特性。比如：

(define int
  (cons-stream initial-value
               (add-streams (scale-stream integrand dt)  ;; delay
                            int)))

以上代码的add-streams部分不会被执行，因为它是cons-stream的第二个参数。

但是对于「带有循环的系统」的流模拟，光靠cons-stream的延时求值特性可能不够， 还要显式地使用delay操作。例如求解微分方程的信号处理系统：

\[ \begin{equation} \begin{split} \frac{{\rm d}y}{{\rm d}t} = f(y) \end{split} \end{equation} \]

对于一个给定的函数\(f\)，一个映射部件将函数\(f\)应用于其输入信号的情况， 它也连接在一个反馈循环里，循环中包含一个积分器， 连接方式和模拟计算机中实际用于求解这种方程的电路形式很相似：

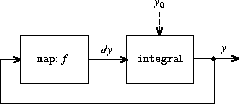
对于\(y\)的一个输入值\(y_0\)，实现方式为：

(define (solve f y0 dt)
  (define y (integral dy y0 dt))
  (define dy (stream-map f y))
  y)

这里问题在于define y里调用了dy，但是dy要到后面才定义。正确的方式为：

1. 在不求值积分对象dy的前题下输出流y里第一个元素。
2. 有了y的第一个元素，就可以执行stream-map，生成dy的第一个元素。
3. 这样就可以循环下去了……

为了实现这一特性，需要重新定义intergral，把被积的流视为一个「延时参数」。 integral将在需要生成输出流第一个元素之后的元素时froce积分对象的求值：

(define (integral delayed-integrand initial-value dt)
  (define int
    (cons-stream initial-value
                 (let ((integrand (force delayed-integrand)))
                   (add-streams (scale-stream integrand dt)
                                int))))
  int)

接下来只要在y的定义里延时求值dy，就可以实现solve过程了（各个 Scheme里实现方式不一样，详见4.1.6节）：

(define (solve f y0 dt)
  (define y (integral (delay dy) y0 dt))
  (define dy (stream-map f y))
  y)

执行演示了在\(y=1\)处，初始条件为\(y(0)=1\)的情况下，\(\frac{{\rm d}y}{{\rm d}t}=y\) 的解，近似值\(e \approx 2.718\)：

(stream-ref (solve (lambda (y) y) 1 0.001) 1000)   ;; 2.716924

练习 3.77

以下这个integral的形式类似于integers-starting-from。修改它让它也能用在 solve过程中：

(define (integral integrand initial-value dt)
  (cons-stream initial-value
               (if (stream-null? integrand)
                   the-empty-stream
                   (integral (stream-cdr integrand)
                             (+ (* dt (stream-car integrand))
                                initial-value)
                             dt))))

(include "3.5.4.scm")

#|
(define (integral integrand initial-value dt)
    (cons-stream initial-value
        (if (stream-null? integrand)
            the-empty-stream
            (integral (stream-cdr integrand)
                (+ (* dt (stream-car integrand)) initial-value)
                dt))))
|#

(define (integral delayed-integrand initial-value dt)
    (cons-stream initial-value
        (let ((integrand (force delayed-integrand)))
            (if (stream-null? integrand)
                the-empty-stream
                (integral (delay (stream-cdr integrand))
                    (+ (* dt (stream-car integrand)) initial-value)
                    dt)))))

(define (solve f y0 dt)
    (define y (integral (delay dy) y0 dt))
    (define dy (stream-map f y))
    y)

(display (stream-ref (solve (lambda (y) y) 1 0.001) 1000))

练习 3.78

对于齐次二阶线性微分方程：

\[ \begin{equation} \begin{split} \frac{{\rm d}^2y}{{\rm d}t^2} - a\frac{{\rm d}y}{{\rm d}t} - by =0 \end{split} \end{equation} \]

输出模拟流\(y\)由一个循环网络生成，因为：

1. \(\frac{{\rm d}^2y}{{\rm d}t^2}\)依赖于\(y\)和\(\frac{{\rm d}y}{{\rm d}t}\)；
2. 而\(y\)和\(\frac{{\rm d}y}{{\rm d}t}\)又被\(\frac{{\rm d}^2y}{{\rm d}t^2}\)确定；

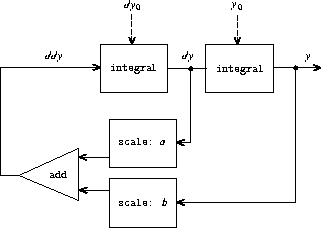
实现过程solve-2nd，以常数\(a\)、\(b\)和\({\rm d}t\)，\(y\)的初始值\(y0\)和\({\rm d}y_0\)， 和\(\frac{{\rm d}y}{{\rm d}t}\)为参数，生成\(y\)的流：

(include "3.5.4.scm")

(define (solve-2nd a b dt y0 dy0)
    (define y (integral (delay dy) y0 dt))
    (define dy (integral (delay ddy) dy0 dt))
    (define ddy (add-streams (scale-stream dy a) (scale-stream y b)))
    y)

练习 3.79

增加solve-2nd，让它能求解一般的二次微分方程：

\[ \begin{equation} \begin{split} \frac{{\rm d}^2y}{{\rm d}t^2} = f(\frac{{\rm d}y}{{\rm d}t}, y) \end{split} \end{equation} \]

(include "3.5.4.scm")

(define (solve-2nd f dt y0 dy0)
    (define y (integral (delay dy) y0 dt))
    (define dy (integral (delay ddy) dy0 dt))
    (define ddy (stream-map f dy y))
    y)

练习 3.80

串联RLC电路由以下部件组成：

1. 电阻量\(R\)
2. 电容量\(L\)
3. 电感量\(C\)

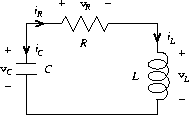
三个部件间电压\(v\)和电流\(i\)的关系为：

\[ \begin{equation} \begin{split} v_R &=i_RR \\ v_L &=L\frac{{\rm d}i_L}{{\rm d}t} \\ v_C &=C\frac{{\rm d}v_C}{{\rm d}t} \end{split} \end{equation} \]

电路连接导致以下的关系：

\[ \begin{equation} \begin{split} i_R &= i_L = -i_C \\ v_C &= v_L + v_R \end{split} \end{equation} \]

请结合以上方程证明电路的状态（\(v_C\)和\(i_L\)）可以由以下微分方程描述：

\[ \begin{equation} \begin{split} \frac{{\rm d}v_C}{{\rm d}t} &= \frac{i_L}{C} \\ \frac{{\rm d}i_L}{{\rm d}t} &= \frac{1}{L}v_C - \frac{R}{L}i_L \end{split} \end{equation} \]

信号流程图如下所示：

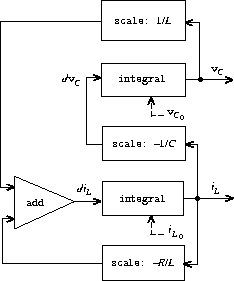
请实现过程RLC：

• 它的参数为\(R\)、\(L\)、\(C\)和时间增量\({\rm d}t\)。
• 返回值为过程：
  • 参数为状态变量的初始值\(V_{C_0}\)和\(i_{L_0}\)。
  • 返回值为\(v_C\)和\(i_L\)的序对。

然后利用RLC生成一对流，模拟RLC电路的行为，其中\(R\)为1欧,\(C\)为0.2法，\(L\)为1亨， \({\rm d}t\)为0.1秒，初始值\(V_{C_0}\)为10伏特，\(i_{L_0}\)为0安培。

(include "3.5.4.scm")

(define (RLC R L C dt)
    (lambda (vC0 iL0)
        (define vC (integral (delay dvC) vC0 dt))
        (define iL (integral (delay diL) iL0 dt))
        (define dvC (scale-stream iL (- (/ 1 C))))
        (define diL (add-streams (scale-stream vC (/ 1 L))
                                 (scale-stream iL (- (/ R L)))))
        (stream-map cons vC iL)))

(define xRLC ((RLC 1 1 0.2 0.1) 10 0))

(display  (stream-head xRLC 10))

规范求值序

对于增加了延时求值参数的过程，就要保证调用时传入的参数是延时实例。 这样的性质相当于把语言转到了正则序的过程代换模型（而Scheme本身是应用序）。

数据的变动性和延时求值这二者结合得不是很好，延时求值对依赖于事件顺序的程序能力 造成很大的影响，例如：赋值、变动数据、执行输入输出。

「函数式程序的模块化」与「对象的模块化」

• 引入赋值操作是为了实现模块化，因为局部变量可以把状态隐藏在内部。
• 流模型不但可以提供等价的模块化，而且不用进行赋值操作。

用流来改写3.1.2节用蒙特卡罗估计方法。首先是随机数生成器：

(define rand
  (let ((x random-init))
    (lambda ()
      (set! x (rand-update x))
      x)))

在流的形式中根本不存在随机数生成器，只有一个随机数流，通过rand-update 不断生成新的随机数：

(define random-numbers
  (cons-stream random-init
               (stream-map rand-update random-numbers)))

然后用它构造出random-numbers流，在流中顺序的数对上试验输出流：

(define cesaro-stream
  (map-successive-pairs (lambda (r1 r2) (= (gcd r1 r2) 1))
                        random-numbers))

(define (map-successive-pairs f s)
  (cons-stream
   (f (stream-car s) (stream-car (stream-cdr s)))
   (map-successive-pairs f (stream-cdr (stream-cdr s)))))

cesaro-stream馈入monte-carlo过程，monte-carlo双生成一个可能性估计的流。 结果被变换到一个估计\(\pi\)值的流。这里不需要用参数去告诉它被调用了多少次，

(define (monte-carlo experiment-stream passed failed)
  (define (next passed failed)
    (cons-stream
     (/ passed (+ passed failed))
     (monte-carlo
      (stream-cdr experiment-stream) passed failed)))
  (if (stream-car experiment-stream)
      (next (+ passed 1) failed)
      (next passed (+ failed 1))))

(define pi
  (stream-map (lambda (p) (sqrt (/ 6 p)))
              (monte-carlo cesaro-stream 0 0)))

练习 3.81

练习 3.6的随机数生成器可以被重置，强化随机数流，让它：

• 对一个表示需求的输入流操作。
• generate一个新的随机数
• reset为某个特定的值。

解：

action-stream should consists of symbol 'generate or number which means to reset random-init

(include "3.5.5.scm")

(define (rand-stream random-init action-stream)
  (define rand
    (cons-stream
      random-init
      (cond
        ((stream-null? action-stream) the-empty-stream)
        ((eq? 'generate (stream-car action-stream))
          (stream-map rand-update rand))
        (else
          (rand-stream (stream-car action-stream) 
                       (stream-cdr action-stream))))))
  rand)

练习 3.82

用流重写练习 3.5的蒙特卡罗积分，不需要参数传递执行试验的次数，而是生成一个表示 多次次数的估值流。

(include "3.5.5.scm")

(define rand-max 2147483648.0)

(define float-random-numbers
    (stream-map (lambda (x) (/ x rand-max)) random-numbers))

(define (estimate-integral p? x1 x2 y1 y2)
    (monte-carlo
        (map-successive-pairs 
            (lambda (x y)
                (let ((xx (+ (* x (- x2 x1)) x1))
                      (yy (+ (* y (- y2 y1)) y1)))
                    (p? xx yy)))
            float-random-numbers)
        0 0))

(define radius 0.5)
    
(define (in-circle-test x y)
  (<
    (+ (square (- x radius))
       (square (- y radius)))
    (square radius)))

(define pi-stream
    (stream-map
        (lambda (x) (/ x (square radius)))
        (estimate-integral in-circle-test 0.0 1.0 0.0 1.0)))

(display (stream-ref pi-stream 10000))

时间的函数程序设计观点

用流模拟变化的值，就可以把虚拟世界里的时间与求值过程中的执行顺序分解开来。

以3.1.3节里的提款程序为例：

• 构造函数以一个初始的余额balance构造实例。
• 根据每次调用时传入的参数amout，更新局部变量balance的不断变化。

(define (make-simplified-withdraw balance)
  (lambda (amount)
    (set! balance (- balance amount))
    balance))

而通过流来实现：

• 构造函数以一个「初始金额」和「每次提款金额流」构造实例。
• 通过「提款流」可以得到余额流。

(define (stream-withdraw balance amount-stream)
  (cons-stream
   balance
   (stream-withdraw (- balance (stream-car amount-stream))
                    (stream-cdr amount-stream))))

这样做的优点是更加符合良好的数学函数定义；而对用户来说却是一个交互操作的过程。

这样做也有缺点，比如有两个人Peter和Paul共用一个账户，那么可以把两个人的提款操作 合并成一个流：

但问题就麻烦在「合并」这个操作上：具体用什么方式来合并呢？

• 如果采用「轮流」的操作方式，两个人一个取一个操作，如果取款操作是阻塞式的， 那么一个人取款以后要等另一个人操作后才轮到自己。
• 而且取款的操作以流里的顺序也要和现实世界中取款的顺序一致， 不然就会因为并发问题而导致金额错误。

总的来说，本章介绍了两种计算模型：

• 一种方式是把世界模拟为相互分离、受时间约束的、有内部状态的对象。
• 一种方式是把世界模拟为单一的、无时间也无状态的统一体。
• 二者各有优势，便又都不完美。