ch04 元语言抽象 part04
逻辑程序设计
- 计算机科学处理的是命令式(怎么做)的知识。
- 数学处理的是说明式(是什么)的知识。
逻辑程序设计语言,一个表达式也可以解释为计算机该值的方法,如:SQL。 目前的逻辑程序设计语言都有一些缺陷:它们里面相关于「怎么做」的通用方法, 有可能陷入谬误性的无穷循环或其他非期望的行为之中。
本节要实现一种「查询语言」,它的求值器也有「求值部分」与「应用部分」, 还有实现语言的「抽象机制」(Lisp里是用过程实现抽象,逻辑语言里的规则)。 在这个实现中核心角色是一种栈帧数据结构,它确定了符号与它们的关联之间的对应。 并且在这个实现方案中用到了流。
演绎信息检索
一个实例数据库
实现一个公司的人事数据库,用断言表示一个信息。每个断言都是一个三个元素的表, 其中每个元素也可以是另一个表。例如:
(address (Bitdiddle Ben) (Slumerville (Ridge Road) 10)) ;; Ben的地址 (job (Bitdiddle Ben) (computer wizard)) ;; Ben的职务 (salary (Bitdiddle Ben) 60000) ;; Ben的薪水
Ben手有两个程序员和一个技师:
(address (Hacker Alyssa P) (Cambridge (Mass Ave) 78)) (job (Hacker Alyssa P) (computer programmer)) (salary (Hacker Alyssa P) 40000) (supervisor (Hacker Alyssa P) (Bitdiddle Ben)) ;; 上级领导是Ben (address (Fect Cy D) (Cambridge (Ames Street) 3)) (job (Fect Cy D) (computer programmer)) (salary (Fect Cy D) 35000) (supervisor (Fect Cy D) (Bitdiddle Ben)) ;; 上级领导是Ben (address (Tweakit Lem E) (Boston (Bay State Road) 22)) (job (Tweakit Lem E) (computer technician)) (salary (Tweakit Lem E) 25000) (supervisor (Tweakit Lem E) (Bitdiddle Ben)) ;; 上级领导是Ben
Alyssa指导的实习程序员:
(address (Reasoner Louis) (Slumerville (Pine Tree Road) 80)) (job (Reasoner Louis) (computer programmer trainee)) (salary (Reasoner Louis) 30000) (supervisor (Reasoner Louis) (Hacker Alyssa P))
注意以上job记录记录中,第三个元素的第一个子元素computer表示部门是电脑部。
Ben是高级员工,直接上司就是大老板本人:
(supervisor (Bitdiddle Ben) (Warbucks Oliver)) (address (Warbucks Oliver) (Swellesley (Top Heap Road))) (job (Warbucks Oliver) (administration big wheel)) (salary (Warbucks Oliver) 150000)
会计分总的相关信息:
(address (Scrooge Eben) (Weston (Shady Lane) 10)) (job (Scrooge Eben) (accounting chief accountant)) (salary (Scrooge Eben) 75000) (supervisor (Scrooge Eben) (Warbucks Oliver)) (address (Cratchet Robert) (Allston (N Harvard Street) 16)) (job (Cratchet Robert) (accounting scrivener)) (salary (Cratchet Robert) 18000) (supervisor (Cratchet Robert) (Scrooge Eben))
大老板的秘书:
(address (Aull DeWitt) (Slumerville (Onion Square) 5)) (job (Aull DeWitt) (administration secretary)) (salary (Aull DeWitt) 25000) (supervisor (Aull DeWitt) (Warbucks Oliver))
还有一些断言,描述有些人可以做别的工作。比如计算机大师可以代替程序员和技师:
(can-do-job (computer wizard) (computer programmer)) (can-do-job (computer wizard) (computer technician))
程序员可以代替实习程序员:
(can-do-job (computer programmer)
(computer programmer trainee))
大老板不在时,由秘书代大老板:
(can-do-job (administration secretary)
(administration big wheel))
简单查询
?变量名的形式可以匹配任何内容。如:
;;; Query input: (job ?x (computer programmer)) ;;; Query results: (job (Hacker Alyssa P) (computer programmer)) (job (Fect Cy D) (computer programmer)) (address ?x ?y) ;;; 查询多个变量 (supervisor ?x ?x) ;;; 同一个变量位于不同位置,找出上司就是自己
通过. ?变量名匹配多个元素:
(job ?x (computer ?type)) ;;; 只匹配一个元素 ;;; 匹配的结果 (job (Bitdiddle Ben) (computer wizard)) (job (Hacker Alyssa P) (computer programmer)) (job (Fect Cy D) (computer programmer)) (job (Tweakit Lem E) (computer technician))
(job ?x (computer . ?type)) ;;; 匹配多个元素的查询 ;;; 匹配的结果 (job (Reasoner Louis) (computer programmer trainee))
具体来说:
(computer . ?type) ;;; 能匹配 (computer programmer trainee) ;;; ?type的值是(programmer trainee) (computer programmer) ;;; ?type的值是(programmer) (computer) ;;; ?type的值是空表().
练习 4.55
写出查询语句:
- 所有被Ben Bitdiddle管理的人。
- 会计总所有人的名字和工作。
- 在Slumerville居住的所有人的名字和地址。
(supervisor ?person (Bitdiddle Ben)) (job ?person (accounting . ?work)) (address ?person (Slumerville . ?address))
复合查询
and操作的格式:
(and <query1> <query2> ... <queryn>)
(and (job ?person (computer programmer))
(address ?person ?where))
;;; 结果:
(and (job (Hacker Alyssa P) (computer programmer))
(address (Hacker Alyssa P) (Cambridge (Mass Ave) 78)))
(and (job (Fect Cy D) (computer programmer))
(address (Fect Cy D) (Cambridge (Ames Street) 3)))
or操作格式:
(or <query1> <query2> ... <queryn>)
(or (supervisor ?x (Bitdiddle Ben))
(supervisor ?x (Hacker Alyssa P)))
;;; 结果:
(or (supervisor (Hacker Alyssa P) (Bitdiddle Ben))
(supervisor (Hacker Alyssa P) (Hacker Alyssa P)))
(or (supervisor (Fect Cy D) (Bitdiddle Ben))
(supervisor (Fect Cy D) (Hacker Alyssa P)))
(or (supervisor (Tweakit Lem E) (Bitdiddle Ben))
(supervisor (Tweakit Lem E) (Hacker Alyssa P)))
(or (supervisor (Reasoner Louis) (Bitdiddle Ben))
(supervisor (Reasoner Louis) (Hacker Alyssa P)))
not操作格式:
(not <query1>)
(and (supervisor ?x (Bitdiddle Ben))
(not (job ?x (computer programmer))))
还有一种形式为lisp-value。如果lisp-value是第一个元素,那第二个元素就是谓词:
(lisp-value <predicate> <arg1> ... <argn>)
例如:找出工资大于30,000美元的工人:
(and (salary ?person ?amount)
(lisp-value > ?amount 30000))
lisp-value应该只用于查询查询语言里没有提供的喉舌。
练习 4.56
- Ben Bitdiddle所有下属的名字和住址。
- 工资比Ben Bitdiddle少的人的工资和Ben Bitdiddle的工资。
- 所有不是计算机分部的人管理的人,以及他们上司的工作。
(and (supervisor ?person (Bitdiddle Ben))
(address ?person ?where))
(and (salary (Bitdiddle Ben) ?number)
(salary ?person ?amount)
(lisp-value < ?amount ?number))
(and (supervisor ?person ?boss)
(not (job ?boss (computer . ?type)))
(job ?boss ?job))
规则
规则(rule)可以用来对查询进行抽象。格式为:
(rule <conclusion> <body>)
例如,定义规则same判断两个变量是否相等,只要是同一个模式变量,就说明相等:
(rule (same ?x ?x))
(rule (lives-near ?person-1 ?person-2)
(and (address ?person-1 (?town . ?rest-1))
(address ?person-2 (?town . ?rest-2))
(not (same ?person-1 ?person-2))))
「住得近」的规则是:检查两个是住在同一个镇里,而且不能是同一个人:
(rule (lives-near ?person-1 ?person-2)
(and (address ?person-1 (?town . ?rest-1))
(address ?person-2 (?town . ?rest-2))
(not (same ?person-1 ?person-2))))
查找Ben Bitdiddle附近的员工:
(lives-near ?x (Bitdiddle Ben)) ;;; result (lives-near (Reasoner Louis) (Bitdiddle Ben)) (lives-near (Aull DeWitt) (Bitdiddle Ben))
查找Ben Bitdiddle附近的程序员:
(and (job ?x (computer programmer))
(lives-near ?x (Bitdiddle Ben)))
「大人物」的规则是:他管的人下面还管着人:
(rule (wheel ?person)
(and (supervisor ?middle-manager ?person)
(supervisor ?x ?middle-manager)))
规则也可以是其他规则的一部分,还可以像递归函数一样定义递归的规则。 例如,一个职员是一个老板的下级,条件是如果这个老板就是他的主管, 或(递归地)这个人的主管是这个老板的下级:
(rule (outranked-by ?staff-person ?boss)
(or (supervisor ?staff-person ?boss)
(and (supervisor ?staff-person ?middle-manager)
(outranked-by ?middle-manager ?boss))))
练习 4.57
定义规,另一个可以替代某人的工作:
- 所有能代替Cy D. Fect的人。
- 所有能代替工资比自己高的人的人,以及这两个人的工资。
(a)
(assert! (rule (replace ?person1 ?person2)
(and (job ?person1 ?job1)
(job ?person2 ?job2)
(or (same ?job1 ?job2)
(can-do-job ?job1 ?job2))
(not (same ?person1 ?person2)))))
(b)
(replace ?p (Fect Cy D))
;;; Query output:
(replace (Bitdiddle Ben) (Fect Cy D))
(replace (Hacker Alyssa P) (Fect Cy D))
(c)
(and (salary ?p1 ?a1)
(salary ?p2 ?a2)
(replace ?p1 ?p2)
(lisp-value > ?a2 ?a1))
;;; Query output:
(and (salary (Aull DeWitt) 25000)
(salary (Warbucks Oliver) 150000)
(replace (Aull DeWitt) (Warbucks Oliver))
(lisp-value > 150000 25000))
(and (salary (Fect Cy D) 35000)
(salary (Hacker Alyssa P) 40000)
(replace (Fect Cy D) (Hacker Alyssa P))
(lisp-value > 40000 35000))
练习 4.58
定论「部门里的大人物」,他在他的部门是最大的:
(assert! (rule (bigshot ?person ?division)
(and (job ?person (?division . ?rest))
(or (not (supervisor ?person ?boss))
(and (supervisor ?person ?boss)
(not (job ?boss (?division . ?r))))))))
;;; Query output:
(bigshot (Warbucks Oliver) administration)
(bigshot (Scrooge Eben) accounting)
(bigshot (Bitdiddle Ben) computer)
练习 4.59
现在有关于会议的断言信息:
;;; 每个部门的信息 (meeting accounting (Monday 9am)) (meeting administration (Monday 10am)) (meeting computer (Wednesday 3pm)) (meeting administration (Friday 1pm)) ;;; 全公司的会议的信息 (meeting whole-company (Wednesday 4pm))
a) 如何查询周五Ben要参加的会议。
b) 根据名字查会议。完成以下填空:
(rule (meeting-time ?person ?day-and-time)
<rule-body>)
c) 根据以上成果,打周三Alyssa要参加的会议。
(a)
(meeting ?dept (Friday . ?t))
(b)
(rule (meeting-time ?person ?day-and-time)
(and (job ?person (?dept . ?r))
(or (meeting ?dept ?day-and-time)
(meeting the-whole-company ?day-and-time))))
(c)
(and (meeting-time (Hacker Alyssa P) (Wednesday . ?time))
(meeting ?dept (Wednesday . ?time)))
练习 4.60
找与指定的人附近的人,可以正常工作:
(lives-near ?person (Hacker Alyssa P))
但为什么要找任意两个附件的人,会有重复的结果?如:
(lives-near ?person-1 ?person-2) ;;; 结果重复: (lives-near (Hacker Alyssa P) (Fect Cy D)) (lives-near (Fect Cy D) (Hacker Alyssa P))
因为不同的顺序都符合条件。
如果按人名排序,就只有一个结果:
(define (person->string person)
(if (null? person)
""
(string-append (symbol->string (car person))
(person->string (cdr person)))))
(define (person>? p1 p2)
(string>? (person->sring p1) (person->string p2)))
(assert! (rule (asy-lives-near ?person1 ?person2)
(and (address ?person1 (?town . ?rest-1))
(address ?person2 (?town . ?rest-2))
(lisp-value person>? ?person1 ?person2))))
将规则看作程序
例子,append操作组合两个表,它的过程定义就包含了对规则的实现:
(define (append x y)
(if (null? x)
y ;; 规则1
(cons (car x)
(append (cdr x) y)))) ;; 规则2
-
空表与
y进行append的结果就是y。 -
如果
v和y进行append的结果是z,那么(cons u v)与y进行append的结果为(cons u z)。
所以,对于以下的关系「x与y的append操作形成了z」:
(append-to-form x y z)
基于以上的append-to-form,可以实现规则1和规则2:
(rule (append-to-form () ?y ?y)) ;; 这里没有规则体,说明y为任何值都成立。
(rule (append-to-form (?u . ?v) ?y (?u . ?z)) ;; ?v 和 ?y 合并为 ?z
(append-to-form ?v ?y ?z)) ;; 如果 ?v ?y 等于 ?z
有了这两条规则,就可以写出查询,去计算两个表的append操作:
;;; Query input: (append-to-form (a b) (c d) ?z) ;;; Query results: (append-to-form (a b) (c d) (a b c d))
还可以用来解决「哪个表append到(a b)可以产生出(a b c d)」这样的问题:
;;; Query input: (append-to-form (a b) ?y (a b c d)) ;;; Query results: (append-to-form (a b) (c d) (a b c d))
还可以穷举出所有append出(a b c d)的组合:
;;; Query input: (append-to-form ?x ?y (a b c d)) ;;; Query results: (append-to-form () (a b c d) (a b c d)) (append-to-form (a) (b c d) (a b c d)) (append-to-form (a b) (c d) (a b c d)) (append-to-form (a b c) (d) (a b c d)) (append-to-form (a b c d) () (a b c d))
练习 4.61
以下的next-to可以打出相邻的元素:
(rule (?x next-to ?y in (?x ?y . ?u)))
(rule (?x next-to ?y in (?v . ?z))
(?x next-to ?y in ?z))
以下查询的结果是什么?
(?x next-to ?y in (1 (2 3) 4)) (?x next-to 1 in (2 1 3 1))
答:
;;; Query input: (?x next-to ?y in (1 (2 3) 4)) ;;; Query output: ((2 3) next-to 4 in (1 (2 3) 4)) (1 next-to (2 3) in (1 (2 3) 4)) ;;; Query input: (?x next-to 1 in (2 1 3 1)) ;;; Query output: (3 next-to 1 in (2 1 3 1)) (2 next-to 1 in (2 1 3 1))
练习 4.62
实现last-pair操作来取得非空表中的最后一个元素。并检查能否正常处理以下问题:
(last-pair (3) ?x) (last-pair (1 2 3) ?x) (last-pair (2 ?x) (3)) (last-pair ?x (3))
(assert! (rule (last-pair (?x) (?x))))
(assert! (rule (last-pair (?u . ?v) (?x))
(last-pair ?v (?x))))
;;; Query input:
(last-pair (3) ?x)
;;; Query output:
(last-pair (3) (3))
;;; Query input:
(last-pair (1 2 3) ?x)
;;; Query output:
(last-pair (1 2 3) (3))
;;; Query input:
(last-pair (2 ?x) (3))
;;; Query output:
(last-pair (2 3) (3))
;;; there is no answer for (last-pair ?x (3))
练习 4.63
根据《创世纪》里的血缘表:
(son Adam Cain) (son Cain Enoch) (son Enoch Irad) (son Irad Mehujael) (son Mehujael Methushael) (son Methushael Lamech) (wife Lamech Ada) (son Ada Jabal) (son Ada Jubal)
构建出一些规则,如:
- 如果S是F的儿子,且F是G的儿子,那么S就是G的孙子。
- 如果W是M的妻子,且S是W的儿子,那么S也是M的儿子。
这样可以找到Cain的孙子,Lamech的儿子,Methushael的孙子。
(assert! (rule (father ?s ?f)
(or (son ?f ?s)
(and (son ?w ?s)
(wife ?f ?w)))))
(assert! (rule (grandson ?g ?s)
(and (father ?s ?f)
(father ?f ?g))))
;;; Query input:
(grandson Cain ?s)
;;; Query output:
(grandson Cain Irad)
;;; Query input:
(father ?s Lamech)
;;; Query output:
(father Jubal Lamech)
(father Jabal Lamech)
;;; Query input:
(grandson Methushael ?s)
;;; Query output:
(grandson Methushael Jubal)
(grandson Methushael Jabal)
查询系统如何工作
实现方案:
- 采用4.3节的amb求值器,实现为一个非确定性程序。
- 借助于流,设法控制搜索。
这里采用的是第二种方案。
模式匹配
「模式匹配器」是一个程序,它检查一个数据是否符合指定的模式。
例如对于指定的数据((a b) c (a b)):
-
匹配模式
(?x c ?x),其中变量?x约束为(a b)。 -
匹配模式
(?x ?y ?z),其中变量?x和?y约束为(a b)、?y约束为c。 -
匹配模式
((?x ?y) c (?x ?y)),其中变量?x约束为a而?y约束为b。 -
不能匹配
(?x a ?y)。
匹配的过程:
- 模式匹配器需要三个参数:模式、数据、栈帧(变量约束的值)。
- 检查数据是否以某种方式与模式匹配。
- 该匹配的方式是否与现有栈帧中的约束相容。
-
返回结果:
- 如果成功,扩充现有的栈帧,作为返回值返回。
- 如果失败,返回匹配失败。
栈帧的流
- 一个查询以一个栈帧流作为输入。
-
对于每个输入栈帧,匹配过程都会扫描数据库里的所有记录。
- 匹配失败的生成指定的失败符号。
- 匹配成功的返回该栈帧的一个扩充。
- 所有的匹配结果集中为一个新的流,通过一个过滤器,删除失败的元素。 生成满足条件的栈帧的流。
- 把每个输入栈帧得到的流合并为一个大的流,就是整个查询的结果。
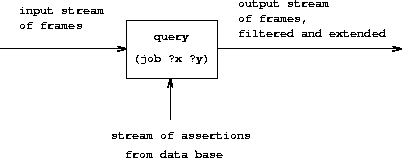
复合查询
(and (can-do-job ?x (computer programmer trainee))
(job ?person ?x))
先找出:
(can-do-job ?x (computer programmer trainee))
这样得到的结果都已经有了对于?x的结束。这样对于其中的每个栈帧,
再找出能够匹配以下条件的:
(job ?person ?x)
这个每个符合的栈帧双可以扩展出对于?person的约束。整个过程的描述如图:
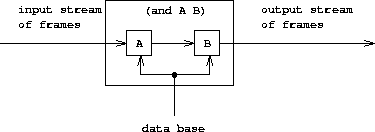
如果复合查询是用or连接的,那么相当于两个流的合并:
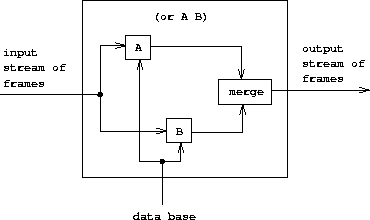
至于not查询,可以把它视为一个过滤器。例如对于以下模式:
(not (job ?x (computer programmer)))
就是要删除流中可以匹配的栈帧。具体到复合查询中:
(and (supervisor ?x ?y)
(not (job ?x (computer programmer))))
第一个查询的结果是带有?x和?y约束的栈帧,而第二个查询要从中过滤掉程序员。
这里也把lisp-value实现为栈帧流上的一个容器。用流里的每个栈帧实例化模式里的变量
,然后对得到的实例化结果应用给定的List谓词,在谓词为假时从流过滤掉相应的栈帧。
合一
合一操作类似于求联立方程:对于两个包含常量和变量的模式, 设法找到让它们相等的变量的值。
例,可以成功合一的例子:
(?x a ?y) (?y ?z a )
以上两个可以合一,生成新的栈帧,其中?x、?y、?z都约束到a。
例,不可以成功合一的例子:
(?x ?y a ) (?x b ?y)
无论?y的值是什么,都无法让两个模式相等。
例,描述合一的过程:
(?x ?x) ((a ?y c) (a b ?z))
以上两个模式可以描述为联立方程:
?x = (a ?y c) ?x = (a b ?z) ;; 可以推导出: (a ?y c) = (a b ?z) ;; 得到 a = a, ?y = b, c = ?z, ;; ?x = (a b c)
从上面的例子中可以看到,合一的最终目标是模式变量都约束到常量。例如,对于:
(?x a) ((b ?y) ?z)
二者合一可以推导出:
?x = (b ?y) a = ?z
虽然这里?x和?y的值还不能确定到常量,但是如果以后有新的结束到?x或?y,
还是有可能配平的。
规则的应用
规则的应用就像是「规则的调用」和「规则的结论」二者进行合一:
(lives-near ?x (Hacker Alyssa P)) ;; 调用规则,有实际参数
(rule (lives-near ?person-1 ?person-2) ;; 该规则的结论
(and (address ?person-1 (?town . ?rest-1))
(address ?person-2 (?town . ?rest-2))
(not (same ?person-1 ?person-2))))
这里参数?person-1得到的实参还是模式变量,但是?person-2得到的是常量
(Hacker Alyssa P)。
应用规则的过程可以总结为:
- 把规则应用和规则的结论作全一,如果成功会返回对于原来栈帧的扩充。
- 用扩充过的栈帧,来求值由规则体形成的查询。
这里可以看到规则的调用就像是函数的调用非常相似,函数的eval-apply调用过程:
- 把过程的形参约束于实参,形成栈帧去扩充原来的过程环境。
- 用扩充后的环境,去求值过程体形成的表达式。
简单查询
之前已经讨论了:
- 在没有规则的情况下,如何求值简单查询。
- 如何应用规则。
现在讨论如何通过使用规则和断言去求值简单查询。
给定一个「查询模式」和一个「栈帧的流」,可以根据流里的每个栈帧生成两个流:
- 使用模式匹配器,用指定的模式与数据库里所有断言做匹配,得到一个扩充栈帧的流。
- 应用所有可能的规则,生成另一个扩充栈帧的流。
这两个流连接到一起产生出新的流,其中包含了与原栈帧相容的, 能满足指定模式的各种方式。将这些流(输入流里每个栈帧都有一个流)组成更大的流, 其中包含了可以从原来输入流中每个栈帧扩充而得到的、与指定模式匹配的所有方式。
查询求值器和驱动循环
和之前语言求值器的eval过程类似,查询语言协调各种匹配操作过程称为qeval。
它以一个「查询」和一个「栈帧的流」作为输入,输出结果是对应输入栈帧扩充的流,
输出的流对应于查询模式的所有成功匹配。
与eval类似,qeval也会对不同的操作类型进行分类指派,如:and、or、not、
lisp-value以及一个针对简单查询的过程。
查询的驱动循环也和之前查询语言的driver-loop过程类似:
-
根据用户输入的查询与空框架的流作为参数调用
qeval,生成所有可能的匹配的流。 - 针对流里的每个栈帧里的值去实例化原来的查询,实例化后得到的流被打印出来。
注意:这里不能用表而是要用可以延时求值流,因为可能会有无穷多个满足查询的值。
驱动循环要处理一种特殊的输入assert!,它用于表示这不是一个查询,而是一个断言。
应该添加到数据库里。如:
(assert! (job (Bitdiddle Ben) (computer wizard)))
(assert! (rule (wheel ?person)
(and (supervisor ?middle-manager ?person)
(supervisor ?x ?middle-manager))))
逻辑程序设计是数理逻辑吗
逻辑程序设计分离了「需要计算什么」和「如何进行计算」两个问题。 它只是数理逻辑中的一个子集:
- 要足够强大到可以描述问题,解决「做什么」的问题。
- 但也不能太强,要给我们留下用过程性的方式定义「怎么做」的方式。
例如:为了查找出所有程序员的上司,可以用两种不同的逻辑查询。
;;; query 1:
(and (job ?x (computer programmer))
(supervisor ?x ?y))
;;; query 2:
(and (supervisor ?x ?y)
(job ?x (computer programmer)))
第一种方式在上司比程序员多的情况下速度更快;第二种方法中, 第一个子句为了生成的每个中间结果(栈帧),要扫描整个数据库。
在查询语句中,程序员可以控制「怎么做」,就样就可以选择用性能好的方式实现。
无穷循环
例子,设计一个婚姻的数据库,增加一个断言:
(assert! (married Minnie Mickey))
然后进行查询:
(married Mickey ?who)
这里得不到答案,因为系统并不知道A与B结婚也代表了B与A结婚。这时如果加入规则:
(assert! (rule (married ?x ?y)
(married ?y ?x)))
然后再查询会进入死循环:
-
规则的结论
(married ?x ?y)成功与查询模式(married Mickey ?who)匹配, 产生一个栈帧:?x约束到Mickey而?y约束到?who。 -
解释器继续执行,在这一个栈帧里求值规则的体
(married ?y ?x),相当于处理(married Minnie Mickey)。 -
现在数据库里得到一个断言:
(married Minnie Mickey)。 -
由于married规则仍然可以应用,所以解释器又去求规则的体,这次规则体等于
(married Mickey ?who)。这样就进入了无穷循环。
与not有关的问题
以4.4.1节的数据库为例,以下两个查询会有不同的结果:
(and (supervisor ?x ?y)
(not (job ?x (computer programmer))))
它选找出与supervisor ?x ?y匹配的条目,然后扣除了所有?x满足
(job ?x (computer programmer))的条目。
(and (not (job ?x (computer programmer)))
(supervisor ?x ?y))
它在一开始排除所有满足(job ?x (computer programmer))的栈帧,返回空的框架流。
然后整个复合查询也将得到空的流。
问题出在对not的解释,实际上希望是not对变量的值进行过滤。
如果not子句作用在一个还有变量没有被约束的框架上(如例子中的?x)就有问题。
同样当lisp-value中的lisp谓词的参数还没有被约束时,也会有问题。
这里的not还有一个问题是它和数理逻辑里的not不同:
- 数理逻辑中,「非P」表示P不为真。
- 查询系统中,「非P」表示P不能由数据库中的内容推导出来。
练习 4.64
把原来的outranked-by规则:
(rule (outranked-by ?staff-person ?boss)
(or (supervisor ?staff-person ?boss)
(and (supervisor ?staff-person ?middle-manager)
(outranked-by ?middle-manager ?boss))))
改成这样:
(rule (outranked-by ?staff-person ?boss)
(or (supervisor ?staff-person ?boss)
(and (outranked-by ?middle-manager ?boss)
(supervisor ?staff-person ?middle-manager))))
这样查找比Ben Bitdiddle级别高的人时:
(outranked-by (Bitdiddle Ben) ?who)
系统以给出答案,但输出以后就死循环了,请解释原因:
查询与规则进行合一以后,会执行:
(outranked-by ?middle-manager ?boss)
这将查询再次查询:
(outranked-by ?staff-person ?boss)
所以是无限循环。
练习 4.65
使用4.4.1 节定义的wheel规则来打出公司里的大人物:
(wheel ?who)
输出里为什么有些记录重复了4次:
;;; Query results: (wheel (Warbucks Oliver)) (wheel (Bitdiddle Ben)) (wheel (Warbucks Oliver)) (wheel (Warbucks Oliver)) (wheel (Warbucks Oliver))
因为在数据库里,Warbucks Oliver手下有四个中层经理。
- Scrooge 管理 Cratchet
- Bitdiddle 管理 Hacker
- Bitdiddle 管理 Fect
- Bitdiddle 管理 Tweakit
练习 4.66
为了找出所有程序员的工资,可以写出:
(sum ?amount
(and (job ?x (computer programmer))
(salary ?x ?amount)))
如何扩展查询器,实现以下的功能,实现类似编程语言中的sun、average的功能:
(accumulation-function <variable>
<query pattern>)
目前的思路是把查询模式传入qeval,产生出一个栈帧的流,再把流送给一个映射函数。
映射函数从每个栈帧中取出指定变量的值。得到的结果值的流再送入一个累积函数。
结合练习 4.65的错误,这个思路有什么问题?如何修正?
If Ben want to get to sum of salary of wheels, he can you this query:
(and (wheel ?who) (salary ?who ?amount))
输出:
(and (wheel (Warbucks Oliver)) (salary (Warbucks Oliver) 150000)) (and (wheel (Warbucks Oliver)) (salary (Warbucks Oliver) 150000)) (and (wheel (Bitdiddle Ben)) (salary (Bitdiddle Ben) 60000)) (and (wheel (Warbucks Oliver)) (salary (Warbucks Oliver) 150000)) (and (wheel (Warbucks Oliver)) (salary (Warbucks Oliver) 150000))
you can see that Warbucks Oliver's salary occurs four times, so in the sum, Warbucks Oliver's salary will be duplicated. Ben can use an unique function to filter the duplication in the amount.
练习 4.67
为了防止练习 4.64中那样简单的无限循环,在系统中增加一个监视器,会跟踪执行历史, 不再重复执行某个正在处理中的查询。
实现这一目标要跟踪执行历史中的哪些信息(如模式和框架)?要做哪些检查?
https://github.com/l0stman/sicp/blob/master/4.67.tex
To detect this kind of loop, we keep track of an already processed simple query in a history. This entry is composed of the query itself and the free variables of the query in the frame it's been evaluated. A free variable here means that the variable is unbound in the frame or the value of the variable is a free variable itself.
We then modify apply-a-rule to check if a simple query has
already been processed with the procedure
already-processed?. This is done by trying to unify in
the current frame the query with a query already processed. If the
free variables of the processed query are still unbound in the
resulting frame, it means that we're processing the same query again.
Thus we have detected a loop. See the file 4.67.query.scm
for the complete implementation.
(define (qeval query frame-stream history)
(let ((qproc (get (type query) 'qeval)))
(if qproc
(qproc (contents query) frame-stream history)
(simple-query query frame-stream history))))
(define (simple-query query-pattern
frame-stream
history)
(stream-flatmap
(lambda (frame)
(stream-append-delayed
(find-assertions query-pattern frame)
(delay (apply-rules query-pattern
frame
history))))
frame-stream))
(define (apply-rules pattern frame history)
(stream-flatmap (lambda (rule)
(apply-a-rule rule
pattern
frame
history))
(fetch-rules pattern frame)))
(define (apply-a-rule rule
query-pattern
query-frame
history)
(let* ((clean-rule (rename-variables-in rule))
(unify-match
(unify-match query-pattern
(conclusion clean-rule)
query-frame)))
(if (or (eq? unify-match 'failed)
(processed-query? query-pattern
unify-match
history))
the-empty-stream
(qeval (rule-body clean-rule)
(singleton-stream unify-match)
(extend-history query-pattern
unify-match
history)))))
(define (processed-query? query frame hist)
(if (empty-history? hist)
#f
(let* ((h (first-history hist))
(unify-match
(unify-match query
(history-query h)
frame)))
(or (and (not (eq? unify-match 'failed))
(still-unbound? (history-freevars h)
unify-match))
(processed-query? query
frame
(rest-history hist))))))
(define (still-unbound? vars frame)
(or (null? vars)
(and (free-var? (car vars) frame)
(still-unbound? (cdr vars) frame))))
(define (free-var? var frame)
(let ((bind (binding-in-frame var frame)))
(or (not bind)
(and (var? (binding-value bind))
(free-var? (binding-value bind) frame)))))
(define empty-history '())
(define (empty-history? h) (eq? h empty-history))
(define (freevars pat result frame)
(cond ((and (var? pat) (free-var? pat frame))
(cons pat result))
((pair? pat)
(freevars (cdr pat)
(freevars (car pat) result)))
(else result)))
(define (make-history query-pattern frame)
(cons query-pattern (freevars query-pattern '() frame)))
(define (history-query h) (car h))
(define (history-freevars h) (cdr h))
(define (extend-history query-pattern frame history)
(cons (make-history query-pattern frame) history))
(define (first-history h) (car h))
(define (rest-history h) (cdr h))
练习 4.68
利用append-to-form实现练习2.18中的reverse操作,用来反转表中元素的顺序。
让规则可以回答(reverse (1 2 3) ?x)或是(reverse ?x (1 2 3))。
rule:
(assert! (rule (reverse () ())))
(assert! (rule (reverse ?x ?y)
(and (append-to-form (?first) ?rest ?x)
(append-to-form ?rev-rest (?first) ?y)
(reverse ?rest ?rev-rest))))
(reverse (1 2 3) ?x) : infinite loop
;;; Query input:
(reverse ?x (1 2 3))
;;; Query output:
(reverse (3 2 1) (1 2 3))
练习 4.69
增强练习 4.63的规则,为祖孙关系增加「重」的关系,如: Jabal和Jubal是Adam的重重重重重孙。
写出一些规则,去确定某个表的最后符号是grandson。再用它描述出规则,
可以推导出规则:
((great . ?rel) ?x ?y)
其中?real是一个以grandson结束的列表。
用一些查询,如((great grandson) ?g ?ggs)和(?relationship Adam Irad)
来验证这些规则。
(rule (end-in-grandson (grandson)))
(rule (end-in-grandson (?x . ?rest))
(end-in-grandson ?rest))
(rule ((grandson) ?x ?y)
(grandson ?x ?y))
(rule ((great . ?rel) ?x ?y)
(and (end-in-grandson ?rel)
(son ?x ?z)
(?rel ?z ?y)))
查询系统的实现
驱动循环和实例化
驱动循环的实现,接收输入、执行操作、再等等下一个输入:
-
query-syntax-process把输入的表达式解析为程序可以处理的形式。 -
assertion-to-be-added?检查输入是规则则或断言,如果是,那说明不是查询操作。 要用add-rule-or-assertion把规则和断言加入系统中。 -
如果是查询操作,
qeval执行查询操作。 -
输出结果前用
contract-question-mark把输出还原为输入的形式。 -
instantiate把表达式实例化,用帧里的值取代变量。
4.4.4.7节中会实现表达式的语法实现。
(define input-prompt ";;; Query input:" )
(define output-prompt ";;; Query results:")
(define (query-driver-loop)
(prompt-for-input input-prompt)
(let ((q (query-syntax-process (read)))) ;; 解析输入的语句
(cond ((assertion-to-be-added? q)
;; 如果是规则或断言,加入到系统中
(add-rule-or-assertion! (add-assertion-body q))
(newline)
(display "Assertion added to data base.")
(query-driver-loop))
(else
;; 如果是查询,
(newline)
(display output-prompt)
(display-stream
(stream-map ;; 处理查询结果的每个元素
(lambda (frame) ;; 如何处理结果流中的每个元素
;; 实例化表达式,用帧里的值取代变量
(instantiate q
frame
(lambda (v f)
;; 把结果还原为输入的形式
(contract-question-mark v))))
;; 执行查询,得到结果流
(qeval q (singleton-stream '()))))
(query-driver-loop)))))
instantiate过程的作用是实体化一个表达式。首先要复制它,
并用指定栈帧里的值取代这一表达式里的变量。
而且栈帧里的值不一定是常量,有可能是另一个变量或表达式,本身也需要被实例化。
当某个变量不能被实例化时,所执行的回调函数由参数unbound-var-handler指定。
(define (instantiate exp frame unbound-var-handler)
(define (copy exp)
(cond ((var? exp)
(let ((binding (binding-in-frame exp frame)))
;; 是否可以绑定变量
(if binding
(copy (binding-value binding)) ;; 绑定变量
(unbound-var-handler exp frame)))) ;; 不可绑定,则执行回调函数
((pair? exp)
(cons (copy (car exp)) (copy (cdr exp))))
(else exp)))
(copy exp))
求值器
qeval是基本求值器。输入是一个查询和一个栈帧的流,返回扩充后的栈帧的流。
它采用get和put分类各种特殊形式,再指派给对应的过程。
无法识别的类型都视为简单查询,由simple-query处理。
(define (qeval query frame-stream)
(let ((qproc (get (type query) 'qeval)))
(if qproc
(qproc (contents query) frame-stream)
(simple-query query frame-stream))))
4.4.4.7节中实现type和contents。
简单查询
simple-query的参数是一个简单查询模式和栈帧的流作为实际参数,
把查询与数据库匹配的方式扩充其中中每个栈帧,再作为返回值:
-
find-assertions尝试匹配模式与数据库里的断言,返回扩充的栈帧流。 -
apply-rules应用所有可能的规则,生成另一个扩充栈帧的流。 -
生成的两个流被
stream-append-delayed组合为一个流,表示即满足指定模式, 又与开始栈帧相容的所有不同方式。 -
stream-flatmap组合起每个输入栈帧而产生的这种结果流, 代表对初始输入流里的各个栈帧进行扩充,产生出与指定模式匹配的所有可能方式。
(define (simple-query query-pattern frame-stream)
(stream-flatmap ;; 合并扩充后的流与初始的流
(lambda (frame)
(stream-append-delayed ;; 合并数据与规则的流
;; 与数据库匹配生成流
(find-assertions query-pattern frame)
;; 应用规则生成的流
(delay (apply-rules query-pattern frame))))
frame-stream))
复合查询
conjoin实现and查询,以「有关的合取项」和一个「栈帧流」作为参数,
返回扩充栈帧的流。参考图示「and查询」。
- 首先处理栈帧流,找出满足第一个合取项的所有可能的扩充栈帧形成的流。
-
使用新的流,递归地把
conjoin应用于这一and查询的剩余部分。
(define (conjoin conjuncts frame-stream)
(if (empty-conjunction? conjuncts)
frame-stream ;; 合取项为空,直接返回原来的流
(conjoin (rest-conjuncts conjuncts)
(qeval (first-conjunct conjuncts)
frame-stream))))
现在实现了and查询,要把它设置到qeval中:
(put 'and 'qeval conjoin)
disjoin实现了or查询,如图示「or查询」。
- 分别计算出or中各个析取项的输出流。
-
使用
interleave-delayed过程把流都归并起来。
(define (disjoin disjuncts frame-stream)
(if (empty-disjunction? disjuncts)
the-empty-stream
(interleave-delayed
(qeval (first-disjunct disjuncts) frame-stream)
(delay (disjoin (rest-disjuncts disjuncts)
frame-stream)))))
(put 'or 'qeval disjoin)
4.4.4.7节会实现合取和析取的语法谓词和选择谓词。
过滤器
negate实现not查询,处理器尝试扩充流里的每个栈帧,检查是否能满足「被否定」
的查询,把不能满足的都加入到返回的流里:
(define (negate operands frame-stream)
(stream-flatmap
(lambda (frame)
(if (stream-null? (qeval (negated-query operands)
(singleton-stream frame)))
(singleton-stream frame)
the-empty-stream))
frame-stream))
(put 'not 'qeval negate)
lisp-value过滤器的实现类似:
- 用流中的每个栈帧去实例化模式里的变量,然后把谓词应用于得到的实例。
- 输入流里让谓词为假的栈帧被过滤掉。
- 如果遇到未约束的变量,结果就是一个错误。
(define (lisp-value call frame-stream)
(stream-flatmap
(lambda (frame)
(if (execute
(instantiate
call
frame
(lambda (v f)
(error "Unknown pat var -- LISP-VALUE" v))))
(singleton-stream frame)
the-empty-stream))
frame-stream))
(put 'lisp-value 'qeval lisp-value)
execute把谓词应用于对应的参数,必须求值谓词表达式,但是不能对参数求值,
因为它们已经是实际参数了,而不是表达式。
注意execute是利用原生Lisp系统里的eval和apply实现的:
(define (execute exp)
(apply (eval (predicate exp) user-initial-environment)
(args exp)))
特殊形式always-true是为了描述一种永远能满足的查询,简单地返回输入流。
它被用于4.4.4.7节里的选择函数,处理那些没有规则体的规则(即永远能被满足的规则)
:
(define (always-true ignore frame-stream) frame-stream) (put 'always-true 'qeval always-true)
4.4.4.7节里实现not和lisp-value的语法规则和选择函数。
通过模式匹配找出断言
find-assertions以一个模式和一个栈帧作为参数,根据模式与数据库的匹配,
输出扩充后的流。
因为检查数据库中每个一个断言效率太低,这里用fetch-assertions(4.4.5节实现)
过滤掉数据库中大多数的断言。
(define (find-assertions pattern frame)
(stream-flatmap (lambda (datum)
(check-an-assertion datum pattern frame))
(fetch-assertions pattern frame)))
check-an-assertion检查断言与模式是否匹配,成功就返回只有一个扩充栈帧的流,
失败则返回the-empty-stream:
(define (check-an-assertion assertion query-pat query-frame)
(let ((match-result
(pattern-match query-pat assertion query-frame)))
(if (eq? match-result 'failed)
the-empty-stream
(singleton-stream match-result))))
pattern-match实现了基本模式匹配器,它返回栈帧的一个扩充或是失败符号failed。
工作过程就是对照着模式一个一个元素地检查数据,同时积累起各个模式的约束变量。
(define (pattern-match pat dat frame)
(cond ((eq? frame 'failed) 'failed) ;; 栈帧为失败
;; 模式与数据相同,返回栈帧
((equal? pat dat) frame)
;; 模式是变量,把变量与数据的约束加入到栈帧里
((var? pat) (extend-if-consistent pat dat frame))
;; 如果模式和数据都是序对,递归匹配模式的car和数据的cdr
((and (pair? pat) (pair? dat))
(pattern-match (cdr pat)
(cdr dat)
(pattern-match (car pat)
(car dat)
frame)))
(else 'failed))) ;; 无法匹配
扩充栈帧的操作就是在其中加入新的约束。条件是新的约束要和现有的约束相容:
;; 只有当值为常量时,才把值与变量绑定到栈帧中
(define (extend-if-consistent var dat frame)
(let ((binding (binding-in-frame var frame)))
(if binding
;; 如果已经绑定变量,检查新的值是否已经有的值一样
(pattern-match (binding-value binding) dat frame)
;; 还没有绑定这个变量,就把这个变量加进去
(extend var dat frame))))
如果框架里的值是在合一过程中保存的,那也有可能绑定的是变量(参考4.4.4.4节)。
在递归的过程中,新值的匹配可能还会增加:
-
原来的栈帧中,
?x约束为(f ?y)而?y没有约束。 -
现在要扩展新的约束
?x为(f b)。 -
这样就要把原来的
(f ?y)与(f b)匹配,所以?y与b的约束加入框架。
注意在这个过程中,已经有的约束不会修改,也不会为一个变量保存多个约束, 4.4.4.8节中会有更多的细节。
具有带点尾部的模式
带点号的变量匹配表中的多个元素,实现方式是不把下一个项作为表里的下一个元素
(一个cons的car,其cdr将是这个表的其他部分),而是直接作为这个表的cdr。
例:
对于模式:
(computer ?type)
由read产生的表结构相当于以下表达式的结构:
(cons 'computer (cons '?type '()))
而对于带点号的模式:
(computer . ?type)
相当于以下的结构:
(cons 'computer '?type)
规则和合一
apply-rules把模式应用到规则中去:
-
fetch-rules找出当前模式可能用到的规则,作为流输出。 -
stream-flatmap把在流中的每个规则作为参数调用apply-a-rule应用该规则。
(define (apply-rules pattern frame)
(stream-flatmap (lambda (rule)
(apply-a-rule rule pattern frame))
(fetch-rules pattern frame)))
apply-a-rule以4.4.2节中的原则实现规则的应用,注意为了防止重名,
要对所有的变量重命名:
(define (apply-a-rule rule query-pattern query-frame)
(let ((clean-rule (rename-variables-in rule)))
(let ((unify-result
(unify-match query-pattern
(conclusion clean-rule)
query-frame)))
(if (eq? unify-result 'failed)
the-empty-stream
(qeval (rule-body clean-rule)
(singleton-stream unify-result))))))
4.4.4.7节中详细定义rule-body和conclusion。
重命名变量时把变量名和规则名连接起来。比如,规则应用标识为7,则规则里的变量?x
就是?x-7:
(define (rename-variables-in rule)
(let ((rule-application-id (new-rule-application-id)))
(define (tree-walk exp)
(cond ((var? exp)
(make-new-variable exp rule-application-id))
((pair? exp)
(cons (tree-walk (car exp))
(tree-walk (cdr exp))))
(else exp)))
(tree-walk rule)))
4.4.4.7节里定义具体的make-new-variable和new-rule-application-id。
合一过程unify-match的参数是两个模式加上一个栈帧,返回扩充后的栈帧或是失败符号
failed。实现代码与模式匹配器类似,但它是对称的,因为匹配的两边都会有变量。
unify-match和pattern-match基本一样,就多处理右边对象也是变量一行代码
。
(define (unify-match p1 p2 frame)
(cond ((eq? frame 'failed) 'failed)
((equal? p1 p2) frame)
((var? p1) (extend-if-possible p1 p2 frame))
((var? p2) (extend-if-possible p2 p1 frame)) ;; 处理右边也是变量
((and (pair? p1) (pair? p2))
(unify-match (cdr p1)
(cdr p2)
(unify-match (car p1)
(car p2)
frame)))
(else 'failed)))
合一过程与模式匹配类似,新扩充的约束要和现有的约束相容才能进行扩充。
extend-if-possible和之前的extend-if-consistent相似,区别在于增加了两处检查:
-
有新的变量
A要约束到值B时,如果B也是一个变量,要检查B有没有约束:-
如果有,
A也约束到B约束的常量。 - 如果二者都没有约束,其中任意一个可以约束到另一个。
-
如果有,
-
当一个变量约束到一个模式,而模式里又包含这个变量。
- 当两个模式重复出现变量的时候可能出现这种情,由于不存在这种方程的一般性解法, 所以我们的系统拒绝这种约束(详细讨论略)。
-
另一种情况变量与自身的匹配是可解的,如
(x x)与(y y)的合一, 可以通过unify-match里的equal?子句检查。
(define (extend-if-possible var val frame)
(let ((binding (binding-in-frame var frame)))
(cond (binding
(unify-match
(binding-value binding) val frame))
((var? val) ; ***
(let ((binding (binding-in-frame val frame)))
(if binding
(unify-match
var (binding-value binding) frame)
(extend var val frame))))
((depends-on? val var frame) ; ***
'failed)
(else (extend var val frame)))))
depends-on?是一个谓词,检查某模式变量的值的表达式是否依赖于这个变量。
检查要在当前的栈帧做,因为在这个表达式里可能包含某个变量的出现,
而这个变量的值依赖于我们要检查的变量。
depends-on?的结构是一个简单的递归树遍历,其中可能需要将一些变量换成相应的值。
(define (depends-on? exp var frame)
(define (tree-walk e)
(cond ((var? e)
(if (equal? var e)
true
(let ((b (binding-in-frame e frame)))
(if b
(tree-walk (binding-value b))
false))))
((pair? e)
(or (tree-walk (car e))
(tree-walk (cdr e))))
(else false)))
(tree-walk exp))
数据库的维护
为了实现索引,把car部分是常量符号的所有断言建立索引表格。当模式的car也是常量符号 ,就只在索引值一样的范围内查找。利用栈帧里绑定的约束,当模式里的变量确定为常量时 ,也可以缩小到只查相同索引的范围。
本系统里并没有把「利用car,只处理常量符号的情况」写死到程序里, 而是通过谓词和选择程序实现。
(define THE-ASSERTIONS the-empty-stream) ;; 一开始没有数据,流是空的
(define (get-all-assertions) THE-ASSERTIONS) ;; 取得全库的数据
(define (get-indexed-assertions pattern) ;; 根据模式取得主键
(get-stream (index-key-of pattern) 'assertion-stream))
(define (fetch-assertions pattern frame)
(if (use-index? pattern)
(get-indexed-assertions pattern) ;; 可以索引,只查符合的子集
(get-all-assertions))) ;; 不用索引,要查全库
get-stream到表格里找到相应的流,如果没有就返回空的流:
(define (get-stream key1 key2)
(let ((s (get key1 key2)))
(if s s the-empty-stream)))
规则也可以用car部分作为索引,而且由于规则结论可以是任意模式,所以变量也可以索引
。car出来为常量的模式可以和结论部分具有同样car的规则匹配,
还可以和结论部分以变量开始的规则匹配。这样,如果模式的car为常量,
在提取有可能与它匹配的规则时,不但要提取所有结论部分具有同样car的规则,
还要取出结论部分以变量开关的规则。
为此,可以把所有的结论部分以变量开始的规则作为一个单独的流,
以?作为索引保存在表里:
(define THE-RULES the-empty-stream)
(define (get-all-rules) THE-RULES)
(define (get-indexed-rules pattern)
(stream-append
(get-stream (index-key-of pattern) 'rule-stream) ;; 用常量索引的规则
(get-stream '? 'rule-stream))) ;; 用变量索引的规则
(define (fetch-rules pattern frame)
(if (use-index? pattern)
(get-indexed-rules pattern)
(get-all-rules)))
在驱动循环里有用到add-rule-or-assertion!,它把断言和规则加入到数据库里。
它把不但把规则和断言加到数据库的流中,还要加到索引里:
(define (add-rule-or-assertion! assertion)
(if (rule? assertion)
(add-rule! assertion)
(add-assertion! assertion)))
(define (add-assertion! assertion)
(store-assertion-in-index assertion)
(let ((old-assertions THE-ASSERTIONS))
(set! THE-ASSERTIONS
(cons-stream assertion old-assertions))
'ok))
(define (add-rule! rule)
(store-rule-in-index rule)
(let ((old-rules THE-RULES))
(set! THE-RULES (cons-stream rule old-rules))
'ok))
保存前要检查是否可以被索引,如果可以,就存入适当的流:
(define (store-assertion-in-index assertion)
(if (indexable? assertion)
(let ((key (index-key-of assertion)))
(let ((current-assertion-stream
(get-stream key 'assertion-stream)))
(put key
'assertion-stream
(cons-stream assertion
current-assertion-stream))))))
(define (store-rule-in-index rule)
(let ((pattern (conclusion rule)))
(if (indexable? pattern)
(let ((key (index-key-of pattern)))
(let ((current-rule-stream
(get-stream key 'rule-stream)))
(put key
'rule-stream
(cons-stream rule
current-rule-stream)))))))
索引的定义:如果一个模式(断言或规则的结论部分),是以变量或常量符号开始的, 它就可以被存入表格里:
(define (indexable? pat)
(or (constant-symbol? (car pat))
(var? (car pat))))
把模式保存到表格里的键或是?,或是作为该模式开始的那个符号变量:
(define (index-key-of pat)
(let ((key (car pat)))
(if (var? key) '? key)))
如果模式以符号常量开始,该常量就被用于索引,
(define (use-index? pat) (constant-symbol? (car pat)))
练习 4.70
add-assertion!和add-rule!里的let约束起什么作用?
结合3.5.2节里有关ones的无穷流定义:
(define ones (cons-stream 1 ones))
以下版本的实现有什么错:
(define (add-assertion! assertion)
(store-assertion-in-index assertion)
(set! THE-ASSERTIONS
(cons-stream assertion THE-ASSERTIONS))
'ok)
Since the second argument of cons-stream is delayed, we
need to bind the old value to a variable otherwise it will be forever
lost. The new definition just define THE-ASSERTIONS as circular stream.
Because we use:
(cons-stream assertion THE-ASSERTION)
so THE-ASSERTIONS will not be evaluated,
(set! THE-ASSERTION (cons-stream assertion THE-ASSERTIONS))
will make THE-ASSERTION in the stream point to itself.
so if we use THE-ASSERTIONS, it will lead to infinite loop.
流操作
有一些常用的流操作并没有在第三章介绍。
stream-append-delayed和interleave-delayed是stream-append(3.5.3节)和
interleave(3.5.4节)的延时版本。
(define (stream-append-delayed s1 delayed-s2)
(if (stream-null? s1)
(force delayed-s2)
(cons-stream
(stream-car s1)
(stream-append-delayed (stream-cdr s1) delayed-s2))))
(define (interleave-delayed s1 delayed-s2)
(if (stream-null? s1)
(force delayed-s2)
(cons-stream
(stream-car s1)
(interleave-delayed (force delayed-s2)
(delay (stream-cdr s1))))))
在这个系统里经常用到stream-flatmap把操作过程映射到栈帧流上,它相当于是2.2.3节
flat-map过程的流版本,而且stream-flatmap是采用交错的方式累积起各个流。
(define (stream-flatmap proc s)
(flatten-stream (stream-map proc s)))
(define (flatten-stream stream)
(if (stream-null? stream)
the-empty-stream
(interleave-delayed
(stream-car stream)
(delay (flatten-stream (stream-cdr stream))))))
还有以下过程用来生成只有一个元素的流:
(define (singleton-stream x) (cons-stream x the-empty-stream))
查询的语法过程
qeval里使用的type和contents过程的实现,类似2.4.2节的type-tag和contents
:
(define (type exp)
(if (pair? exp)
(car exp)
(error "Unknown expression TYPE" exp)))
(define (contents exp)
(if (pair? exp)
(cdr exp)
(error "Unknown expression CONTENTS" exp)))
驱动循环里关于断言的操作:
(define (assertion-to-be-added? exp) (eq? (type exp) 'assert!)) (define (add-assertion-body exp) (car (contents exp)))
几个特殊操作形式的语法定义:
;; and (define (empty-conjunction? exps) (null? exps)) (define (first-conjunct exps) (car exps)) (define (rest-conjuncts exps) (cdr exps)) ;; or (define (empty-disjunction? exps) (null? exps)) (define (first-disjunct exps) (car exps)) (define (rest-disjuncts exps) (cdr exps)) ;; not (define (negated-query exps) (car exps)) ;; lisp-value (define (predicate exps) (car exps)) (define (args exps) (cdr exps))
规则的语法形式定义:
(define (rule? statement)
(tagged-list? statement 'rule))
(define (conclusion rule) (cadr rule))
(define (rule-body rule)
(if (null? (cddr rule))
'(always-true)
(caddr rule)))
处理查询表达式语法的过程query-syntax-process对变量做出变换,
把?symbol变为(? symbol)。
如:
(job ?x ?y)
变为:
(job (? x) (? y))
这样的好处是把变量符号改为一个表,这样只要检查car是不是?就可以知道是不是变量,
而不用解析字符串。实现逻辑如下:
(define (query-syntax-process exp)
(map-over-symbols expand-question-mark exp))
(define (map-over-symbols proc exp)
(cond ((pair? exp)
(cons (map-over-symbols proc (car exp))
(map-over-symbols proc (cdr exp))))
((symbol? exp) (proc exp))
(else exp)))
(define (expand-question-mark symbol)
(let ((chars (symbol->string symbol)))
(if (string=? (substring chars 0 1) "?")
(list '?
(string->symbol
(substring chars 1 (string-length chars))))
symbol)))
这样处理后,变量都变成了表,而常量还是符号:
(define (var? exp) (tagged-list? exp '?)) (define (constant-symbol? exp) (symbol? exp))
构造名称唯一的变量时,以规则加序号,每次规则应用时加1:
(define rule-counter 0) (define (new-rule-application-id) (set! rule-counter (+ 1 rule-counter)) rule-counter) (define (make-new-variable var rule-application-id) (cons '? (cons rule-application-id (cdr var))))
驱动循环中在打印结果前,要把未约束的模式变换回打印用的正确形式:
(define (contract-question-mark variable)
(string->symbol
(string-append "?"
(if (number? (cadr variable))
(string-append (symbol->string (caddr variable))
"-"
(number->string (cadr variable)))
(symbol->string (cadr variable))))))
栈帧和约束
每个约束都是变量与值的序对:
(define (make-binding variable value) (cons variable value)) (define (binding-variable binding) (car binding)) (define (binding-value binding) (cdr binding)) (define (binding-in-frame variable frame) (assoc variable frame)) (define (extend variable value frame) (cons (make-binding variable value) frame))
练习 4.71
为什么4.4.4.2节里的simple-query和disjoin过程显式地用到delay,而不是用:
(define (simple-query query-pattern frame-stream)
(stream-flatmap
(lambda (frame)
(stream-append (find-assertions query-pattern frame)
(apply-rules query-pattern frame)))
frame-stream))
(define (disjoin disjuncts frame-stream)
(if (empty-disjunction? disjuncts)
the-empty-stream
(interleave
(qeval (first-disjunct disjuncts) frame-stream)
(disjoin (rest-disjuncts disjuncts) frame-stream))))
This will postpone some infinite loop. for example:
(assert! (married Minnie Mickey))
(assert! (rule (married ?x ?y)
(married ?y ?x)))
(married Mickey ?who)
if we don't use delay, there is no answer to display. but if we use it, we can get:
;;; Query output: (married Mickey Minnie) (married Mickey Minnie) (married Mickey Minnie) ....
this is better than nothing. the reason of this difference is that in this example
(apply-rules query-pattern frame)
will lead to infinite loop, if we delay it, we still can get some meaningful answers.
练习 4.72
为什么disjoin和stream-flatmap要以交错地方式合并流?
The reason is same to why we use interleave in 3.5.3, it's convenient to display infinite stream.
练习 4.73
为什么flatten-stream显式地使用了delay?下面的代码有什么错误:
同4.71。
练习 4.74
negate、lisp-value、find-assertions里,很多时候都生成空流或单元素的流。
这样是否用用不差使用交错,可以用更加简洁的stream-flatmap版本。
a) 完成以下填空:
(define (simple-stream-flatmap proc s)
(simple-flatten (stream-map proc s)))
(define (simple-flatten stream)
(stream-map <??>
(stream-filter <??> stream)))
b) 这样会改变系统原来的行为么?
(a)
(define (simple-flatten stream)
(stream-map stream-car
(stream-filter (lambda (s) (not (stream-null? s))) stream)))
(b)
no. the order of stream will not change the result.
This change should be opaque to the query system's behavior since we just changed an implementation, the result remains the same.
练习 4.75 唯一查询
增加一种称为unique的特殊形式,当数据库里恰好只有一条满足的条目时成功。如:
因为只有Ben是系统中唯一的计算机大师,所以只返回一条记录:
(unique (job ?x (computer wizard))) ;; return (unique (job (Bitdiddle Ben) (computer wizard)))
程序员有多个,所以以下查询输出为空:
(unique (job ?x (computer programmer)))
以下查询应该输出所有只有一个人正在做的工作:
(and (job ?x ?j) (unique (job ?anyone ?j)))
unique的工作有两部分:首先写出处理这一特殊形式的过程,然后在qeval中分派。
分派的工作,只要在type (car)时返回的符号是unique时,就分派到指定过程:
(put 'unique 'qeval uniquely-asserted)
uniquely-asserted的实现要在相应unique查询的contents (cdr)部分和
一个栈帧流作为输入。针对流里的每个栈帧都用qeval找出满足指定查询的扩充栈帧流。
所有包含多个条目的流都应该丢弃,接下的流累积到一个流里用为结果,
和not的过滤方式类似。
实现这一操作,并找出所有只有一个上级的人。
;; add those code
(define (uniquely-asserted pattern frame-stream)
(stream-flatmap
(lambda (frame)
(let ((stream (qeval (negated-query pattern)
(singleton-stream frame))))
(if (singleton-stream? stream)
stream
the-empty-stream)))
frame-stream))
(put 'unique 'qeval uniquely-asserted)
(define (singleton-stream? s)
(and (not (stream-null? s))
(stream-null? (stream-cdr s))))
;;; Query input:
(and (supervisor ?person ?boss) (unique (supervisor ?other ?boss)))
;;; Query output:
(and (supervisor (Cratchet Robert) (Scrooge Eben))
(unique (supervisor (Cratchet Robert) (Scrooge Eben))))
(and (supervisor (Reasoner Louis) (Hacker Alyssa P))
(unique (supervisor (Reasoner Louis) (Hacker Alyssa P))))
练习 4.76 优化and查询效率
图4-5所展示的用一系列查询组合实现方式效率较低,处理第二个查询时要针对第一个查询 的所有输出栈帧扫描整个数据库。
另一个方式是分别处理两个子句,检查两个流里所有的输出栈帧对偶是否兼容。 这个操作很像合一,请实现这个方式。
(define (first-binding frame) (car frame))
(define (rest-bindings frame) (cdr frame))
(define (empty-frame? frame) (null? frame))
(define (unify-if-possible var val frame)
(let ((b (binding-in-frame var frame)))
(cond ((not b) (extend var val frame))
((equal? (binding-value b) val) frame)
((var? val)
(unify-if-possible val
(binding-value b)
frame))
(else 'failed))))
(define (unify-frames f1 f2)
(cond ((empty-frame? f1) f2)
((eq? f2 'failed) 'failed)
(else
(let ((b (first-binding f1)))
(unify-frames
(rest-bindings f1)
(unify-if-possible (binding-variable b)
(binding-value b)
f2))))))
(define (unify-frame-streams fs1 fs2)
(stream-flatmap
(lambda (f1)
(stream-filter
(lambda (f) (not (eq? f 'failed)))
(stream-map (lambda (f2) (unify-frames f1 f2))
fs2)))
fs1))
(define (conjoin conjuncts frame-stream)
(let loop ((conjuncts conjuncts)
(res frame-stream))
(if (empty-conjuction? conjuncts)
res
(loop (rest-conjuncts conjuncts)
(unify-frame-streams
res
(qeval (first-conjunct conjuncts)
frame-stream))))))
(put 'and 'qeval conjoin)
练习 4.77 过滤器与未约束变量
当过滤器not和lisp-value作用于包含未约束变量的框架时,可能会引发错误。
一个可行的方案是增加一个「允诺」的机制,先延迟执行,等变量都绑定再返回。 最后执行的时机可以是等所有其他操作都完成了再去执行过程,但更好的方式是 尽量及时地做出过滤。
This time, we could also append filters to the bindings in the frame.
A second argument which represents a list of filters could be passed
to make-frame.
(define (make-frame binds . rest) (list binds (if (null? rest) rest (car rest)))) (define (frame-binds frame) (car frame)) (define (frame-filters frame) (cadr frame)) (define (binding-in-frame var frame) (assoc var (frame-binds frame)))
Since we want to delay the evaluation of a query untill all the variables are bound in a given frame, we define some helper procedures first.
(define (free-var? var frame)
(let ((bind (binding-in-frame var frame)))
(or (not bind)
(and (var? (binding-value bind))
(free-var? (binding-value bind) frame)))))
(define (free-vars pat frame)
(let loop ((pat pat) (result '()))
(cond ((and (var? pat) (free-var? pat frame))
(cons pat result))
((pair? pat)
(loop (cdr pat)
(loop (car pat) result)))
(else result))))
(define (all-bound? vars frame)
(let loop ((vars vars))
(or (null? vars)
(and (binding-in-frame (car vars) frame)
(loop (cdr vars))))))
A filter is a data structure that contains two procedures that take a
frame as argument. The first one is a predicate that tests if we can
apply the filter to a given frame and the second one tests if the
frame passes the filter or not. If it's not the case we return the
symbol failed.
(define (make-filter query frame pred?)
(let ((vars (free-vars query frame)))
(cons (lambda (frame) (all-bound? vars frame))
pred?)))
(define (filter-test filter) (car filter))
(define (filter-pred filter) (cdr filter))
(define (add-filter frame query pred?)
(let ((filter (make-filter query frame pred?)))
(cond (((filter-test filter) frame)
(if ((filter-pred filter) frame)
frame
'failed))
(else
(make-frame (frame-binds frame)
(append (frame-filters frame)
(list filter)))))))
The following procedure divides the filters of a given frame into two sets. The first one represents those that could be applied to the frame and the second one those that should be delayed.
(define (select-filters frame)
(let loop ((filters (frame-filters frame))
(valids '())
(invalids '()))
(if (null? filters)
(cons valids invalids)
(let ((valid? (filter-test (car filters))))
(if (valid? frame)
(loop (cdr filters)
(cons (car filters) valids)
invalids)
(loop (cdr filters)
valids
(cons (car filters) invalids)))))))
We define extend as usual except that all the filters that
could be applied to the resulting frame take effect immediately.
(define (extend var val frame)
(let* ((frame1 (make-frame
(cons (make-binding var val)
(frame-binds frame))
(frame-filters frame)))
(selected-filters (select-filters frame1)))
(let loop ((filters (car selected-filters))
(rest-filters (cdr selected-filters)))
(if (null? filters)
(make-frame (frame-binds frame1)
rest-filters)
(let ((filter? (filter-pred (car filters))))
(if (filter? frame1)
(loop (cdr filters) rest-filters)
'failed))))))
We use a modified query-driver-loop since before printing
the results, we need to apply all the remaining filters to a given
frame.
(define (force-filters frame)
(let loop ((filters (frame-filters frame)))
(if (null? filters)
(make-frame (frame-binds frame))
(let ((filter? (filter-pred (car filters))))
(if (filter? frame)
(loop (cdr filters))
'failed)))))
(define (query-driver-loop)
(prompt-for-input input-prompt)
(let ((q (query-syntax-process (read))))
(cond ((assertion-to-be-added? q)
(add-rule-or-assertion!
(add-assertion-body q))
(display "Assertion added to data base.")
(newline)
(query-driver-loop))
(else
(display output-prompt)
(newline)
(display-stream
(stream-flatmap
(lambda (frame)
(let ((frame (force-filters frame)))
(if (eq? frame 'failed)
the-empty-stream
(singleton-stream
(instantiate* q
frame
(lambda (v f)
(contract-question-mark v)))))))
(qeval q (singleton-stream (make-frame '())))))
(query-driver-loop)))))
The implementations of negate and lisp-value
are now straightforward.
(define (stream-map-and-filter proc stream)
(stream-filter (lambda (frame)
(not (eq? 'failed frame)))
(stream-map proc stream)))
(define (negate operands frame-stream)
(stream-map-and-filter
(lambda (frame)
(let ((query (negated-query operands)))
(add-filter frame
query
(lambda (frame1)
(stream-null?
(qeval query
(singleton-stream frame1)))))))
frame-stream))
(put 'not 'qeval negate)
(define (lisp-value call frame-stream)
(stream-map-and-filter
(lambda (frame)
(add-filter call
frame
(lambda (frame1)
(execute
(instantiate*
call
frame1
(lambda (v f)
(error "Unknown pat var -- LISP-VALUE" v)))))))
frame-stream))
(put 'lisp-value 'qeval lisp-value)
练习 4.78
这里是用流过程实现的查询语言,尝试用4.3节的求值器实重新现为非确定性程序。
每个查询产生一个回答,而不是所有的回答都是一个流,但可以通过输入try-again
得到更多回答。可以看出,这一节构造出来的大部分机制都被非确定性搜索和回溯所概括了
。而且从行为上看,新的实现和本节的语言有一些小差异,举例说明差异在哪里。
We're embedding the query evaluator inside the amb evaluator. This
time, we don't explicitly define a driver loop. Instead, we define
the procedures assert! and query in order to
interact with the query database. The result of a query is displayed
one at a time and we need to type try-again in order to
see the next solution if any.
Since the amb evaluator is searching for solutions in deep-first
order, we need to ``interleave'' the search results in the case of an
or query. Here we use, the ramb operator
defined in Exercise 4.50 instead of amb.
The negate operator's implementation also needs to be
pointed to. Since we need to test if a query has no solution in order
to keep the frame otherwise we search for the next solution, we
introduce a new syntax
if-fail-only <test> <result>
to the amb evaluator. If the evaluation of <test> fails, then we
return the evaluation of <result>, otherwise we backtrack.
Here's the implementation
(define (if-fail-only? exp)
(tagged-list? exp 'if-fail-only))
(define if-fail-only-test cadr)
(define if-fail-only-result caddr)
(define (analyze-if-fail-only exp)
(let ((test-proc (analyze (if-fail-only-test exp)))
(res-proc (analyze (if-fail-only-result exp))))
(lambda (env succeed fail)
(test-proc env
(lambda (test fail2)
(fail))
(lambda ()
(res-proc env
(lambda (res fail2)
(succeed res fail2))
fail))))))
For the complete implementation of the query evaluator, see the file
amb-query.scm.
With our new implementation, if we enter an infinite loop, the evaluator won't be stuck as in the implementation using a stream. Instead, we will print the same result over and over again. Consider the following example:
;;; Amb-Eval input:
(assert! '(married sarah michael))
;;; Starting a new problem
Assertion added to data base
;;; Amb-Eval value:
ok
;;; Amb-Eval input:
(assert! '(rule (married ?x ?y)
(married ?y ?x)))
;;; Starting a new problem
Assertion added to data base
;;; Amb-Eval value:
ok
;;; Amb-Eval input:
(query '(married ?x ?y))
;;; Starting a new problem
(married sarah michael)
;;; Amb-Eval value:
ok
;;; Amb-Eval input:
try-again
(married michael sarah)
;;; Amb-Eval value:
ok
;;; Amb-Eval input:
try-again
(married sarah michael)
;;; Amb-Eval value:
ok
;;; Amb-Eval input:
try-again
(married michael sarah)
;;; Amb-Eval value:
ok
;;; Amb-Eval input:
练习 4.79 变量作用域
本节是通过重命名来解决不同变量重名问题的,请改为使用局部环境的方式, 构建自己的环境。
(略)